Réalisation en Guides d'Ondes Numériques Stables d'un

Modèle Acoustique Réaliste pour la

Simulation en Temps-Réel d'Instruments à Vent

Rémi Mignot

Ce travail a pour objet l'étude de la modélisation physique des tubes acoustiques à section variable avec pertes, par l'approche des Guides d'Ondes (cf. eg. [Smith87]). Le but est la simulation numérique dans le domaine temporel pour la synthèse sonore d'instruments à vent. Cette thèse poursuit des travaux précédents sur le domaine (cf. eg. [Matignon95]), mais en utilisant un modèle acoustique unidimensionnel plus réaliste : le modèle de Webster-Lokshin (cf. [Hélie03]). Ce modèle décrit la propagation des ondes longitudinales dans les tubes acoustiques axi-symétriques avec une section variable, des pertes visco-thermiques, et avec une hypothèse faible sur la symétrie des isobares (ni planes, ni sphériques). L'équation de Webster-Lokshin caractérise la pression acoustique, elle est donnée dans le domaine de Laplace par

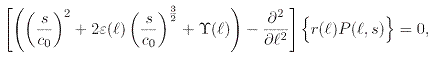
où l est l'abscisse curviligne à la paroi, r(l) est le rayon, P(l,s) est la pression acoustique, ε(l) représente les pertes visco-thermiques et (l) = r''(l)/r(l) est la courbure.

Pour l'utilisation de l'approche des Guides d'Ondes : premièrement nous définissons le changement de variables p^±(l,s) := 1/2 (P(l,s) ± Zc U(l,s)), où U est le débit acoustique et Zc est une impédance caractéristique arbitraire. Puis, nous considérons un tronçon de tube de longueur L, avec des paramètres de pertes ε et de courbure constants. Enfin, la résolution d’équation de Webster-Lokshin et de l'équation d'Euler pour un tronçon de tube aboutit à un système sous forme de quadripôle pour lequel les entrées sont les ondes entrantes (et) et les sorties les ondes sortantes (et).

Ce quadripôle est à l'origine constitué de 4 fonctions de transfert qui imitent les effets acoustiques globaux. Cependant dans Ref. [A3] l'analyse détaillée des effets élémentaires internes au tronçons mène à la nouvelle structure de la figure 1. Dans cette décomposition, les effets de la géométrie du tube sont isolés les uns des autres.

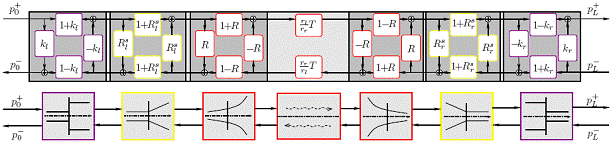
FIGURE 1 – Séparation des effets de la géométrie du tube

Pour x{l,r} (indices représentant les extrémités gauche et droite (left et right)), les éléments de la structure sont donnés par:

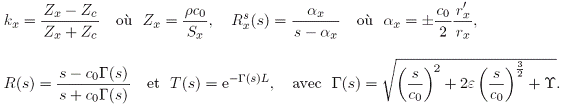
La structure est interprétée de la manière suivante : les coefficients kx représentent les réflexions aux extrémités dues aux discontinuités de section de tube (). (s) sont les fonctions de réflexions dues aux discontinuités de pente (). R(s) est la fonction de réflexion due au changement de courbure et de coefficient de pertes et T(s) représente le retard et l'effet de la propagation d'ondes à travers le tube.

Pour construire un résonateur complet, plusieurs quadripôles modélisant chacun un tronçon de tube sont connectés les uns aux autres. En considérant des cas particuliers de connexion de tronçons de tube, cette structure mène à la structure de Kelly-Lochbaum d'un réseau de cylindres (cf. eg. [Markel73]), de cônes (cf. eg. [Välimäki95]) ou de tube évasés avec pertes. Ce dernier cas (cf. Ref. [C2]) permet d'approximer le profil original du tube par une fonction du rayon r(l) de classe C¹ (ce qui signifie la continuité de rayon et de pente aux jonctions). Grâce à cette amélioration, les pavillons des cuivres (trompettes, trombones, etc...) peuvent être facilement construits avec seulement 4 tronçons de tube, et simulés par une structure de Kelly-Lochbaum, ce qui réduit le coût de calcul.

Cependant, à cause de la racine carré dans l'expression de (s), les fonctions de transfert R(s) et T(s) sont irrationnelles. Elles appartiennent à une classe de systèmes de dimension infinie, appelées Représentations Diffusives. Dans Ref. [A2] ou [C4], en utilisant un processus mathématique limite, nous avons montré que R et T sont des fonctions de transfert associées à des tubes semi-infinis.

Pour la simulation numérique dans le domaine temporel, les représentations diffusives sont approximées par des systèmes de dimension finie (cf. eg. Ref. [A1]), puis la représentation d'état du résonateur est construite (cf. eg. Refs. [A4] ou [C6]). Les représentations d'état permettent d'utiliser les outils standards de l'automatique, cela afin de supprimer des boucles sans retards, de discrétiser le système et de réduire la complexité des calculs numériques, avec une méthode qui est modulaire.

Pour garantir la stabilité des simulations temporelles, la passivité et la stabilité du système ont été étudiées. En considérant le cas particulier des tubes évasés avec pertes visco-thermiques et continuité de section et de pente, la stabilité et la passivité ont été prouvées pour des courbures positives (0). En raison de la fonction (s), la démonstration n'est pas évidente, mais a pu être menée à terme en utilisant une extension du principe du maximum pour les fonctions holomorphes.

Le cas des tubes à courbure négative (0) est très délicat. La difficulté du problème vient d'un ensemble continu et infini (appelé coupure) de singularités instables dans le demi-plan droit du domaine de Laplace. Cependant, en utilisant le raisonnement de Ref. [A2] ou [C4], ce problème est maintenant bien connu et compris, et est similaire au problème de jonctions de cônes avec un saut négatif de pentes (cf. eg. [Välimäki95,Gilbert90]). Pour de tels systèmes, les fonctions de réflexions aux jonctions sont instables, mais le système global est naturellement stabilisé par la boucle avec retard qui modélise les aller-retours d'ondes dans le tube. Autant que nous savons, aucune preuve mathématique rigoureuse n'a été faite auparavant. Dans Ref. [C3], nous prouvons la stabilité des systèmes modélisant un cône convergent en utilisant la réalisation minimale du système, à la fois en temps-continu et en temps-discret.

Malheureusement pour les tubes à courbure négative cette méthode ne peut s'appliquer. Cependant pour leur simulation temporelle une autre méthode prometteuse a été obtenue : par factorisation algébrique, le système est mis sous une forme dite standard. Alors pour cette forme, nous montrons que parmi les 6 fonctions de transfert mises en jeu, 2 sont libres et peuvent être choisie arbitrairement. Les 4 autres sont alors données par des expressions qui permettent de laisser le système invariant du point de vue entrées/sorties. Ensuite, nous déterminons les 2 fonctions paramètres qui permettent d'une part de stabiliser la réalisation numérique du système, et d'autre part conservent le formalisme des guides d'ondes.

La figure 2 présente le résultat de la construction d'un trombone virtuel. Ce trombone virtuel est construit avec une embouchure modélisée, un tube constitué de 11 tronçons de tube (cylindriques, coniques et évasés pour le pavillon), et une impédance de rayonnement. Les paramètres du modèle ont été choisis en fonction de la mesure du profil géométrique faite sur le vrai trombone. L'impédance est calculée à partir du modèle approximé et simulable en temps-discret. Elle est comparée à la mesure d'impédance faite sur le vrai trombone.

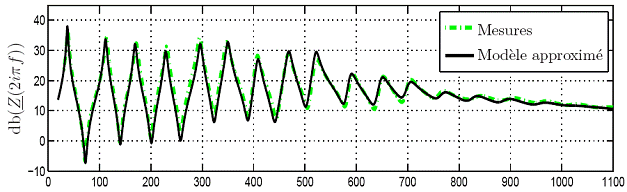
FIGURE 2 – Impédance d’entrée du trombone : Impédance mesurée sur un trombone réel, et impédance calculée par le modèle approximé.

Références :

[Smith87] J. O. Smith. Music applications of digital waveguides, Tech. Rep. STAN-M-39, Center for Computer Research in Music and acoustics (CCRMA), 1987.

[Matignon95] D. Matignon. Spectral and time-domain consequences of an integro-differential perturbation of the wave PDE, In WAVES'95, pp. 769-771, Mandelieu , France, 1995.

[Hélie03] T. Hélie. Unidimensional models of acoustic propagation in axisymmetric waveguides, J. Acoust. Soc. Am., vol. 114, pp. 2633-2647, 2003.

[Markel73] J. D. Markel and A. H. Gray. On autocorrelation equations as applied to speech analysis, IEEE Trans. Audio and Electroacoust., vol. 21, no. 2, pp. 69-79, 1973.

[Välimäki95] V. Välimäki. Discrete-time modeling of acoustic tubes using fractional delay filters, Ph.D. dissertation, Helsinski University of Technology, 1995.

[Gilbert90] J. Gilbert, J. Kergomard, and J.-D. Polack. On the reflection functions associated with discontinuities in conical bores, J. Acoust. Soc. Am., vol. 84, 1990.