La tâche traitée par l'équipe analyse-synthèse était de trouver une méthode par laquelle les dix-huit sons rassemblés par l'équipe psycho-acoustique pourraient être analysés, représentés et complètés. Ceci nécessitait donc d'utiliser un modèle permettant des manipulations faciles et la synthèse d'autres sons remplissant un espace perceptif incomplet.

Une difficulté supplémentaire tient à ce que les sons en question (étant mécaniquement dérivés) ne sont pas seulement harmoniques. Ceci signifie qu'il y a une importante composante de bruit dans les sons autant que de composante harmonique (ou tonale) provoquée par la répétition périodique des mécanismes des dispositifs de climatisation.

Ceci a impliqué que les sons ont du être analysés et représentés en utilisant deux méthodes. La première étape devait enlever et représenter le contenu harmonique (partiels) en termes de données sinusoidales, laissant de ce fait dans un fichier résiduel la composante de bruit. Ce fichier résiduel doit alors être représenté en utilisant un autre modèle facilement manipulable.

Une fois que les sons sont représentés de cette manière, la modification et la re-synthèse ou le mélange simple des divers composants peuvent être employés pour créer les sons qui manquaient dans l'espace psycho-acoustique .

Comme noté ci-dessus, les sons en question ont pu être décrits comme en partie harmoniques. C'est-à-dire, bien que les sons aitait une composante périodique bien définie, il y a aussi une autre composante qui est de nature plus aléatoire. La raison de ceci tient à la nature de la source sonore. Les mécanismes du dispositif de climatisation (moteur, ventilateur etc..) produisent un son à caractère très périodique. En outre, le flux d'air est susceptible d'avoir une fréquence de résonance qui fournira quelques éléments harmoniques. Cependant, la nature aléatoire du flux d'air et de tout autre phénomène acoustique moins prévisible ajoute une composante de bruit au son. Extraire seulement l'une ou l'autre de ces deux composantes ne permettrait évidemment pas la re-synthèse précise.

L'analyse initiale des fichiers de sons a démontré la présence dans tous les enregistrments d’une composante d’amplitude importante à la fréquence fondamentale d’environ 100Hz.

Cette valeur peut être attribuée à beaucoup de choses mais est très probablement reliée à une composante harmonique du courant secteur, d’une résonance d'appareils de contrôle ou encore de la salle. La conséquence utile de cela est qu'elle simplifie grandement la détection et la séparation de la composante harmonique.

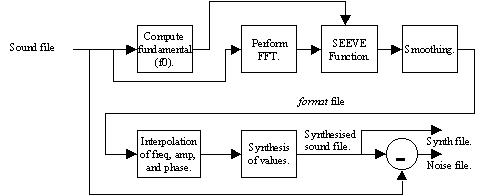
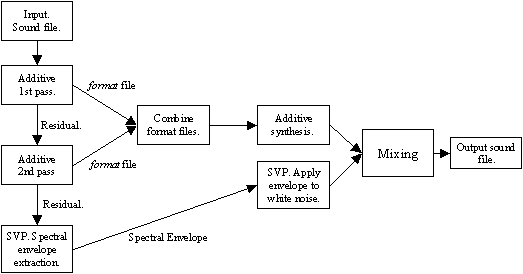
L'outil choisi pour extraire le contenu harmonique à partir du son est le programme " Additive " développé par l'équipe analyse-synthèse. Le fonctionnement d'Additive est d'analyser le fichier de son et d'identifier d'abord tous les partiels (pics reconnaissables dans le spectre d'amplitude) qui sont des harmoniques de la fréquence fondamentale du son. Il forme alors des trajets de partiels qui contiennent l'information sur la façon dont l'amplitude, la fréquence et la phase de chaque harmonique évolue dans le temps. La re-synthèse utilisant cette information est alors une simple question de synthèse additive des partiels. Un diagramme simplifié du processus entier peut être vu ci-dessous dans figure 1.

Premièrement, la fréquence fondamentale du son est estimée en des instants régulièrement espacés sur toute la durée du fichier. Additive exécute alors une FFT qui fournit un spectre en chacun de ces instants. Les pics dans le spectre sont alors identifiés et seuls sont gardé ceux qui sont des harmoniques de la fréquence fondamentale estimées. Cette dernière partie est effectuée dans la fonction de Seeve. Après ceci, les naissances et les décès eventuels des partiels sont lissés et un fichier est produit (appelé fichier format) qui contient l'information (fréquence, amplitude et phase) sur chaque partiel dans le son à chacun des instants d'analyse (les trames). La re-synthèse consiste en une interpolation, pour chaque paramètre, entre deux valeurs successives dans les trames adjacentes et une synthèse additive simple.

Le fichier de son qui est laissé après l'extraction de la composante harmonique contient la composante aléatoire de 'bruit' du son. Il y a plusieurs voies pour représenter ce type de son mais la plus connue, et celle qui présente le plus de possibilités de manipulation des données, est l'utilisation des enveloppes spectrales.

L'enveloppe spectrale du bruit est, dans ce cas, simplement l'enveloppe du spectre d'amplitude du signal résiduel. Cette enveloppe peut être extraite en utilisant un outil développé à l'Ircam et appelé Super VP (Super Vocoder de Phase). Super VP peut fournir un fichier contenant l'amplitude du spectre à chaque valeur de fréquence. La résolution peut être ajustée en utilisant des FFTs de différentes tailles.

Une fois que cette enveloppe est extraite et enregistrée, elle peut alors être appliquée à un fichier de bruit blanc pour recréer le bruit initial. Ceci fonctionne parce que le fichier résiduel de Additive doit contenir seulement le 'bruit' et ainsi peut être synthétisé par la modification du spectre de fréquence d'un bruit blanc. De fait, dans une seconde passe de Super VP, l'amplitude du bruit blanc à chaque fréquence est multipliée par la valeur de l'amplitude de l'enveloppe spectrale du fichier initial de bruit. Enfin, quand les fichiers synthétisés d'harmoniques et de bruit sont mixés, alors le taux du mélange peut être ajusté à volonté.

Les expériences initiales avec Additive ont été prometteuses et indiquaient que le contenu harmonique dans le son constitue une grande partie de l'information globale. Cependant, le son de re-synthèse a un léger aspect métallique qui le fait sembler trop synthétique pour les buts de l'équipe psych-oacoustique. Il y avait deux raisons à ceci; Premièrement, le contenu harmonique était essentiellement présent dans les fréquences les plus basses (jusqu' à environ 8KHz) et ainsi le contenu au-dessus de cette fréquence n'était pas vraiment harmonique. La limitation du nombre de partiels à soixante-dix a facilement résolu ce problème. Avec une fréquence fondamentale de 100Hz ceci a alors fourni des informations sur le contenu harmonique jusqu' à 7KHz. La deuxième raison de la qualité synthétique du son provient de l'estimation de la fréquence fondamentale. Bien que la fréquence fondamentale ait été certainement identifiable à environ 100Hz (+/- 8Hz) il y avait des variations dans le fichier de la fréquence fondamentale qui sautait parfois momentanément à une fréquence radicalement différente, ceci étant clairement une mauvaise estimation plutôt qu'un changement réel de la fréquence fondamentale. L'effet était que les partiels dans le fichier format (étant dérivés de la fréquence fondamentale ) sautaient également parfois à une fréquence différente. Cette instabilité dans la fréquence fondamentale avait comme conséquence une tonalité peu réaliste du signal re-synthétisé.

La méthode pour corriger ceci était simplement de fixer la fréquence fondamentale à une valeur stable pour la durée du son. Comme indiqué préalablement, les fréquences fondamentales de tous les fichiers considérés étaient autour de 100Hz. Un programme a été écrit permettant d’assigner toutes les valeurs d’un fichier de fréquence fondamentale à une valeur fixe. (fréquence a chaque instant d'analyse). Dans notre cas, la valeur de 100Hz a été utilisée. Le résultat est un son de re-synthèse bien plus naturel.

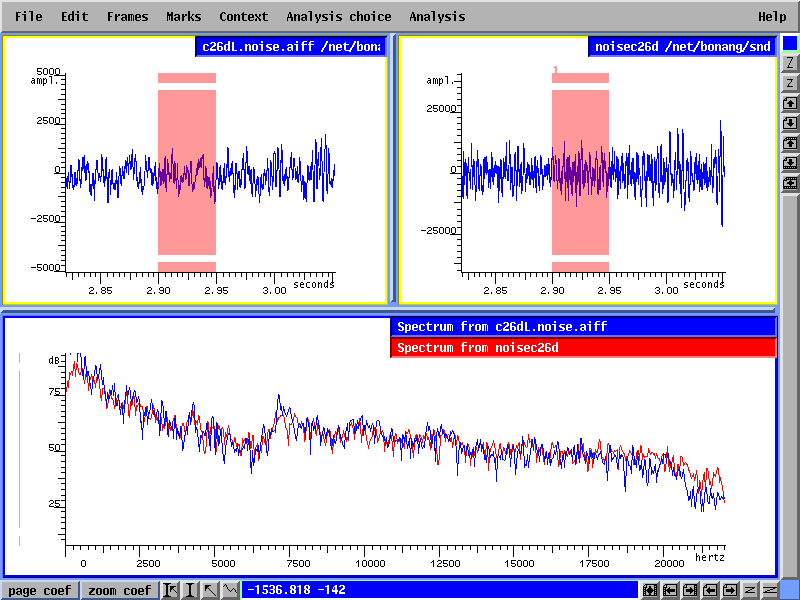
L'expérimentation avec Super VP a fourni une méthode pour extraire l'enveloppe spectrale et pour la représenter sous une forme facile à modifier si nécessaire. Le fichier résultant contient l'enveloppe du fichier de bruit en différents instants pour toute la durée d'un son. Les données ont été simplement enregistrées comme des valeurs normalisées en virgule flottante et sont ainsi très faciles à afficher graphiquement et, de même, à manipuler. La figure 2 ci-dessous montre une enveloppe spectrale du fichier de bruit pour un des sons étudiés en fonction de la fréquence:

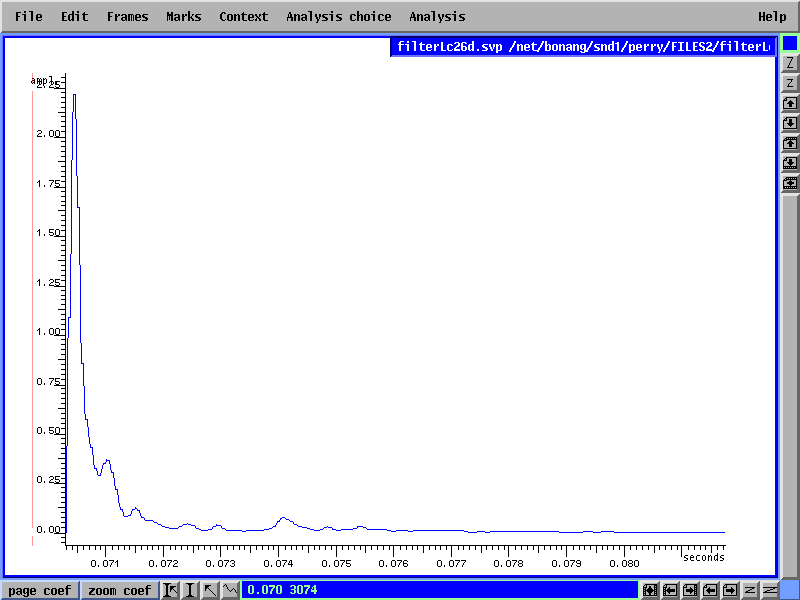
Les valeurs de ce fichier sont employées pour multiplier les valeurs d'amplitude de la transformée de Fourier d'un fichier de bruit blanc. Le résultat est alors synthétisé pour créer un nouveau fichier de bruit ayant l'enveloppe spectrale voulue ainsi obtenue. Ceci a bien fonctionné sauf que l'amplitude globale du bruit n'est pas toujours préservée. Après la discussion avec l'équipe de psychoacoustique, la décision a été faite de ne pas résoudre ce problème automatiquement et de simplement régler le mixage des fichiers synthétisés d'harmoniques et de bruit manuellement. En effet, l'objectif final étant de produire de nouveaux fichiers de sons, il semble raisonnable qu'un certain degré de manipulation manuelle des paramètres soit nécessaire de toute façon.

A ce point, ayant une méthode pour l'analyse et la synthèse des deux composantes des fichiers de sons, un programme a été écrit pour exécuter automatiquement l'analyse et la re-synthèse. Ce programme a été alors testé sur une partie des fichiers à étudier.

Des résultats encourageants et des re-synthèses assez précises de la plupart des sons ont pu être réalisés. Cependant, il est apparu qu'une information de basse fréquence manquait dans la plupart des sons synthétisés. L'examen de l'éventail des fréquences des originaux et des signaux synthétisés l'a confirmé. La figure 3 ci-dessous montre les résultats d'une analyse spectrale des deux fichiers:

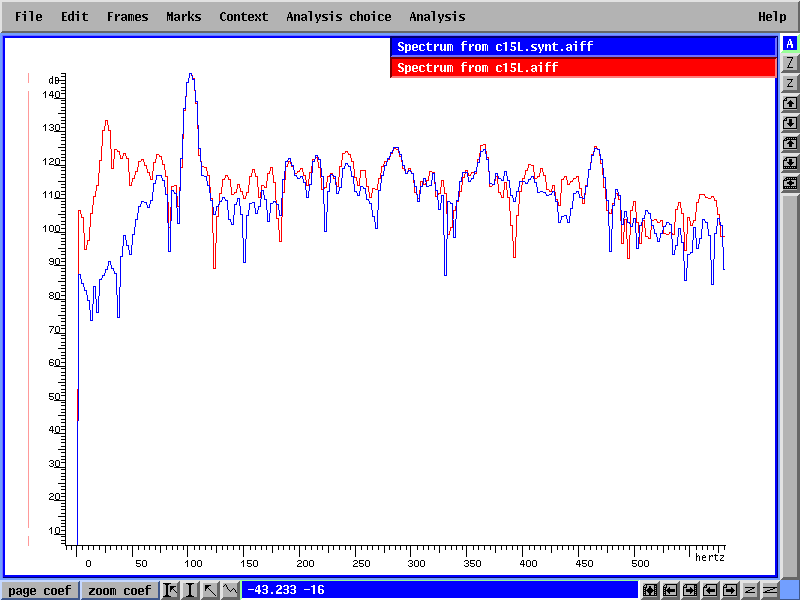
On peut facilement voir que le fichier synthétisé a moins de basses fréquences. Ceci a suggéré qu'il y ait encore de l'information harmonique qui n'avait pas été extraite par Additive. Comme expliqué plus tôt, tout contenu harmonique resté dans le résiduel ne sera pas synthétisé par la méthode d'enveloppe spectrale et sera donc ainsi perdu.

Le problème est apparu être la présence d'une seconde fréquence fondamentale à environ 30Hz. Avec le positionnement de la première fréquence fondamentale à 100Hz, toute l'information au-dessous de cette fréquence était ignorée. Cependant, placer la fréquence fondamentale à 30Hz pour l'analyse entière prendrait trop de partiels alors que les harmoniques de 30Hz semblent s'étendre seulement jusqu'autour de 200Hz. Traiter le fichier entier avec cette fréquence fondamentale extrairait un grand nombre de composantes harmoniques erronés.

La solution était d'utiliser deux passes d'Additive La première passe a utilisé la même fréquence fondamentale de 100Hz que précédemment et une deuxième passe a été exécutée sur le fichier résiduel de la première passe en utilisant la fréquence fondamentale de 30Hz. Cette deuxième passe a été employée pour extraire toute l'information au-dessous de 100Hz, avant d'employer finalement Super VP pour extraire l'information de bruit. La deuxième passe a été également exécutée avec un nombre de partiels limité à six pour s'assurer que seulement l'information ommise par la première passe serait considérée.

Un nouveau programme alors a dû être écrit pour combiner les sorties des deux passages de Additive. Celles-ci étaient sous forme de deux fichiers format (voir figure 7). Une fois ces deux fichie’s combinés, le fichier simple résultant peut être passé vers l'étape de synthèse de Additive et la sortie est alors un fichier de son avec une meilleure représentation de la teneur de l'original en basses fréquences. La figure 4 ci-dessous montre le spectre d'amplitude du son synthétisé comparé à l'original en utilisant la nouvelle méthode de deux passages.

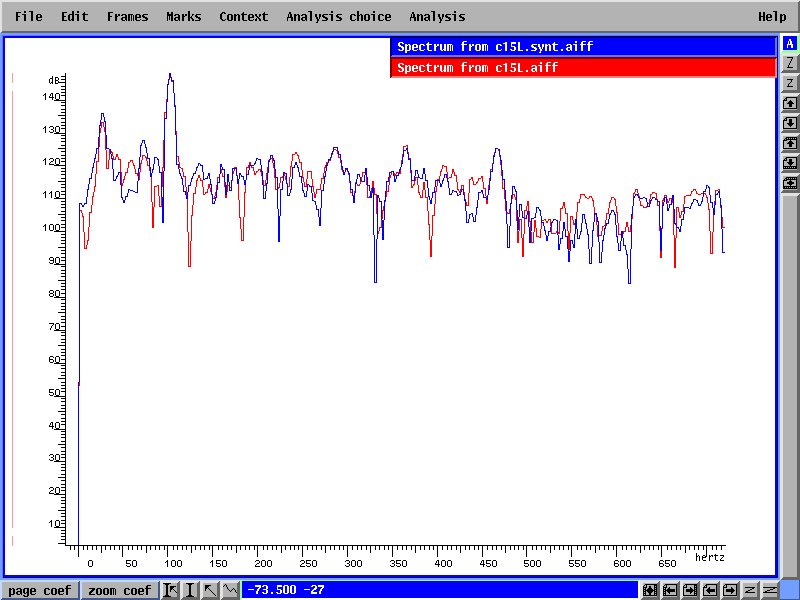
On peut voir maintenant que l'information de basse fréquence a été extraite et synthétisée et que la méthode de base pour l'analyse totale des sons en question est complète.

Un organigramme du processus entier d'analyse/re-synthesis peut être vu dans la figure 5 ci-dessous:

Le processus est en grande partie automatique, la seule partie exigeant une intervention est le rapport de bruit et de fichier de son harmonique à l'étape de mixage.

La figure 6 ci-dessous montre les fichiers et les spectres synthétisés d'harmoniques et de bruit, comparés au fichier initial et au fichier résiduel respectivement.

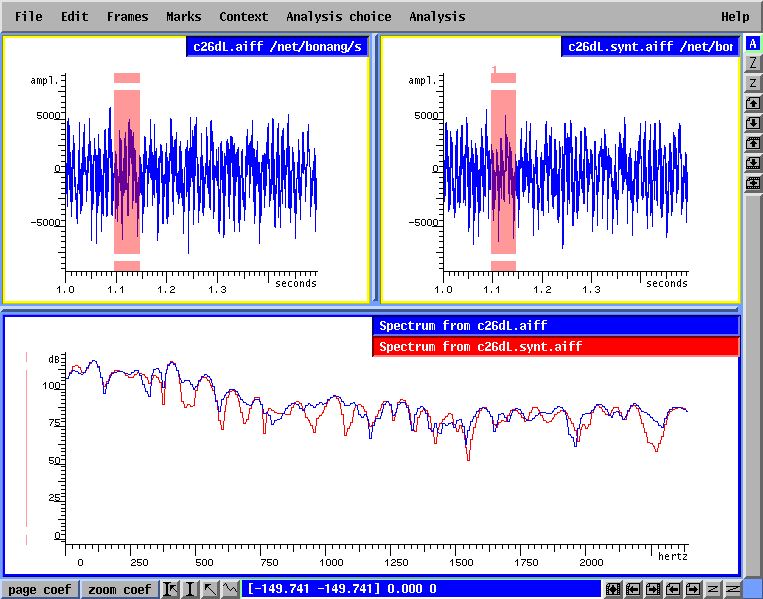
Ces deux spectres montrent la bonne similitude entre l'original et chaque composant synthétisé.

Une fois que la méthode décrite ci-dessus a été établie, la prochaine tâche était de trouver une méthode pour l'interpolation entre les sons. Il était requis que la méthode fournisse la possibilité d'interpoler linéairement entre deux sons quelconques et qu'il soit possible de choisir le coefficient d'interpolation entre un et zéro.

La méthode pour l'interpolation pour chacun des deux types de données (des fichiers d'harmoniques et des fichiers d'enveloppes spectrales) devrait être différente pour les deux types de données différents.

Un exemple du fichier format produit par l'étape d'analyse Additive peut être vu dans figure 7 ci-dessous:

L’interpolation des données consiste en l'interpolation de l’amplitudes et de la fréquence de chacun des partiels avec son équivalent dans l'autre fichier. Si aucun partiel équivalent n'existe dans l'autre fichier (des harmoniques manquant dans un fichier par exemple) alors la fréquence du partiel existant est utilisée et l'amplitude interpolée avec la valeur zéro. Les partiels dans chaque fichier sont identifiés par la valeur de l'index qui esl le numéro de l'harmonique de la fréquence fondamentale que le partiel représente. L'interpolation entre les fichiers utilise cet incrément comme guide pour les partiels à interpoler entre dans chaque trame de chaque fichier. Un petit programme a été écrit pour accomplir cette tâche.

Partiels 1. Partiels 2.

Fichier format interpolé.

Par cette méthode les paramètres d'amplitude et de fréquence de n'importe quel fichier format ont pu être interpolés avec des autres. De plus, le coefficient pour l'amplitude et la fréquence peuvent avoir des valeurs différentes. Ceci fournit un outil très précis d'interpolation pour le contenu harmonique des fichiers initiaux.

L'une des raisons pour lesquelles les enveloppes spectrales ont été choisies comme méthode pour représenter la composante de bruit des sons est qu'il est relativement facile de les interpoler. Chaque trame du fichier spectral d'enveloppe contient des valeurs des composantes d'une enveloppe spectrale d'amplitude pour un nombre donné de valeurs de fréquence. Ainsi, pour interpoler entre les enveloppes, il suffit d'interpoler entre les amplitudes de valeurs équivalents dans les trames équivalentes de chaque fichier. Un petit programme a été écrit pour accomplir cette tâche.

La figure 8 ci-dessous montre, en gris, deux enveloppes spectrales et, en noir, l'enveloppe interpolée entre elles:

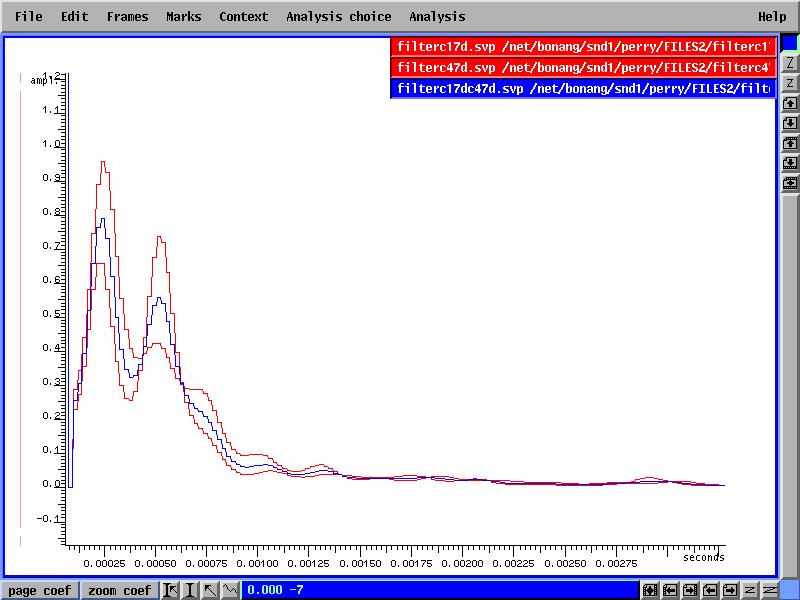
On voit facilement que le procédé d'interpolation a produit une enveloppe qui s'adapte parfaitement entre les deux autres. Comme avec l'interpolation des données harmoniques, le coefficient d'interpolation peut être ajusté entre zéro et un.

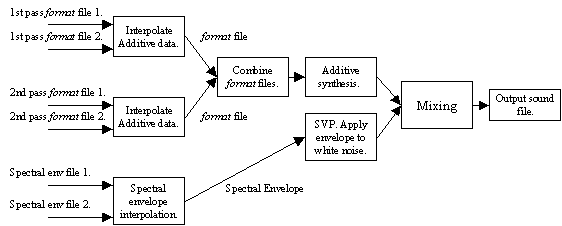
Le processus complet permet l'interpolation indépendante de l'amplitude et de la fréquence des partiels dans les données harmoniques, et entre les enveloppes spectrales. De plus, le taux d'harmoniques et de bruit peut être modifié pour ajuster objectivement le son interpolé final. Un organigramme du procédé complet d'interpolation peut être vu dans figure 9 ci-dessous:

La tâche pour laquelle la méthode a été développée était d'interpoler, avec des coefficients donnés, entre des sons dans un espace perceptuel psycho-acoustique. L'espace en question est tridimensionnel et contient 18 sons. Le but était de placer de nouveaux sons dans l'espace pour créer une distribution plus uniforme.

Les sons avaient été placés dans l'espace en utilisant des tests de similaritè qui avaient fourni une solution en deux et en trois dimensions. Les sons occupent simplement la place correspondant à leurs coordonnées sur les axes. La solution bidimensionnelle a également fourni une valeur pour la spécificité de chaque son. Cette valeur définit à quel point chaque son pourrait être considéré comme unique par rapport aux autres. Bien que nous n'ayons pas utilisé le modèle bidimensionnel, cette valeur s'est avérée être utile plus tard.

Cinq interpolations ont été définies par l'équipe psychoacoustique pour créer une meilleure répartition des sons dans l'espace. Des coefficients d'interpolation de 0,5 environ ont été fixés pour tous les paramètres. Cependant, bien que l'interpolation ait bien fonctionné, les sons résultants pour deux des interpolations n'ont pas semblé convainquants. Ces deux sons ont été produits par une interpolation avec un son particulier, le son c34. Sa valeur de spécificité s'est révélée la plus élevée de beaucoup et ceci a suggéré que les sons avec des spécificités élevées sont difficile à interpoler. En conséquence, l'équipe de psychoacoustique a conçu un nouvel ensemble d'interpolations.

Le nouvel ensemble d'interpolations est plus petit (quatre au lieu de cinq) et évite les sons avec des spécificités élevées. Il a également nécessité l'utilisation de coefficients d'interpolation plus précis.

Les interpolations et coefficients sont:

1. c40 --- c29, a = 0.53.
2. c17 --- c27, a = 0.33.
3. c26 --- c42, a = 0.2.
4. c11 --- c42, a = 0.7.

Dans deux cas, les coefficients indiqués ont donné des résultats très bons et ont exigé un réglage seulement à l'étape de mixage. Ce mixage objectif est nécessaire simplement pour assurer un équilibre correct entre l'harmonique et le contenu de bruit. Il pourrait être possible d'automatiser ce processus mais c'est l'opinion des auteurs que ceci ne fournirait pas toujours les meilleurs résultats. La réalisation d'un équilibre réaliste entre les harmoniques et le bruit est très individuelle à chaque son et se fonde sur le caractère de chacun. Ce taux peut ne pas être identique non plus à celui des fichiers à partir desquels le fichier interpolé a été créé.

Dans les deux cas cependant, les valeurs imposées pour le coefficient n'ont pas fourni de sons réalistes. Dans ces cas il a été nécessaire de modifier les coefficients légèrement pour chacun des types d'interpolation (amplitude, fréquence, enveloppe spectrale) pour réaliser un son avec un timbre naturel. La difficulté avec l'interpolation est qu'une interpolation mathématiquement parfaite peut ne pas fournir un son qui soit naturel à l'oreille. Ainsi, il était important d'avoir le contrôle manuel de différents paramètres.

Les valeurs qui ont été utilisées pour les coefficients dans l'interpolation sont montrées ci-dessous.

a = coefficient pour l'amplitude des partiels dans les données harmoniques

b = coefficient pour la fréquence des partiels dans les données harmoniques

s = coefficient pour l'amplitude de l'enveloppe spectrale.

1. c40 --- c29, a = 0.43, b = 0.63, s = 0.53.
2. c17 --- c27, a = 0.33, b = 0.33, s = 0.33.
3. c26 --- c42, a = 0.2, b = 0.2 , s = 0.2.
4. c11 --- c42, a = 0.8, b = 0.6 , s = 0.7.

Avec ces valeurs, des sons réalistes ont été obtenus et fournis à l'équipe psychoacoustique pour l'étape suivante de test.