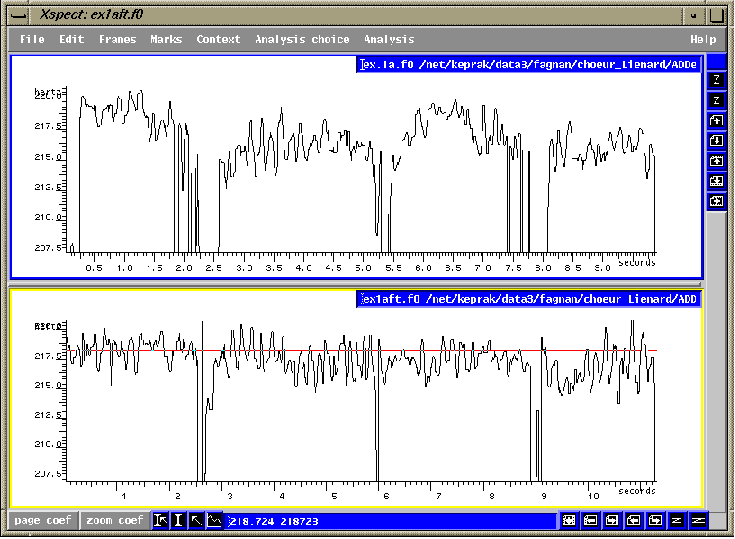
fig. 1.1 Un choeur chantant [i], [a], [i], [a] au la 3 (220Hz). Notez que la fréquence fondamentale est beaucoup plus stable et consistante dans la deuxième fenêtre.
Depuis plusieurs années
je témoigne de l'effet positif que peuvent avoir les principes vocaux
de la méthode bel canto sur le chant choral. Ces principes
sont depuis très longtemps acceptés dans le domaine du chant
solo, mais c'est d'habitude avec beaucoup de crainte que les chefs de choeur
pensent à appliquer ces principes à la technique vocale d'un
choeur. Cependant, cette étude que nous entreprenons à
l'Ircam (Institut de recherche et coordination acoustique/musique) éclairci
ce point et offre des possibilités d'application efficace des principes
bel canto au chant choral. Les analyses inclues dessous offrent
des quantifications acoustiques objectives de l'application de cette méthode.
Toutes les expériences ont
eu lieu dans l'Espace de Projection à l'Ircam à Paris.
Dans un premier temps le chef de choeur de l'ensemble a fait chanter douze
exercices par son choeur. Ensuite, un travail a été fait
pendant 90 minutes sur plusieurs principes centraux de la méthode
bel canto. Les mêmes exercices ont été enregistrés
à nouveau pendant ce travail. Finalement, la comparaison de ces
deux versions des mêmes exercices a mené aux analyses ci-dessous.
Dans ces analyses, la première fenêtre représente un
exercice chanté par un choeur avant d'avoir travaillé le principe
en question, et la deuxième le même exercice après d'avoir
travaillé le principe bel canto.
Les outils d'analyses qui ont
été développés a l'Ircam, ainsi que l'assistance
de Xavier Rodet, ont été fort utiles dans ma démarche
de pouvoir montrer de façon objective et scientifique les avantages
acoustiques de cette méthode.
Considérons premièrement
comment le coup de glotte proposé par Manuel Garcia peut avoir
un effet positif sur la régularité de la vibration et de la
fréquence fondamentale (fig.1.1). Avec ce principe, les choristes
sont encouragés à légèrement fermer la glotte
avant l'attaque qui part de la position fermée afin d'assurer une
vibration plus contrôlée et régulière.

fig. 1.1 Un choeur chantant [i], [a], [i], [a] au
la 3 (220Hz). Notez que la fréquence fondamentale est beaucoup plus
stable et consistante dans la deuxième fenêtre.
La vibration régulière a aussi ses effets sur l'énergie spectrale d'un choeur (fig 1.2):
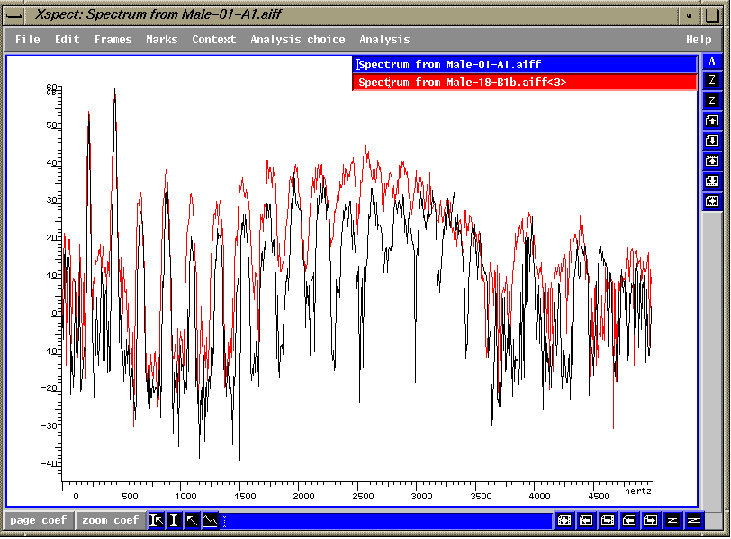
fig. 1.2 Choeur d'hommes qui chante un [i]. Le spectre
en rouge représente l'analyse avec l'application de la vibration
bel canto
Notons que les deux premiers
partiels dans cet exemple sont de la même intensité. Par contre
à partir de ce point, et surtout près des formants, il existe
une augmentation remarquable dans l'énergie spectrale de la version
plus vibrante. C'est dans la région du formant des chanteurs (2.3-3.5kHz),
là ou l'oreille est la plus sensible, que l'écart entre les
deux exemples est le plus remarquable. Ceci montre bien l'efficacité
acoustique supérieure que la vibration donne à la voix.
Avec le sonagramme, nous avons une autre façon de montrer cette différence (fig.1.3).
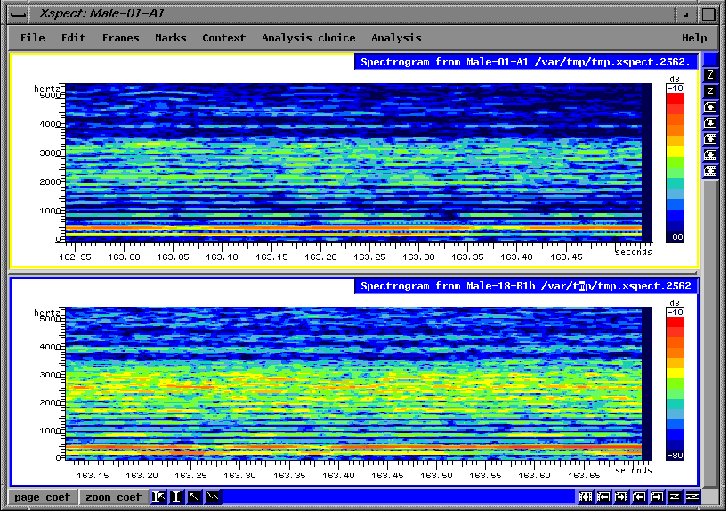
fig.1.3 Même extrait
sonore que fig.1.2 avec sonagramme.
Il est clair qu'il y a plus d'intensité dans la région de la fondamentale dans le premier exemple (orange foncé) mais beaucoup plus d'énergie dans les hautes fréquences dans le deuxième.
***EXEMPLE SONORE
avant*** (choeur d'hommes adolescent qui chante [i] au "la 3")
***EXEMPLE SONORE
après***
Si nous extrayons l'énergie dans la bande de fréquences entre 2.3 et 3.5kHz (fig.1.4), nous voyons très clairement la supériorité spectrale de la version plus vibrante. Grâce à cette analyse nous pouvons constater qu'il y a 22dB de plus d'énergie dans cette région spectrale après que le principe de la vibration régulière a été appliqué. Lorsque nous considérons que les premiers partiels étaient au même niveau, il devient évident que cette deuxième tentative est acoustiquement beaucoup plus efficace. N.B. L'axe "y" ne devrait pas lire "hertz" mais plutôt "dB" (intensité) .
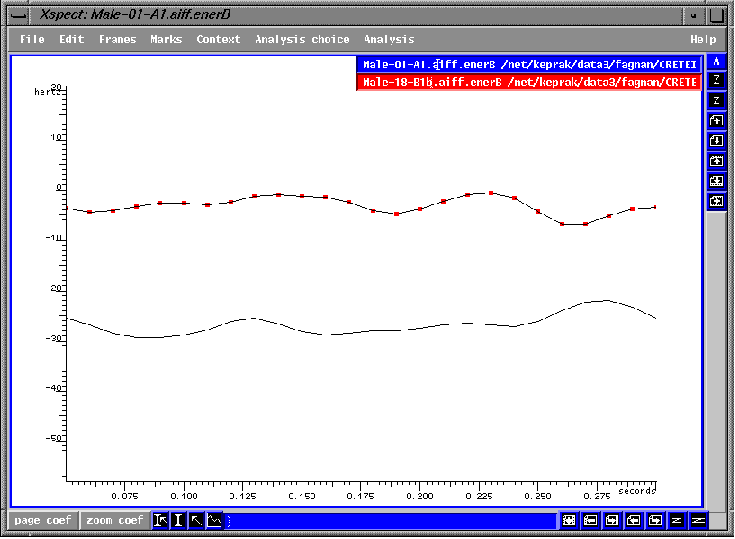
fig.1.4 Mesure de l'énergie spectrale dans la
bande spectrale de 2.3 a 3.5kHz (formant des chanteurs).
Cette façon de mesurer l'énergie spectrale dans cette bande de fréquences a été extrêmement importante et utile à cette étude. Elle nous a permis de mesurer objectivement cette énergie et me permettra de réfuter beaucoup de ce qui a été écrit sur la technique vocale des choeurs et, en particulier, sur le manque d'énergie dans cette bande.
Les chefs de choeur craignent
souvent la présence d'une vibration régulière (à
ne pas confondre avec le vibrato qui peut devenir un effet secondaire de
cette vibration régulière) et préfèrent un son
qui a moins d'intensité, croyant que ceci est plus propice à
un bon ensemble vocal. Cependant, il est évident que la vibration
idéale enseignée par les grands maîtres du bel canto
mène à un son beaucoup plus complet ainsi qu'une émission
plus efficace.
Il est très bien connu
que toutes les voyelles ne résonnent pas de la même façon
ni à la même fréquence. Pour changer de voyelle le conduit
vocal doit changer de forme. Ce mouvement peut porter une altération
importante à la façon de laquelle la résonance peut
influencer la justesse en chant. Ce phénomène a souvent
été observé par des acousticiens de la voix sous les
rubriques de "the intrinsic pitch of vowels" et "articulatory F0 perturbations."
Par exemple, plusieurs expériences ont montré que le changement
de "i" a "E" (elle), est souvent accompagné d'une baisse
assez importante de la fondamentale. Le lien entre changement de résonance
et changement de vibration des cordes vocales (fréquence) semble être
très fort.
Cependant, nous avons trouvé
que cette influence péjorative peut être réduite, voir
supprimée, lorsque le principe de résonance bel canto
de chiaroscuro est observé. Quoique certaines voyelles
soient plus chiaro ou oscuro que d'autres par nature, ce principe
cherche à établir une proportion égale de brillance
et de richesse dans toute la gamme des voyelles chantées. Cette consistance
sert à égaliser les partiels supérieurs dans les voyelles,
un phénomène qui, comme le témoignent les analyses qui
suivent, aide à renverser l'effet péjoratif de la hauteur intrinsèque
des voyelles.
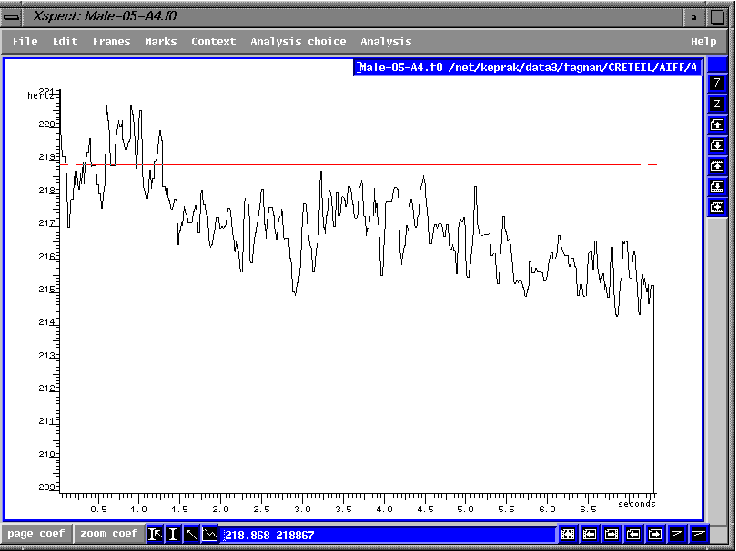
fig.2.1 Choeur qui chante les voyelles [i]-[E (
elle)]-[y (tu)]-[a] avant le travail de chiaroscuro
.
***EXEMPLE SONORE
avant*** (fig.2.1)
***EXEMPLE SONORE
après*** (fig.2.2)
La ligne rouge des fig. 2.1
et 2.2 est placée à la fréquence moyenne de la première
voyelle chantée [i] tel que calculée par le programme Additive
de l'Ircam. Nous pouvons facilement noter une baisse importante de presque
2Hz lorsque la mâchoire inférieure s'ouvre en passant de [i]
à la deuxième voyelle de [E] (à 1.5 sec.). La fréquence
fondamentale monte encore lorsque la mâchoire se referme légèrement
pour le [y] (2.2 sec), et baisse encore pour la dernière voyelle de
[a] (5.5 sec). Ces ondulations de la fréquence fondamentale
selon la voyelle chantée correspondent parfaitement aux résultats
des expériences effectuées par Sten Ternstrom et Johan Sundberg
à Stockholm.1 Ce phénomène
fait d'ailleurs le sujet de leurs articles "Intonation Precision of Choir
Singers," et "Articulatory f0 Perturbations and Auditory Feedback."
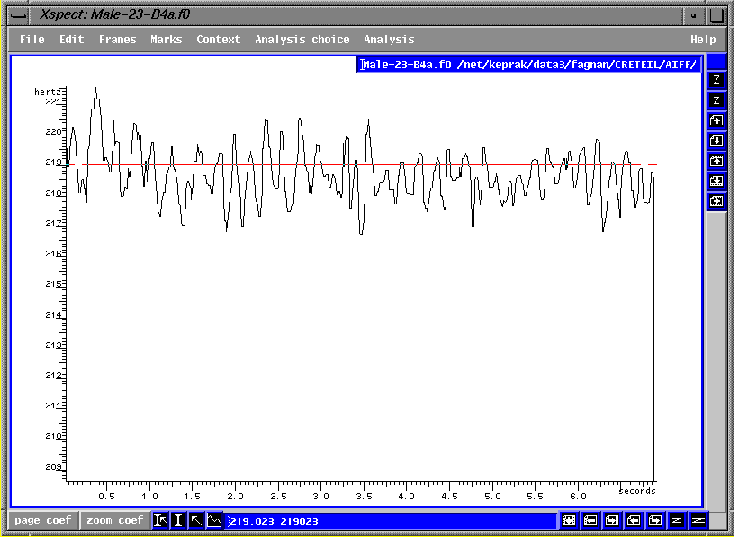
fig.2.2 Choeur qui chante les voyelles [i]-[E (
elle)]-[y (tu)]-[a] en appliquant la technique de résonance
chiaroscuro
A comparer avec la fig.2.1.
Nous pouvons constater d'après la figure 2.2 que ce phénomène a été renversé après un travail d'environ quinze minutes sur l'équilibre des résonances par le principe de chiaroscuro. La baisse de la première voyelle à la dernière était de 3.22Hz dans la figure 2.1 tandis qu'elle est maintenant de 0.29Hz.
Les exemples "avant" et "après" qui suivent témoignent du
même effet positif.
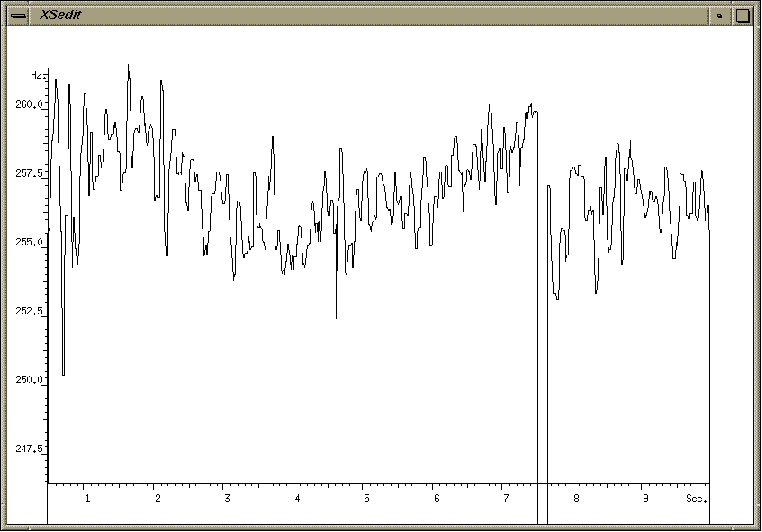
fig.2.3 Choeur d'hommes chantant la phrase
kyrie e leison avant chiaroscuro, au do moyen.
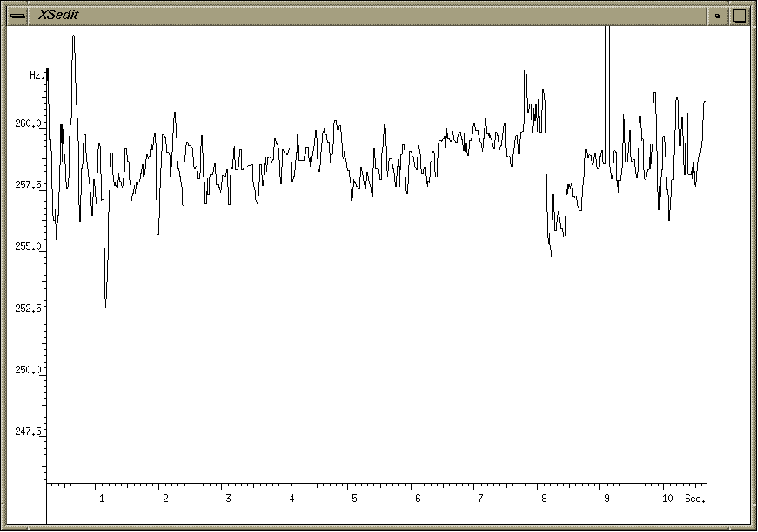
fig.2.4 Kyrie e leison après avoir travaillé
le chiaroscuro (même choeur que fig. 2.3).
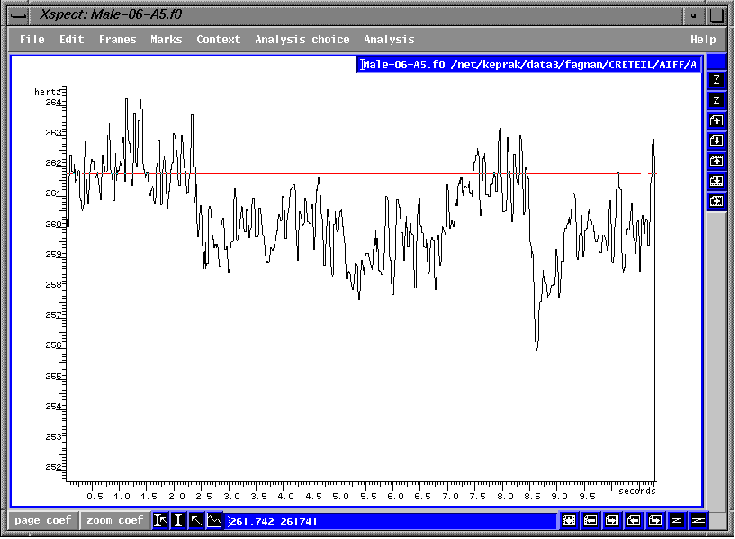
fig.2.5 Kyrie et leison avant
(choeur d'hommes adolescent).
Nous devons cependant noter qu'avec l'application du principe de chiaroscuro, il y a parfois une tendance de surcompenser pour la tendance naturelle de baisser pour les voyelles plus sombres. Dans la figure 2.6, le choeur a bien compensé pour les voyelles plus obscures en leur ajoutant plus de brillance, et on ne remarque aucune baisse entre le premier [i] et les trois [E] qui suivent (de 0 à 6.5 sec.). Cependant, lorsque les choristes regagnent le [i] de leison (7 à 8.5 sec.), ils la chantent trop haute, étant toujours dans l'esprit de compensation résonatoire. Cependant, on remarque que cette même hausse était présente dans le premier exemple (fig.2.5). Mais c'est un point à souligner et à corriger.
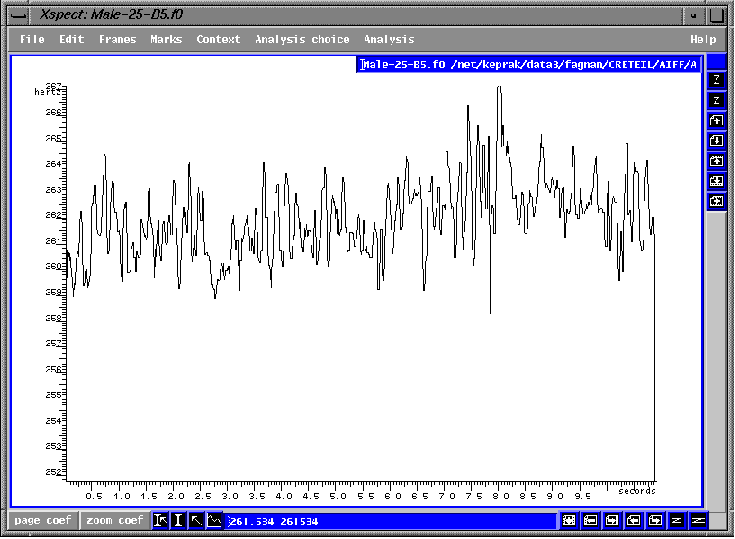
fig.2.6 Kyrie e leison après
(même choeur que fig. 2.5).
Cependant, dans la majorité des cas, le principe de chiaroscuro semble fournir aux choristes un outil de justesse fort efficace tel qu'indiqué dans les prochains exemples.
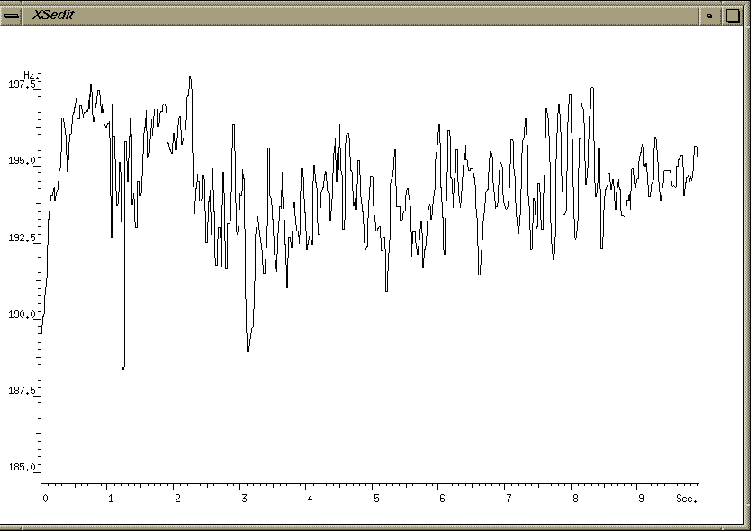
fig.2.7 Choeur d'adulte mixte (notes des hommes seulement)
chantant la phrase Christus factus est pro nobis-avant.
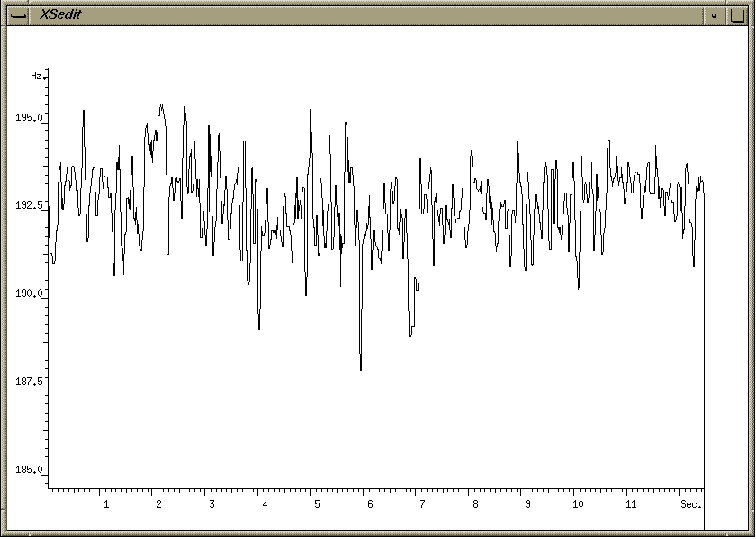
fig.2.8 Même choeur après avoir travaillé
le chiaroscuro.
Dans cet exercice le
plus grand changement dans la fréquence fondamentale du premier exemple
(fig.2.7) était la baisse de presque 4Hz entre le [i] (0.1-1.1 sec.)
et le [a] (2.2-4 sec.). L'ensemble a aussi baissé de 2Hz depuis
le début de l'exercice à la fin. Par contre, après
avoir travaillé le chiaroscuro, la baisse entre le [i] et le
[a] a été réduite a 1Hz et la fréquence fondamentale
est exactement la même à la fin qu'au début de l'exercice,
soit 193.11Hz. Il faut souligner que ce phénomène, où
l'exercice se termine exactement à la même fréquence
que celle où il a débuté, a été observé
dans 2 cas sur 5 avec l'application du chiaroscuro.
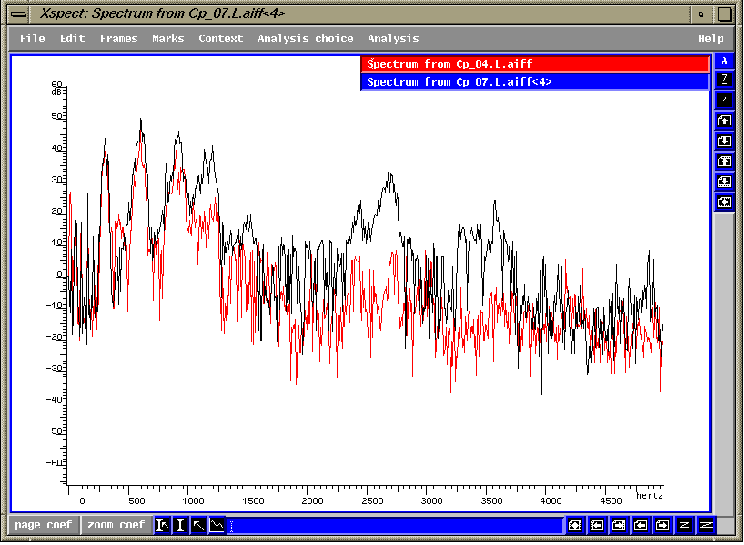
fig.3.1 Choeur d'hommes qui
chante un Mib4, premier 0.4 secondes de l'attaque. Le spectre de la version
bel canto est en noir; avant est en rouge.
fig.3.2 Même exemple qu'à la figure 3.1
montré avec le temps dans un sonagramme.
Cette prochaine analyse (fig.3.3)
par le programme enerBande montre l'évolution d'énergie dans
la région du singer's formant dans les premières 0.4 secondes
du même exercice, soit -66dB avant et -18dB après
(une amélioration de 48dB). Encore une fois, l'axe "y" est en dB et
non en hertz.
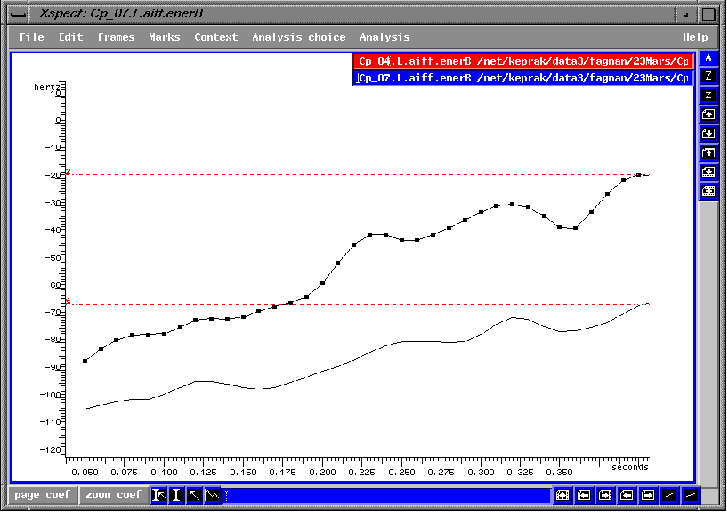
fig.3.3 Mesure l'évolution de l'énergie
dans la bande de 2.3 a 3.5kHz dans les premières 0.4 secondes; correspond
aux figures 3.1 et 3.2. Avant: De -104dB a -66dB.
Après: De -87dB a -18dB. Donc les hautes fréquences apparaissent
beaucoup plus tôt avec l'application de la nota mentale.
***EXEMPLE SONORE
(avant)***
***EXEMPLE SONORE
(après)***
Notons la quantité d'air
présente dans la première version ainsi que la voyelle mal
préparée et la faiblesse d'intensité. Ces éléments
péjoratifs ont été remplacés par une énergie
de vibration et de résonance complète au tout début de
la phrase après le travail de la nota mentale. Nous pouvons
entendre une voix qui ressort de l'ensemble (après); un fait à
noter et à travailler
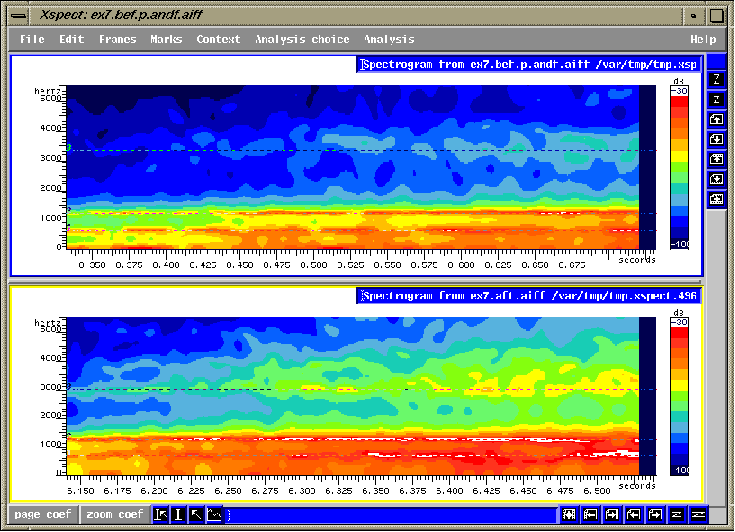
fig.3.4 Choeur mixte universitaire chantant le début
d'un accord à quatre son (alléluia).
Dans la figure 3.4 nous voyons
que tous les formants (lignes foncées horizontales) sont présents
au début de l'attaque dans la deuxième version. Celle-ci aura,
par conséquent, une voyelle beaucoup plus perceptible et juste au
début de la phrase. Nous remarquons aussi une forte augmentation d'énergie
dans la région de 3kHz. Ceci est grâce à une résonance
et une vibration qui ont été imaginées et préparées
sur l'inspiration, comme le conseillaient les maîtres du bel canto
.
Ce principe assure une consistance
d'énergie vocale et de justesse lorsqu'un choeur chante doucement
ou effectue un decrescendo a l'intérieur d'une phrase musicale.
Depuis longtemps nous savons que la plupart des choeurs perdent énormément
d'énergie de résonance et de vibration lorsqu'ils chantent
doucement, et ont donc du mal à se faire entendre et comprendre.
Par l'entremise du principe de messa di voce, la pédagogie
bel canto conseille de changer de nuances tout en maintenant 100%
d'énergie de vibration et de résonance chiaroscuro dans
la voix. Le contrôle du souffle doit aussi augmenter car l'air a naturellement
tendance à monter et dissiper la vibration lorsqu'on chante plus doucement.
Encore une fois, le programme Enerbande
nous a permis de calculer rapidement et d'afficher de façon claire
la consistance (ou manque de consistance) d'énergie présente
dans un decrescendo. Dans la figure 4.1, nous pouvons très bien voir
l'écart qui se développe entre le premier decrescendo (gris)
et le decrescendo qui applique le principe de messa di voce (noir).
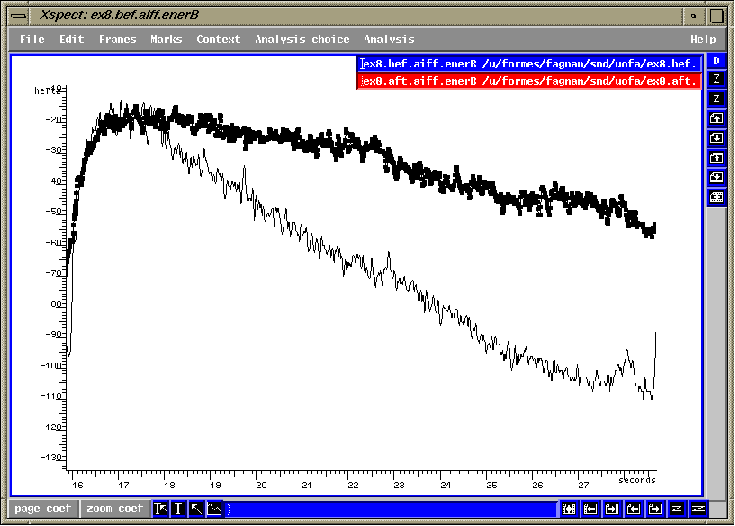
fig.4.1 Un decrescendo de forte à
pp effectué par un choeur mixte. Gris: avant, Noir: après.
Les analyses qui suivent sont extraits de la figure 4.1 et mesurent aussi l'énergie uniquement dans la bande de 2.3 à 3.5kHz, et ceci pour chacune des nuances indiquées séparément (soit f, mf, mp et pp). La ligne avec les points rouges représente toujours l'exemple après le travail de messa di voce. C'est l'écart entre les deux lignes et non l'ondulation des lignes qui est important.
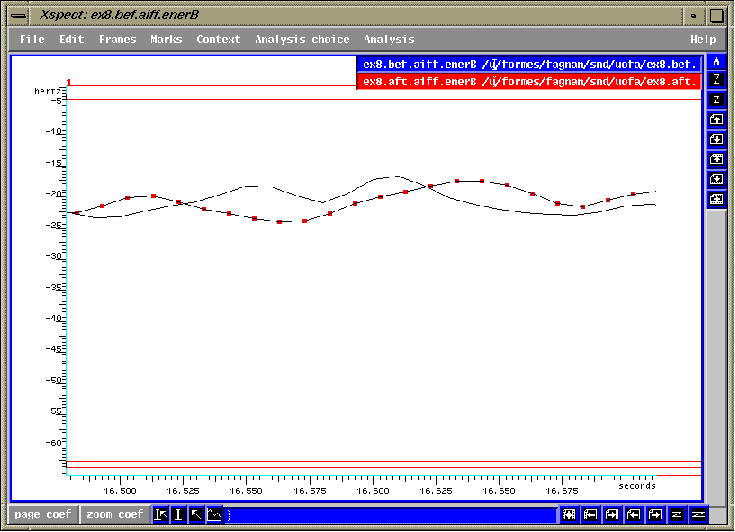
fig.4.2 Portion forte du decrescendo.
Le son n'est pas très différent dans ces deux versions (fig.4.2 et les deux exemples sonores ci-dessous) car le choeur était capable de chanter avec une bonne énergie vocale dans leur son forte. Nous voyons d'après cette analyse que l'ensemble chante au même niveau et avec le même montant d'énergie dans cette bande de 2.3 à 3.5kHz. Nous pouvons cependant déjà entendre une voyelle plus complète et une amélioration de timbre dans la deuxième version.
***EXEMPLE SONORE
(Portion forte avant)***
***EXEMPLE SONORE
(Portion forte après)***
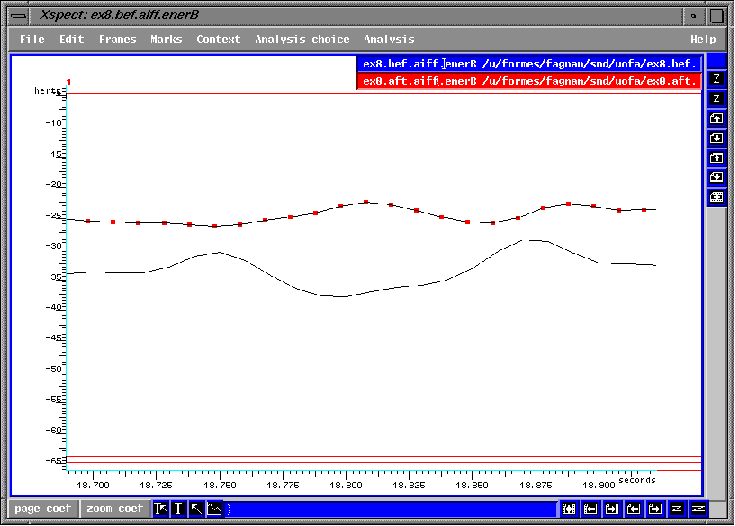
fig.4.3 Mezzo forte
Mezzo forte: Après avoir travaillé le principe
de messa di voce, l'ensemble conserve 8.7dB plus d'énergie 4.3).
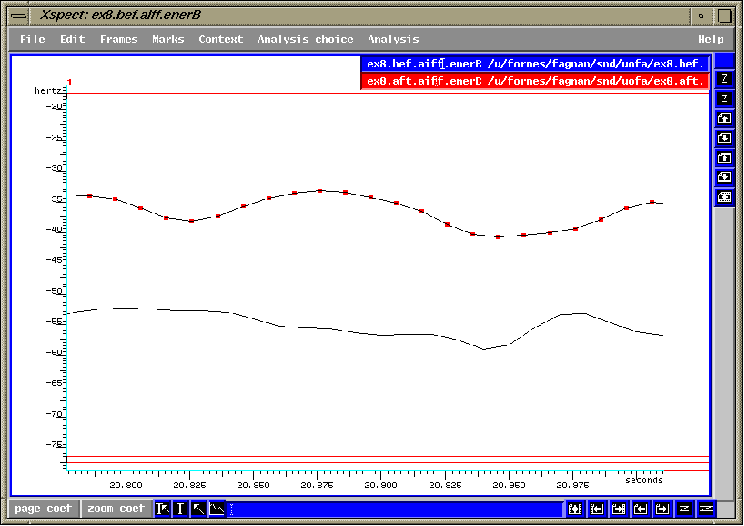
fig.4.4 Un écart de 18 dB dans la portion
mezzo piano.
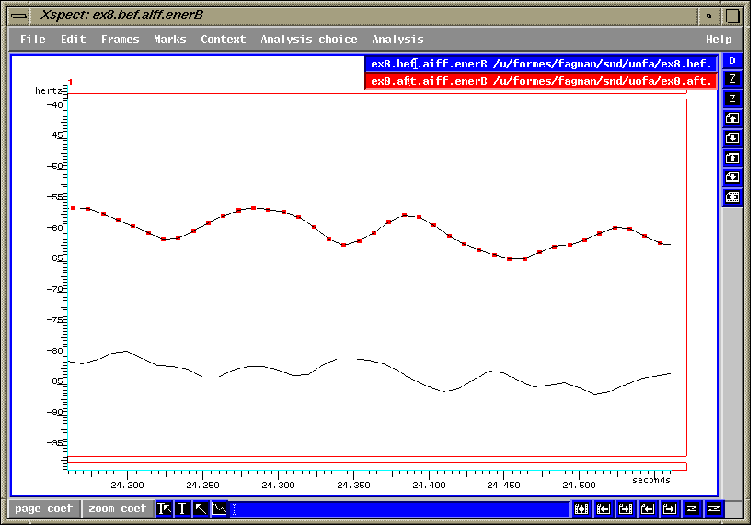
fig.4.5 Pianissimo; Un écart de 22dB
.
***EXEMPLE SONORE
(portion pianissimo avant)***
***EXEMPLE SONORE
(portion pianissimo après)***
Il est évident par cet
exemple que le principe de messa di voce aide à conserver de
plus en plus d'énergie quand l'on chante de plus en plus doucement.
L'efficacité vocale et acoustique présente dans la version
bel canto devient d'autant plus évidente lorsque nous considérons
que les deux exemples ont débutés à la même intensité
dans le forte.
Dans des articles portant sur
l'acoustique des choeurs, on remarque souvent que les ensembles vocaux perdent
énormément d'énergie vocale dans les nuances douces.
Nos résultats semblent montrer que l'application de ce principe central
de la méthode bel canto peut servir à renverser cette
tendance.
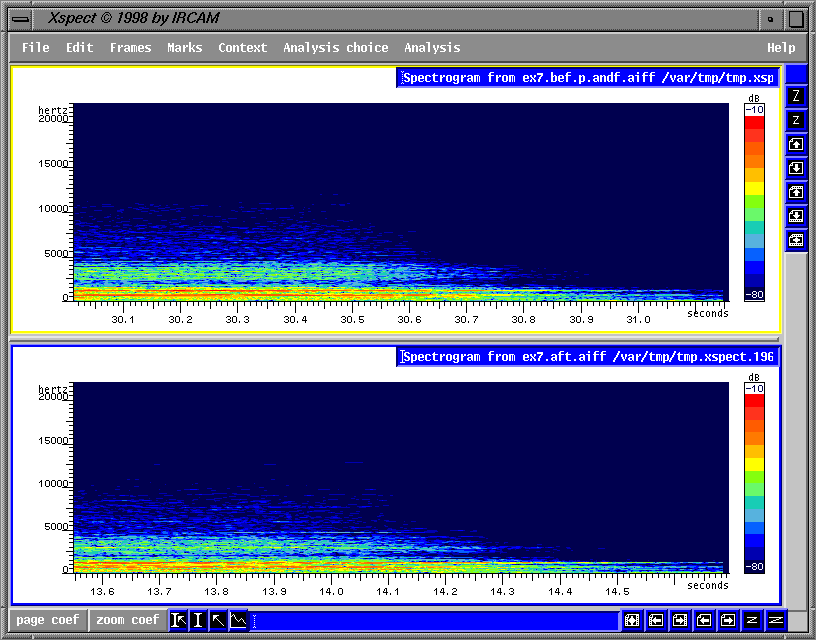
fig.5.1 Chorale mixte - la toute
fin d'un accord à quatre sons.
***EXEMPLE SONORE avant
***
***EXEMPLE SONORE apres
***
Il y a une différence
remarquable dans la façon dont la salle ajoute de la réverbération
à l'énergie augmentée de la deuxième tentative.
On entend aussi que la justesse globale du groupe est beaucoup améliorée
à la fin de cet exemple puisque les chanteurs conservent une voyelle
chiaroscuro et une vibration complète jusqu'à la fin
de l'accord et terminent avec une inspiration plutôt qu'une expiration.
Ces éléments importants de la nota mentale assurent
que la vibration des cordes vocales ne soit pas interrompue et que la fin
de la note ait un maximum d'énergie. Toutefois, ce sont des
subtilités qui sont difficiles à mesurer.
Donc, il existe encore parfois
un écart entre ce que nous entendons et ce que nous pouvons montrer.
b) Le vibrato d'un choeur. Puisqu'un ensemble vocal comprend
plusieurs choristes qui chantent ensemble, il y a plusieurs vibratos différents
qui agissent différemment en temps et en amplitude simultanément.
Il est toujours difficile d'isoler le vibrato et le rôle qu'il joue
dans le chant choral. Nous pourrions toujours demander aux choristes
de chanter sans vibrato, mais ceci engendrerait d'autres changement vocaux
par conséquent. Une étude portant sur le rôle du
vibrato dans le chant choral et son effet sur la justesse d'un choeur serait
donc souhaitable à l'avenir.
Notes:
1. Sten Ternstrom et al. "Articulatory F0
Perturbations and Auditory Feedback." Journal of Speech and Hearing Research
, 31 (June, 1988), 190.
Sten Ternstrom. "Physical and Acoustic Factors that
Interact with the Singer to Produce Choral Sound." Journal of Voice
, 5,2 (1991)137,8.