

Next: RBF neural networks
Up:
RBF Networks for
Previous: Introduction
Assume an n-dimensional dynamical system  evolving on an
attractor A. A has fractal dimension d, which often is
considerably smaller then n. The system state
evolving on an
attractor A. A has fractal dimension d, which often is
considerably smaller then n. The system state 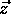 is
observed through a sequence of measurements
is
observed through a sequence of measurements 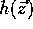 ,
resulting in a time series of measurements
,
resulting in a time series of measurements 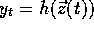 . Under weak assumptions concerning
. Under weak assumptions concerning  and
and  the fractal embedding
theorem[6] ensures that, for
the fractal embedding
theorem[6] ensures that, for 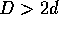 , the
set of all delayed coordinate vectors
, the
set of all delayed coordinate vectors
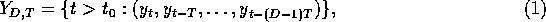
with an arbitrary delay time TT , forms an embedding of A in the
DD -dimensional reconstruction space. We call the minimal DD ,
which yields an embedding of A, the embedding dimension
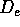 . Because an embedding preserves characteristic features of
A, especially it is one to one, it may be employed for building a
system model. For this purpose the reconstruction of the attractor is
used to uniquely identify the systems state thereby establishing the
possibility of uniquely predicting the systems evolution. The
prediction function may be represented by a hyperplane over the
attractor in an
. Because an embedding preserves characteristic features of
A, especially it is one to one, it may be employed for building a
system model. For this purpose the reconstruction of the attractor is
used to uniquely identify the systems state thereby establishing the
possibility of uniquely predicting the systems evolution. The
prediction function may be represented by a hyperplane over the
attractor in an 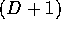 dimensional space. By iterating this
prediction function we obtain a vector valued system model which,
however, is valid only at the respective attractor.
dimensional space. By iterating this
prediction function we obtain a vector valued system model which,
however, is valid only at the respective attractor.
For the reconstruction of instationary systems dynamics we confine
ourselves to the case of slowly varying parameters and model the
instationary system using a sequence of attractors.
Axel Roebel
Thu Nov 9 12:55:11 MET 1995
 evolving on an
attractor A. A has fractal dimension d, which often is
considerably smaller then n. The system state
evolving on an
attractor A. A has fractal dimension d, which often is
considerably smaller then n. The system state 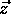 is
observed through a sequence of measurements
is
observed through a sequence of measurements 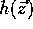 ,
resulting in a time series of measurements
,
resulting in a time series of measurements 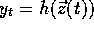 . Under weak assumptions concerning
. Under weak assumptions concerning  and
and  the fractal embedding
theorem[6] ensures that, for
the fractal embedding
theorem[6] ensures that, for 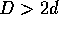 , the
set of all delayed coordinate vectors
, the
set of all delayed coordinate vectors
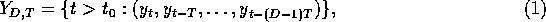
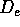 . Because an embedding preserves characteristic features of
A, especially it is one to one, it may be employed for building a
system model. For this purpose the reconstruction of the attractor is
used to uniquely identify the systems state thereby establishing the
possibility of uniquely predicting the systems evolution. The
prediction function may be represented by a hyperplane over the
attractor in an
. Because an embedding preserves characteristic features of
A, especially it is one to one, it may be employed for building a
system model. For this purpose the reconstruction of the attractor is
used to uniquely identify the systems state thereby establishing the
possibility of uniquely predicting the systems evolution. The
prediction function may be represented by a hyperplane over the
attractor in an 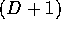 dimensional space. By iterating this
prediction function we obtain a vector valued system model which,
however, is valid only at the respective attractor.
dimensional space. By iterating this
prediction function we obtain a vector valued system model which,
however, is valid only at the respective attractor.