Diemo Schwarz (schwarz@ircam.fr) · Xavier Rodet (rod@ircam.fr)

• Spectral envelopes very useful in sound analysis and synthesis:

• Envelope fit: A spectral envelope is a curve which envelopes the magnitude STS, i.e. it wraps tightly around it, linking the peaks of the sinusoidal partials or passing close to the maxima of non-sinusoidal spectra.
• Smoothness: A certain smoothness of the curve is required: it should not oscillate irratically (fluctuate too wildly over frequency), but give a general idea of the distribution of energy of the signal over frequency.
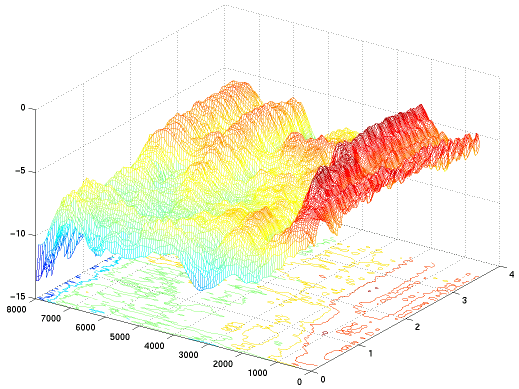
• Adaptation to fast spectrum variations: A spectral envelope is defined relative to a short segment of the signal (typically between 10 and 50 ms). When the STS varies rapidly from one analysis frame to the next, the spectral envelope should follow precisely.

• Robustness: The estimation should yield precise and smooth spectral envelop-es for a wide range of signals with very different characteristics.

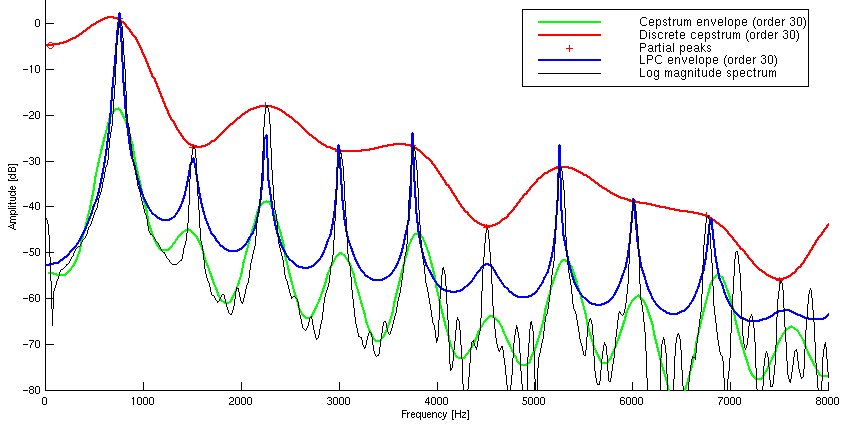
• Linear Predictive Coding: All-pole filter coefficients
• Cepstrum: Smoothes the STS by low-pass filtering of log magnitude. Cepstrum coefficients.
• Discrete Cepstrum: Computed from distinct points in frequency-amplitude plane, e.g. spectral peaks of a STS, sinusoidal partials.
• Improvement of preciseness using a nonlinear frequency scale (e.g. logarithmic or mel scale) reflecting the frequency resolution of the human ear (coarser for high frequencies).

• The figure shows weaknesses of LPC and cepstrum estimation: Both descend down into the space between the partials for high-pitched sounds. Low-order LPC estimation is too smooth. Cepstrum averages the spectrum, does not link the peaks either.
• These problems are avoided by the discrete cepstrum method. Nevertheless, LPC and cepstrum are still very well applicable to the residual noise, where the discrete cepstrum cannot be used.
• Improvement of robustness of estimation using a composite envelope: discrete-cepstrum from voiced part below maximum voiced frequency, LPC above [1][2].

• Preciseness: Describe an arbitrary spectral envelope (from estimation or given manually) as precisely as possible.
• Stability: Small changes, e.g. noise, must not lead to large changes in representation, but must result in equally small changes
• Locality in frequency: Achieve a local change of a spectral envelope by simple change in parameters.
• Flexibility and ease of manipulation: Allow various manipulations, easy to specify, with exactly defined desired outcome, effect on spectrum easily understood.
• Speed of synthesis: Representation usable for synthesis as directly as possible, without first converting to a different form at high computational costs.
• Space in memory: The representation must not take up too much space.
• Manual input: The representation should be easy to specify manually or by textual input of parameters.

• Filter coefficients: Cepstrum or one of the several types of LPC coefficients.
• Sampled representation: The spectral envelope is sampled at n frequency points, equidistant or nonlinearly spaced.
• Geometric representations: Piece-wise linear, splines (quadratic or cubic interpolation), points placed on the maxima, minima, and inflection points of the envelope.
• Formants: Resonances in a resonator (vocal tract), maxima of the spectral envelope. Combine by multiplication or addition, serial or parallel structure of synthesis filters.
• Formant waveforms (FOFs): Represent a formant as an elementary wave-form. FOFs add up to build spectrum.
• Basic formants: A simpler way to describe formants of a spectral envelope using the parameters center frequency, amplitude and bandwidth and addition.
• Fuzzy formants: Approximate locations of formants as regions within a sampled spectral envelope where a formant is assumed to exist.

• Filtering: The spectral envelope has to be converted to filter coefficients for time-domain filtering, or to a transfer function for frequency-domain filtering (e.g. with SuperVP).
• Additive synthesis: Sum of sinusoidal partials with amplitudes according to the sinusoidal spectral envelope and of a residual noise the spectral density of which is given by the noise spectral envelope (filtering white gaussian noise)
• FFT^-1 method of additive synthesis: Allows a speed gain of 10 to 30. Applying the sinusoidal spectral envelope is straightforward. Synthesizing residual according to the noise spectral envelope is easy and inexpensive: just add random values in the desired frequency bins.

• The proposed high-level approach to spectral envelopes can simplify the problem of controlling sinusoidal partials for additive synthesis, and manipulating them in a sensible way [3].

• Spectral envelopes are necessary for modification and synthesis of the singing voice in a sensible manner.
• Many aspects of the expressivity of the singing voice depend on the spectral envelope (e.g. spectral tilt).
• A new type of high quality singing voice synthesis is possible:

• Spectral envelopes allow to influence the timbre of a sound to a great degree, composers can obtain a desired effect by the use of high-level representations.
• To the performer, the real-time application of spectral envelope manipulation greatly enhances expressivity through easily understandable and "musical" parameters.
• Each representation has its strong points

  -> use and combine all of them in an object-oriented class hierarchy.

  • All the programs developed at Ircam use the standardized, open, and extensible Sound Description Interchange Format (SDIF) [6][7] to facilitate the exchange of data with well-defined semantics between programs, hardware architectures, and institutions. With more and more analysis-synthesis tools being ported to SDIF, this will create important synergetic effects in research and creation.
  • See also the chapter Spectral Envelopes and Additive+Residual Analysis-Synthesis in the forthcoming book The Sound of Music, J. Beauchamp editor.

  ---

  Bibliography

  [1] Y. Stylianou, J. Laroche, E. Moulines. High Quality Speech Modification based on a Harmonic+Noise Model. Proc. EUROSPEECH, 1995.

  [2] Marine Campedel-Oudot. Étude du modèle sinusoides et bruit pour le traitement de la parole. Estimation robuste de l'enveloppe spectrale. Thèse, ENST, Paris, 1998.

  [3] A. Freed, X. Rodet, Ph. Depalle. Synthesis and Control of Hundreds of Sinusoidal Partials on a Desktop Computer without Custom Hardware. ICSPAT, 1992.

  [4] Diemo Schwarz. Spectral Envelopes in Sound Analysis and Synthesis. Diplomarbeit, Universität Stuttgart, Fakultät Informatik, Germany, 1998.

  [5] F. Déchelle, M. DeCecco, E. Maggi, N. Schnell. jMax Recent Developments. Proc. ICMC, 1999.

  [6] Dominique Virolle, Diemo Schwarz. Xavier Rodet. Sound Description Interchange Format. Web page. http://www.ircam.fr/sdif

  [7] M. Wright, A. Chaudhary, A. Freed, S. Khoury, D. Wessel. Audio Applications of the Sound Description Interchange Format Standard. AES 107^th convention, 1999.