Published in: Proceedings of the ICMC 2001, Havana, Cuba. Revised version, October 12, 2001 - Fri Oct 12 15:56:06 CEST 2001

Alignment of Monophonic and Polyphonic Music to a Score

Nicola Orio Diemo Schwarz

Abstract

Music alignment is the association of events in a score with points in the time axis of an audio signal. The signal is thus segmented according to the events in the score. We propose a new methodology for automatic alignment based on dynamic time warping, where the spectral peak structure is used to compute the local distance, enhanced by a model of attacks and of silence. The methodology can cope with performances considered difficult to align, like polyphonic music, trills, fast sequences, or multi-instrument music. An optimisation of the representation of the alignment path makes the method applicable to long sound files, so that unit databases can be fully automatically segmented and labeled. On 708 sequences of synthesised music, we achieved an average offset of 25 ms and an error rate of 2.5%.

1 Introduction

Music alignment is the association of events in a musical score (in our case, notes) with points in the time axis of an audio signal. The signal is a digital recording of the score being played by musicians and is referred to as the performance. An alignment implies a segmentation of the performance according to the events in the score.

We propose a new methodology for automatic alignment based on dynamic time warping (DTW). The spectral peak structure is used as the main feature for computing the local distance between frames of the performance and elements in the score. Additional features model silences and note attacks. The methodology can cope with polyphonic and multi-instrument performances as well as with performances where fast sequences or trills are present. Normally, blind segmentation methods [Rossignol 2000], which only use the information from the audio signal, are not very accurate with these kinds of performances.

1.1 Applications

A great part of the research in computer science is devoted to the automation of processes carried out by humans. Automatic processes are particularly useful in a number of situations. For instance, the segmentation of a large collection of recordings, which may last several hours, can not feasibly be done manually because of the large amount of data. The same situation applies for difficult signals (i.e., fast sequences of notes with legato) where manual segmentation may be tedious or imprecise.

Automatic alignment of music sequences has a number of applications, the most important being:

1. Segmentation of a performance into notes and labeling (tagging) of the notes with the information from the score for building unit databases [Schwarz 2000]. Along with the note pitch and length, there can be additional symbolic information attached to the score, such as dynamics, articulation, or lyrics.

2. Comparison of different performances for musicological research, for instance aimed at the study of the expressive parameters related to timing.

3. Indexing of continuous media through segmentation for content-based retrieval. The total alignment cost between pairs of documents can be considered as a distance measure (as in early works on speech recognition), allowing to find the best matching documents from a database.

Alignment is related to the problem of real-time synchronisation between performers and computers, usually called score following, when additional constraints of low-latency and only local knowledge of the performance are introduced. Off-line alignment can be used as a bootstrap procedure for the training of real-time statistical models.

1.2 Previous Work

Automatic alignment of sequences has been a popular research topic in many fields, such as string analysis, molecular biology, and notably speech recognition. The literature is considerably vast, and we only mention two comprehensive overviews on the different approaches in speech recognition [Rabiner and Juang 1993] and in biological sequence analysis [Durbin et al. 1998].

An interesting work on music alignment is [Raphael 1999]. Alignment is computed through the use of a hidden Markov model (HMM), and can be performed both on-line for score following, which is the primary goal, and off-line for segmentation. HMMs can be seen as an appealing alternative to DTW, in particular because they can be trained. However, for pairwise alignment of sequences, which is our goal, HMMs and DTW are two completely interchangable techniques [Durbin et al. 1998]. Our choice of DTW is due to the possibilty to optimise memory requirements for large soundfiles, as presented in section 2.3. Refer to the parallel paper [Orio and Déchelle 2001] for the use of HMMs in on-line score following.

Alignment has also been used in speech synthesis research, as a useful tool for preparing unit databases for concatenative speech synthesis. The results of the MBROLIGN technique from the MBROLA project [Malfrère and Dutoit 1997], has been the motivation for our methodology.

2 The Methodology

Alignment is carried out using DTW. This technique finds the best global alignment of two sequences, based on local distances. It uses a Viterbi path finding algorithm that minimizes the global distances between the sequences.

The sequences to be aligned consist of frames containing features. The feature data for the performance are extracted by signal analysis techniques. The feature data for the score are generated for each frame according to a model of the instrument. In our case, the model is a simple harmonic spectrum that is constant for each note, together with a model of the attack and a model for the silence. The temporal resolution of the alignment is given by the performance frame rate. For instance, a hopsize of the analysis window of 256 points gives a resolution of 5.8 ms at a sampling rate of 44.1 kHz. The score frame rate can be much lower than the performance frame rate, saving computation time and memory storage, because DTW is robust to differences in the lengths of the two sequences.

2.1 Calculation of Local Distances

The local distances are calculated for each pair of a frame m in the performance and a frame n in the score. They are represented as the local distance matrix d(m, n). Only a part of the matrix needs to be calculated, because local and global path constraints reduce the number of points {m, n} that can be part of the optimal path [Rabiner and Juang 1993].

2.1.1 Peak Structure Distance (PSD)

The principal feature for segmentation of musical signals is pitch (as opposed to spectral envelope for speech). However, pitch tracking is still error prone, even more so for polyphonic signals. This is why we do not use pitch as a feature directly, but the structure of the peaks in the spectrum given by the harmonic sinusoidal partials. This extends well to polyphonic signals.

The expected peaks are modeled from the pitches in the score: For each note running at a certain score frame, h harmonic peaks are generated. After a number of tests, we chose h=8 but good results can be obtained also with smaller values. The peaks take the form of rectangular spectral bands with an equal amplitude of 1 in an otherwise zero spectrum. Figure 1 shows a set of filters together with two signals, representing small and big distances. Each band has a bandwidth of one half-tone to accommodate for slight tuning differences and vibrato. This generated score spectrum S is multiplied by the Fourier magnitude spectrum P² of one frame of the performance. If the peak structures of the two frames are close, the sum of this product will be high. We can also see this procedure as filtering.

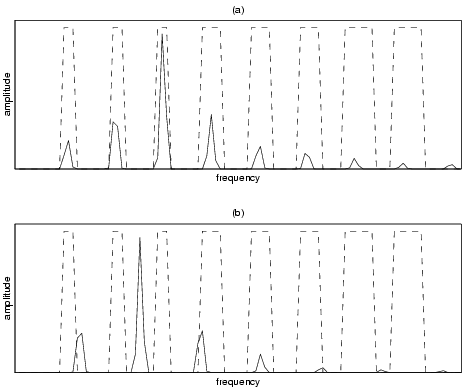
Figure 1: The generated spectral bands with a good (a), and a bad (b) matching performance spectrum.

Normalization of the results of || S · P² || is necessary to prevent a loud, noisy frame from matching all generated bands. To this aim, its value is divided by the signal energy in the frequency range that contains all the rectangular spectral bands.

The definition of the peak structure distance is thus

PSD(m, n) = 1 -

S_i P_i²

P_i²

(1)

with [m, n] respectively the frames in the performance and in the score, and i the FFT bins. The calculation of the product S_i P_i² for the PSD can be implemented very efficiently by summing the bins of P² within the bands.

2.1.2 Delta of Peak Structure Distance (DPSD)

Tests using the PSD highlighted that alignment marks are sometimes set too late. The two reasons are that, first, reverberation causes the partials of the last note to still be present at the start of the next note, and secondly, that during the attacks of musical instruments, energy is often spread all over the spectrum, giving low values of the PSD.

However, the energy at the peaks of the expected note rises sharply during the attack. Hence, we can get a more accurate indication of the start of a note, using the delta of PSD. The distance DPSD is given by clipping d below a threshold q_d:

DPSD(m, n) =

ì
í
î

d - q_d	if d ³ q_d
0	if d < q_d

(2)

with d = PSD(m, n) - PSD(m-1, n). Clipping is necessary to prevent negative distance values.

2.1.3 Modeling of Silence

We introduce special score frames at the end of each note to correctly handle possible silence caused by rests in the score or by non-legato playing styles. For these frames, a special distance sPSD measures the match of the signal log energy e above a silence threshold q_s.

sPSD(m, n) =

ì
í
î

e - q_s	if e ³ q_s
0	if e < q_s

(3)

with e = log å P_i². This allows the alignment path to stay in the silence frame in the score and advance in the performance in order to ``stretch out'' the pauses between notes.

2.2 Dynamic Time Warping

DTW is a consolidated technique for the alignment of speech sequences, the reader may refer to [Rabiner and Juang 1993] for a tutorial. Using dynamic programming, DTW finds the best alignment between two sequences according to a number of constraints. The alignment is given in the form of a path in the local distance matrix. If a path goes through [m, n], the frame m of the performance is aligned with frame n of the score.

The following constraints have been applied: The end points are set to be [1, 1] and [M, N], where M and N are the number of frames of the performance and of the score, respectively. The path is monotonic in both dimensions. Among the different local continuity constraints, the simplest one gave the best results.

The best path is computed iteratively, given the initial condition p(1, 1) = d(1, 1):

p(m, n) = min

{

3 p(m-1, n-1) + 2 d(m, n) p(m-1, n)+d(m, n) p(m, n-1)+d(m, n)

}

(4)

where p(m,n) is the cost for a path up to the point [m, n]. The local distance d is given by

d(m, n) =

ì
í
î

s_d DPSD(m, n)	if n Î A
s_s sPSD(m, n)	if n Î S
PSD (m, n)	otherwise

(5)

where s_d and s_s are scaling factors to bring the values into the range of PSD, and A and S are the first and last frames of all notes, respectively.

2.3 Implementation Considerations

The DTW algorithm can be implemented efficiently such that the performance need not be present in memory as a whole. Equally, the distance matrices are accessed only in the neighbourhood of the current performance frame, so that only the last two lines of these need to be kept in memory. However, the matrix that stores all possible paths can not be reduced, because we only know at the end which path is the optimal one.

This poses memory problems for the fully automated application of DTW on real-world sound files. As an example, the first movement of the Sonata 1 for solo violin by J.S. Bach lasts 2 1/2 minutes and contains 450 notes. This yields about 24000 frames for the performance and the score, and matrices of around 0.5 · 10⁹ elements, taking up at least 2 GB of memory. A global path constraint, i.e. considering only a central corridor for the possible paths, reduces the memory requirement by only a factor of 2, leaving it still too high for today's computers.

However, all we are interested in is the alignment of note onset times. We don't care about (and indeed didn't model) the evolution within a note. This means that we only need to keep in memory all possible shortcut paths, i.e. paths that are reduced to the first and last score frame for each note. Their memory requirement is only 10⁷ elements, i.e. 40 MB.

3 Results

The results of our method are very encouraging. We tested recordings of various monophonic and polyphonic acoustic instruments with very good results. Even very difficult signals, such as held chords with only one changing note, very fast violin passages (e.g. 16 legato notes at a rate of 10 notes per second with irregular accents), and performances with trills and vibrato were perfectly aligned. Preliminary tests on multi-instrument music (a string and oboe quartet) showed a good global alignment with an imprecision of a few frames in the determination of the note onsets.

Quantitative tests have been carried out on 708 performances played by a sample based synthesizer. The choice of synthesized sounds provides a reference of note onsets in the performance, without requiring a manual alignment. We used 14 different sounds, played with the 4 different levels of articulation legato (l), detaché (d), pause (p), and staccato (s), with gradually longer silence. We prepared six different scores, three monophonic, two with two voices of polyphony, and one with three voices of polyphony. Among the monophonic scores, one is a simple repetition of the same note, and one is deliberately mismatched with its performances by one octave to test the robustness of the algorithm. The scores were played at 3 different transpositions, each 2 octaves apart.

We had to eliminate the results given by one of the sounds, because it was a bell whose inharmonic spectrum is not modeled by our technique. The results for the octave-mismatched score were encouraging, but the robustness on octave deviations has still to be extensively tested. As we expected, our technique is not very suitable for the performances with repeated pitch, because the peak structure does not change between notes. The technique needs to be improved by using other features for dealing with this special case.

In the following sections we present the quantitative analyses on the remaining 480 examples.

3.1 Error Rate

We considered an error an alignment mark more than 200 ms off of the expected performance position. Of all the files, only 9.4% had erroneous marks at all (11.9% without the attack and silence modeling). For monophonic performances, this rate drops to 2.5%. The percentage of alignment errors over all marks in all performances is 2.5% (0.42% for the monophonic, 3.6% for the polyphonic performances).

The error rate is lowest for the middle octave, and drops with the introduction of longer pauses. However, for the staccato playing style, we noticed a small increase of the error rate. The same effect was noticed when only the PSD was used.

3.2 Offset

A more detailed parameter is the average offset (i.e. the absolute distance between the expected and found alignment mark) on non erroneous marks.

As can be seen in table 1, there is a decrease of the offset for higher octaves, due to the larger window size needed to resolve low frequency spectral peaks. Moreover, the offset generally decreases with longer pauses, with the exception of the lowest octave.

mono low mid high avg

l 44 33 26 34

d 20 16 8 15

p 35 11 8 18

s 37 10 9 19

avg 34 18 13 23

poly low mid high avg

l 58 36 35 43

d 26 18 15 20

p 33 13 7 18

s 35 10 9 18

avg 38 19 16 26

Table 1: Average offset in ms depending on articulation and octave, for monophonic and polyphonic scores.

Regarding the comparatively high offsets for legato articulation, listening to the found segments revealed that the algorithm chose to place the note onset where the overlapping partials of the previous note had sufficiently died down, which is actually better suitable for the application of building unit databases.

When the alignment is computed without the attack and silence modeling, the average offset is 31 ms, which if compared to the total average of the complete modeling of 25 ms, justifies its higher complexity.

4 Conclusions and Future Work

Our method can cope with difficult signals, such as polyphonic music, multi-instrument music, trills, vibrato, and very fast sequences.

One fundamental problem restricts the choice of features for alignment: It is difficult to generate good expected values from the score that match the feature values of the performance. This is due to problems of scaling and normalization, and, more difficultly, to the need of a model of the instrument and the performer, see [Dannenberg and Derenyi 1998].

High-quality automatic alignment will be used for concatenative sound synthesis based on unit selection [Schwarz 2000]. The necessary unit databases are prepared by our alignment method by segmenting and labeling classical music recordings for which scores in the form of MIDI files exist.

The accuracy of the alignment is limited by the hopsize and suffers from an incertainity within the window. For staccato performances, we can significantly improve the offset by reanalysing the found frame with a simple but precise energy-based onset detector. For other performances, the accuracy will not be affected.

We are currently working on a totally automatic system, which uses MIDI files as reference scores and a database of recordings. To this end, we will develop a technique for the automatic scaling of the system parameters, based on a preprocessing of the performances. The preprocessing will give information about the general features of the recordings, like range of amplitudes for the modeling of silence and potential peak position for the tuning of the filter banks.

References

[Dannenberg and Derenyi 1998]: Dannenberg, R. B. and I. Derenyi (1998, September). Combining Instrument and Performance Models for High-Quality Music Synthesis. Journal of New Music Research 27(3), 211--238.
[Durbin et al. 1998]: Durbin, R. et al. (1998). Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press.
[Malfrère and Dutoit 1997]: Malfrère, F. and T. Dutoit (1997). Speech Synthesis for Text-To-Speech Alignment and Prosodic Feature Extraction. In Proc. ISCAS 97, Hong-Kong, pp. 2637--2640.
[Orio and Déchelle 2001]: Orio, N. and F. Déchelle (2001). Score Following Using Spectral Analysis and Hidden Markov Models. In Proceedings of the ICMC, Havana, Cuba.
[Rabiner and Juang 1993]: Rabiner, L. R. and B.-H. Juang (1993). Fundamentals of Speech Recognition. Englewood Cliffs, NJ: Prentice Hall.
[Raphael 1999]: Raphael, C. (1999). Automatic Segmentation of Acoustic Musical Signals Using Hidden Markov Models. IEEE Transactions on Pattern Analysis and Machine Intelligence 21(4), 360--370.
[Rossignol 2000]: Rossignol, S. (2000, July). Segmentation et indexation des signaux sonores musicaux. Ph. D. thesis, Université Paris VI.
[Schwarz 2000]: Schwarz, D. (2000, December). A System for Data-Driven Concatenative Sound Synthesis. In Digital Audio Effects (DAFx), Verona, Italy, pp. 97--102.

This document was translated from L^AT_EX by H^EV^EA.