La guerre des lapins

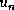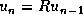Dans un grand domaine, des lapins s'ébattent librement. Les premières années, leur taux d'accroissement annuel est à peu près égal à une constante R, comprise entre 1 et 4. Autrement dit, la population passe d'une année sur l'autre de à . On suppose que la population initiale est de 500 lapins.

• Donner la loi d'évolution de la population de lapin [rsolve].
• Dans quels cas est-elle divergente? Dans quels cas cette suite est-elle convergente. Quelle est sa limite?

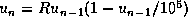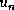Mais plus la population augmente, plus les ressources en nourriture diminuent, ce qui réduit l'accroissement de population. Finalement les démographes lapins constatent que l'évolution de la population respecte la loi: à ceci près que le nombre est entier (il prend la valeur entière immédiatement inférieur [floor]). Autrement dit, plus 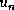se rapproche de l'effectif 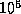, plus le taux de croissance diminue.

• Programmer la procédure u qui permet de calculer .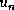
• Représenter graphiquement l'évolution de la population sur 100 ans quand R vaut successivement 1.005, 1.1, 2.95, 3.05, 3.336 et 3.56, 3.57, 3.58, puis enfin 4. Dans le cas où la population n'est pas constante, évaluer la périodicité de cette suite (si tant est qu'elle est périodique) pour chacune de ces valeurs.

Nous allons tenter de prévoir pour quelques cas le comportement à long terme de l'évolution de la population.

• Dans l'hypothèse où la suite 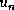est convergente, on note 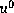sa limite. Calculer 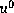en fonction de R (on admettra que la suite est convergente quand ).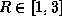
• On suppose à présent que la suite oscille entre deux valeurs (autrement dit, que les suites extraites de rang respectivement pair et impair convergent vers deux limites différentes notés 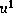et 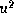). Calculer 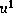et 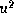en fonction de R.