Exemple

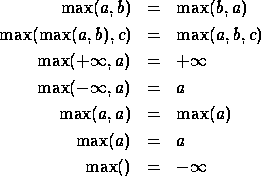
Voyons par exemple comment nous pourrions définir la fonction max définie par les propriétés suivantes:

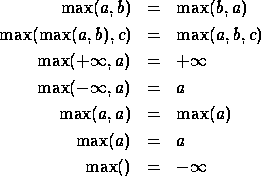
max := proc() local a;
  a := {args};
  if member(infinity,a) then RETURN(infinity) fi;
  a := map(
    proc(x) if type(x,function) and op(0,x) = max then op(x) else x fi end,
    a);
  a := map (
    proc(x) if x<> -infinity then x fi end, 
    a);
  if nops(a) = 0 then RETURN(-infinity) fi;
  if nops(a) = 1 then RETURN(op(1,a)) fi;
  'max'(op(a))
end;

La première commande a:={args}; permet d'implémenter la commutativité et d'éliminer les termes de multiplicité supérieure à un. La seconde implémente la propriété . La troisième commande implémente la propriété en évaluant toutes les occurances de max a ses propres arguments. La quatrième commande supprime toutes les occurances de dans la liste des arguments. Les deux commandes suivantes évaluent max dans le cas où il ne reste plus que un ou aucun argument. La dernière commande renvoie 'max'(op(a)) sans l'évaluer.

Le comportement de la fonction max correspond dans un premier temps à une série de simplifications de l'expression passée en argument, et le cas échéant au retour de l'expression originale sans vraiment l'évaluer. C'est un comportement très standart en programmation MAPLE, (et très différents des autres styles de programmation). La plupart des fonctions de MAPLE (sin, exp, ...) se contentent de faire des manipulations de l'expression passée en argument quand c'est possible, et renvoie l'expression originale sans évaluation par défaut. Dans le cas de sin, le système vérifie si l'argument est une expression connue en (si multiple entier de alors 0, si alors , etc), puis tente de ramener l'expression dans l'intervalle , puis si l'expression est négative, sort le - du sinus...Si aucunes de ces manipulations n'aboutissent, le système renvoie 'sin'(op(a)), c'est à dire qu'il dit: . En fait, c'est uniquement au moment de l'évaluation numérique (dans la fonction `evalf/sin`()) que sin fait réellement quelque chose, c'est-à-dire renvoie une valeur numérique.

        Pour résumer, les propriétés intrinsèques d'une fonction f sont décrites dans la définition de la procédure MAPLE f. Les propriétés de f vis à vis des autres fonctions sont décrites dans la famille de fonctions simplify et convert. Les évaluations numériques sont assurées par la fonction evalf/f. La dérivée de la fonction se retrouve dans diff/f; la primitive . Je ne sais pas encore comment sont codés les primitives et les methodes d'intégration pour la fonction f.