1. Principe général

On voudrait aborder la problématique du traitement du son sous l’angle dynamique — c’est à dire que l’on s’intéresse plus particulièrement à l’évolution temporelle du traitement et de ses paramètres.

Le premier aspect relatif à cette approche concerne le problème du contrôle, au sens général du terme : contrôle manuel, contrôle en référence à des trajectoires prédéfinies, évolution du contrôle…

Soit donc au départ une évolution linéaire d’un paramètre.

Cette évolution est linéaire ou comporte un aspect linéaire important si elle est dessinée a priori ou réalisée en temps réel par un utilisateur, qui aura naturellement tendance à lui donner une forme linéaire, en tous cas une forme qui ne sera pas forcément " perceptivement adaptée ", ou, disons " perceptivement optimisée ".

Par ailleurs, si l’on se réfère aux outils de traitement que l’on trouve dans le commerce et qui comportent un aspect dynamique, comme les plug-ins GRM Tools ou le logiciel ProTools (automation des effets ), on constate que l’évolution des paramètres de traitement se base toujours sur des forme à caractère linéaire — une exception : la version 5 de ProTools, mais la méthode utilisée, en plus d’être très sommaire, n’est pas un succès.

Cette évolution est donc quantitativement linéaire.

La première étape consiste à lui donner un aspect perceptivement linéaire, ce qui est un problème de psychoacoustique classique.
C’est ce qu’on appelle par la suite la " linéarisation à grande échelle " - échelle qui sera en fait notre échelle de référence dans toute la suite

La seconde étape consiste à adapter cette évolution à la perception. Pour cela, il est nécessaire que la forme suivie par cette évolution comporte des informations à plus d’une échelle. Comme on parle ici de contrôle, on peut supposer que les formes à l’échelle supérieure seront apportées par l’utilisateur.
On travaille alors sur les plus petites échelles. C’est ce qu’on appellera " délinéarisation à petite échelle ".

Par ailleurs, on peut souhaiter agir sur plusieurs paramètres en même temps, dans le but de réaliser une transformation plus riche. Il faut donc alors rassembler les paramètres indépendants en un seul paramètre, qui deviendra le paramètre de contrôle de cette nouvelle évolution.
C’est ce qu’on désignera par " rassemblement des paramètres ".

La problématique est finalement d’ordre plus général, et peut se résumer ainsi : comment rendre un son plus vivant, plus adapté à la perception, qu’il ne l’est au départ ? On utilise alors les trois mêmes méthodes : linéarisation à grande échelle, délinéarisation à petite échelle, rassemblement des paramètres.

  2. Un générateur de formes

Si l’on souhaite pratiquer la " délinéarisation à petite échelle ", il convient de mettre au point un générateur de formes. Ces formes seront ensuite, d’une manière ou d’une autre, associées à la transformation ou l’évolution du son à petite échelle.

Voici quatre formes que l’on utilisera couramment ; par ordre de périodicité croissante :

* Forme 1 : tirage aléatoire avec probabilités uniformes (random simple)

Note concernant la forme 3 : le système de Lorenz possède un comportement de type " chaos déterministe " - il est défini par un système de 3 équations différentielles :

X’(t) = a(X(t) — Y(t)) Y’(t) = -X(t)Z(t) — ReynoldsNumberX(t) Z’(t) = X(t)Y(t) — bZ(t)

3. Première expérience : cas d’école

1. fréquence de coupure lowpass de 30Hz à bypass
2. directivité cube de omnidirectionnel à bidirectionnel

0. [ Ecoute des deux évolutions ]
1. liaison des deux évolutions — création, donc, d’un " paramètre global " ou " rassemblé "
2. idem + linéarisations à grande échelle des deux évolutions
3. idem + délinéarisation petite échelle

Résultats de l’expérience :

Etape 1 (rassemblement des deux évolutions en une seule = rassemblement des paramètres) : Malgré la différence de nature des deux évolutions, on ne perçoit plus chaque évolution en tant que telle, mais on perçoit une évolution unique. Dans ce cas là au moins, la notion de rassemblement des paramètres s’applique fort bien. Par contre, l’évolution elle même n’est pas du tout progressive : on passe brutalement d’un état à un autre, sans bien comprendre la transition.  

Etape 2 (linéarisation à grande échelle) : On résout le problème précédent en modifiant la forme chacune des évolutions individuelles. La fonction de transfert est, dans le cas du paramètre individuel lié à GRM bandpass, de type exponentielle, tandis que dans le cas de la directivité du la source, elle est de plutôt de type logarithmique.  

Etape 3 (délinéarisation à petite échelle) : Une fois l’ " évolution rassemblée " régulière, on applique à ce paramètre une délinéarisation à petite échelle réalisée avec la forme 4 du générateur de forme. On finit par trouver un " taux de délinéarisation " pour lequel on n’entend plus cette perturbation en tant que telle, mais pour lequel on entend la même évolution globale, mais d’aspect plus " naturel " : on la perçoit comme une évolution , certes, mais plus comme un glissendo de paramètres à l’aspect rectiligne.

Conclusion : L’application des principes évoqués lors du paragraphe 1 du même chapitre semble donc, au moins pour ce cas relativement simple, un succès.    

4. Composante à petite échelle : une expérience

Penchons nous maintenant de manière plus détaillée sur la délinéarisation à petite échelle.

L’expérience :

Prenons un son, apparemment de synthèse, ressemblant à un son de triangle. Ce son est essentiellement formé d’une attaque, et d’un decay très peu riche à l’échelle des 100ms. A l’audition, ce decay sonne " linéaire " et perceptivement peu intéressant.

L’expérience consiste à appliquer différents vibratos de hauteur à ce decay, afin de déterminer le seuil à partir duquel on n’entend plus cette modulation en tant que vibrato, c’est à dire à partir duquel on entend le son d’origine, enrichi perceptivement à petite échelle.

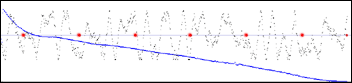
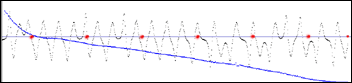
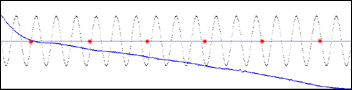
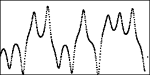
Ce vibrato de hauteur est réalisé à partir du générateur de formes. Les quatre illustrations ci dessous montrent, en bleu, l’enveloppe RMS du son. Les points rouges sur l’axe des temps représentent les secondes. En noir, les formes qui ont été utilisées, à différents taux, pour la modulation.

forme 1	forme 2
forme 3	forme 4

Voici, exprimés en demi-tons crête à crête, puis en rapport de fréquence crête à crête, l’amplitude des différents vibratos appliqués — pour chaque groupe de mesures, on peut voir que l’amplitude diffère d’une forme à l’autre ; ces ajustements, réalisés sur la base d’expériences antérieures, ont pour but d’atténuer les différences concernant l’amplitude de la perturbation perçue lors de l’application d’une même valeur numérique.  

Résultats de l’expérience / conclusions : A l’écoute, on constate les phénomènes suivants :

1. Les formes les plus aptes à la délinéarisation, c’est à dire celles qu’on perçoit le moins en tant que telles, et qui semblent le plus faire partie du son, sont les formes 2 et 3. La forme 1 présente un caractère artificiel très regrettable qui fait immanquablement penser à certains synthétiseurs de la fin des années 70. Quant à la forme 4, elle est trop périodique, et est toujours perçue en tant que telle.
2. L’amplitude " critique ", celle où l’on croit entendre un enrichissement du son plutôt qu’une forme rajoutée, se situe extrêmement près du point où la modulation est tellement faible qu’on n’entend plus ni forme, ni délinéarisation. Dans le cas présent, les seules valeurs correspondant au phénomène recherché sont celles des groupes 4 ou 5, qui témoignent en effet d’une modulation extrêmement faible.

 

Remarque : A la lumière des principes exposés lors du chapitre 1, on peut constater que les formes qui se prêtent bien à une utilisation en tant que composante à petite échelle comportent des informations non immédiatement compréhensibles, c’est à dire de forme ni trop forte, ni trop faible, à au moins deux échelles d’observation distinctes : c’est à dire des formes considérées, à la lumière des principes du chapitre 1, comme " perceptivement adaptées ".  

5. Une expérience complémentaire à la précédente

L’expérience :

Prenons un filtre passe-bas de pente 6dB / octave — le plug-in VST Prosoniq North Pole, et faisons évoluer sa fréquence de coupure du point le plus bas possible — 20Hz, au point le plus haut possible — bypass.         Puis, linéarisons cette évolution à grande échelle : on utilise pour celà une fonction de transfert de type exponentiel. On obtient alors l’évolution suivante — mesurée ici à l’aide un bruit rose:

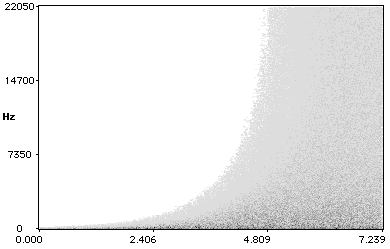
Cette évolution est perçue comme linéaire. On utilise ensuite les mêmes formes que précédemment, dans le but de délinéariser cette évolution à petite échelle. Le son utilisé pour le test est une trame stable à grande échelle, comportant déjà un certain nombre d’informations à petite échelle, très riche spectralement.     Pour chaque forme, on teste donc les valeurs de modulation suivantes — mesurées avec un bruit rose.

1. La valeur du rapport de fréquence crête à crête correspondant à l’effet recherché se situe aux environs de 1.3.
2. Le choix de la forme est ici moins critique que dans le cas précédent : les formes 2 et 3 donnent certes un résultat plus naturel, mais, contrairement à ce qui se passait dans l’expérience précédente, il reste ici possible d’utiliser les formes 1 et 4.

Conclusions : Première constatation : lors de l’expérience précédente, le rapport de fréquence crête à crête de la modulation correspondant à l’effet recherché se trouvait aux alentours de la valeur 1.005, ce qui correspondait à un comma à peine ; ici la valeur typique est plutôt de l’ordre de 1.3 ou 1.4 , ce qui correspond à un intervalle d’environ 5 demi tons. On répète alors la même expérience en utilisant un autre plug-in, la version VST de GRM Band Pass, utilisé en low pass de la même manière — cette fois, la pente est de 96dB / oct, donc le filtrage est différent. L’ordre de grandeur de modulation correspondant à l’effet recherché est sensiblement le même : rapport de fréquence crête à crête 1.2, ce qui correspond à un intervalle d’environ 3 demi-tons.

Comment expliquer une telle différence ?

Deux aspects distinguent cette expérience de la précédente : le son utilisé est beaucoup plus complexe, plus riche spectralement, et on s’occupe ici de filtrage, non plus de vitesse de playback. Un bref essai d’utilisation du son de l’expérience précédente dans le cas présent renvoie des valeurs du même ordre de grandeur que celui que l’on obtient en utilisant le son plus complexe : un rapport de fréquence d’environ 1.3. La différence serait donc dûe à la nature du traitement lui-même.

La situation est donc la suivante : on a utilisé la délinéarisation à petite échelle dans deux processus tout à fait différents, a ceci près que l’unité utilisée pour les mesures est la même dans les deux cas, ce qui nous permet de comparer objectivement les résultats. Et ces résultats sont extrêmement différents.

Cela voudrait dire qu’il n’y a pas de taux " typique " de délinéarisation, et que ceux ci changent du tout au tout suivant la nature de l’évolution à plus grande échelle que l’on délinéarise. Il conviendrait donc de rester prudent, et avant toute utilisation de ce procédé, de procéder à des tests permettant de déterminer l’ordre de grandeur convenable.    

6. Une expérience significative concernant la notion de formes

50	100	150	200

On peut constater une grande variété de formes, et une augmentation de la " pseudo fréquence " de ce système " pseudo périodique ". On peut modifier artificiellement la forme prise par la suite de ces valeurs en appliquant une fonction de transfert en sortie du module de calcul. Par exemple, on applique ici une fonction de transfert à X(t) pour la valeur 100 du Reynolds Number :

L’expérience :

Un son — un accord mineur tenu par un groupe de cordes, est traité à l’aide du plug-in VST Waves Ultrapitch — un pitch shifter avec reconnaissance des hauteurs, de la manière suivante : Un " repitchage " - pas une transposition — vers le haut autour de 6 demi-tons, et un vers le bas également autour de 6 demi-tons. Le tout est superposé au son original.  La sortie X(t) du système de Lorenz est dirigée vers le repitchage haut , et la sortie Z(t) vers le repitchage bas.

Cela donne deux évolutions pseudo périodiques synchronisées, centrés autour de +/- 6 demi tons. On produit donc de cette manière 6 fichiers son, en donnant successivement au nombre de Reynolds les valeurs 25, 50, 100, 150, 200 et 250. Puis on applique différentes courbes de transfert aux sorties X(t) et Z(t), en particulier la courbe suivante, qui provoque un doublement de la pseudo période :

  Résultats de l’expérience :

1. Même si, visuellement, la suite des valeurs semble pouvoir être, selon les principes du chapitre 1, perceptivement adaptée, une courbe de transfert judicieuse, choisie empiriquement, " optimise " très efficacement la richesse perceptive entendue.
2. La différence entendue lors de la modification de la courbe de transfert est plus importante que celle que l’on entend quand on modifie le nombre de Reynolds.
3. Si l’on n’utilise pas de courbes de transfert trop baroques, un résultat perceptivement adapté sans courbe de transfert le sera aussi avec — et inversement. Et ce, même lors de l’utilisation d’une courbe de transfert provoquant un doublement de la pseudo période.

Conclusions  :

A l’usage, on s’aperçoit rapidement que l’effet principal de l’optimisation empirique est de rendre les formes plus fortes. On peut en conclure que le système de Lorenz génère des formes un peu trop faibles pour être, au moins dans certains cas, perceptivement adaptées.

Le troisième point suggère une remarque intéressante : l’adaptation perceptive est résistante aux transformations simples. Ceci est finalement normal, si l’on songe que l’inadaptation perceptive l’est aussi : en effet, ce n’est pas en appliquant une courbe de transfert simple sur un sinus que l’on va créer un son intéressant et riche…

Une synthèse de ces deux remarques consisterait à dire que le rôle du système de Lorenz, ou de tout autre système susceptible d’être perceptivement adapté, est en quelque sorte d’apporter les éléments de cette adaptation, et pas une forme précise. La forme finale, elle peut être façonnée manuellement. Dans ce sens, le rôle de tels systèmes est d’être les garants de la richesse perceptive du résultat final.

Note : Au cours de cette expérience, on a essayé de désynchroniser X(t) et Z(t), dans le but de vérifier si cette synchronisation, naturellement apportée par le comportement du système de Lorenz, était importante. Et on s’est aperçu que sans synchronisation, les formes devenaient, d’un point de vue perceptif, beaucoup trop faibles. Cette synchronisation semble donc indispensable.

On peut par ailleurs en conclure qu’il est nécessaire d’appliquer la délinéarisation à petite échelle sur le paramètre rassemblé, et pas indépendamment sur chaque paramètre individuel ; donc, après le rassemblement des paramètres. Ainsi, on sera sûr d’obtenir des délinéarisations synchronisées, et donc des formes à petite échelle suffisamment fortes.

7. Délinéarisation à petite échelle et spatialisation liée au cube

L’idée est de faire vibrer plus ou moins rapidement l’axe de projection du son, ce pour tenter d’obtenir trois résultats distincts :

*** augmentation de la richesse perceptive, même si on ne sait pas encore quel aspect cette richesse peut prendre dans le cas présent.

*** en approche " réflexions ", une possible meilleure localisation de la source virtuelle du son — on s’appuie donc sur le principe que le cerveau localise mieux une source animée d’un léger mouvement - cf compte rendu Septembre 2000, bas de la page 16.

*** en approche " volume ", un élargissement de la zone de délocalisation, comme illustré sur le schéma suivant :

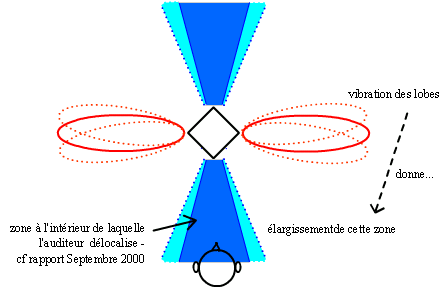
Rappelons les natures respectives des approches " réflexions " et " volume " :

1. la demi période de vibration
2. la vitesse de rotation lors du mouvement

Une demi-période d’une valeur élevée, associée à une vitesse de rotation lente, donnera une vibration ample et lente.

Au contraire, une demi-période faible et une vitesse rapide donnera une vibration courte et rapide. Une demi-période élevée associée à une vitesse de rotation donnera une vibration ample et rapide, etc…

La demi-période de rotation sera par la suite exprimée en millisecondes. La vitesse de rotation sera exprimée dans l’unité propre à la trackball. Equivalence : v = 1 correspond à 0.25 tour/seconde.

L’expérience : Cette composante à petite échelle est ajoutée successivement à trois composantes à grande échelle :

1. rayonnement bidirectionnel horizontal, transversal fixe 
2. rayonnement bidirectionnel horizontal en rotation (v = 1)
3. rayonnement hypercardioïde fixe, direction bas-arrière-gauche (pôles —0.82/0.54/-0.12)

Dans chacun des trois cas, on utilise le vibrateur avec les paramètres suivants :

1. rayonnement bidirectionnel horizontal, transversal fixe :

On écoute les résultats liés à l’application des valeurs de vibration appartenant aux trois groupes, dans l’optique d’y trouver l’effet " élargissement de la zone de délocalisation ". Le groupe donnant les meilleurs résultats est le groupe 2. En particulier, le couple de valeurs (54ms, v17) donne de bons résultats. Le groupe 3 donne lui aussi de bons résultats, mais au prix de l’apparition d’un " effet  Leslie " très marqué. Si l’on écoute les résultats dans l’optique d’y trouver l’effet " augmentation de la richesse perceptive ", ce que entend dans le groupe 3 est intéressant : cet " effet Leslie " est fort curieux, et ajoute à la confusion perceptive inhérente au rayonnement bidirectionnel fixe transversal.

 

2. rayonnement bidirectionnel horizontal avec rotation

Sans composante à petite échelle, on entend assez clairement, au moins dans le studio 4, une rotation du son autour du cube. Mais, quand on ajoute cette composante à petite échelle, les choses se passent moins bien : si les valeurs liées au groupe 1 n’apportent rien, les valeurs liées aux groupes 2 et 3 affaiblissent cette impression de rotation, sans rien apporter en retour. On peut en déduire que, dans la cas d’un rayonnement mobile en approche volume, l’ajout d’une composante à petite échelle est non seulement inutile mais aussi nuisible.

 

3. rayonnement hypercardioïde fixe

   Les résultats de cette expérience ont été écoutés dans le studio 4, endroit dans lequel l’approche réflexions fonctionne notoirement mal. Il est en effet presque impossible d’entendre une réflexion sur une des parois. Si l’on ajoute une composante à petite échelle, on peut entendre, notamment en utilisant le couple de valeurs (54ms, v17) du groupe 2, un léger progrès : une délocalisation fugitive pendant moins d’une seconde. On pourrait en conclure que l’ajout d’une composante à petite échelle serait susceptible, dans le cadre de l’approche réflexions, d’améliorer l’aspect " meilleure localisation de l’origine virtuelle du son ". Mais il faut impérativement écouter les résultats de cette expérience dans un autre endroit.  

Conclusions :

Dans le second cas, l’ajout d’une composante à petite échelle est non seulement inutile, mais encore nuisible. Dans le troisième, on ne peut se prononcer. Reste le premier cas. Dans ce cas-ci, le paramétrage du vibrateur le plus adapté, dans le cadre d’une optique " élargissement de la zone de délocalisation ", serait situé juste avant que l’effet Leslie commence à se faire entendre.

On peut se demander alors comment " repousser " cet effet Leslie le plus loin possible. Considérons alors la forme de la composante à petite échelle rajoutée : c’est une fonction en triangle. Reportons nous maintenant aux conclusions de l’expérience présentée lors du paragraphe 4 du présent chapitre, et aux principes exposés lors du chapitre 1 : les formes trop périodiques ne conviennent pas à une telle utilisation, car on les entend trop en tant que telles.

Il semble alors nécessaire d’utiliser, dans le cadre d’un tel processus, une composante à petite échelle dont la forme rappelle celle des formes 2 ou 3.

L’architecture de l’objet Max " trackball " nous interdit pour l’instant l’application de telles formes, mais le problème est en cours de résolution. Il devrait alors être possible d’élargir la zone de délocalisation de manière très significative.