Plaçons nous dans le cas de la réalisation d’une bande son à caractère exclusivement électroacoustique, destinée à une installation sonore. Une telle installation peut être supposée fonctionner pendant plusieurs heures d’affilée. Face à une telle contrainte, deux démarches distinctes peuvent être adoptées. Première démarche : on réalise une bande son d’une durée arbitraire, que l’on enregistre de façon conventionnelle sur bande ou sur disque dur, et cette bande son sera répétée ad libitum, en boucle, pendant la durée nécessaire. Seconde démarche : on prépare des échantillons, et on applique à ces échantillons des lois combinatoires. Le processus sera mis en marche pendant toute la durée de l’installation. Intéressons nous à la seconde démarche.
On imagine facilement qu’il y a là matière à de longues recherches. Le but de ce chapitre, qui n’a évidemment aucune valeur exhaustive, est d’exposer quelques principes pouvant servir de points de départ ou de repères dans le cadre d’une telle recherche. Et ce, toujours à la lumière des principes exposés lors du chapitre 1.
Reprenons le principe de ce que l’on appelle l’ " approche vectorielle " : point de départ, point d’arrivée, trajectoires, et appliquons-le à la présente problématique. Point de départ : un " état " de la musique Point d’arrivée : un autre " état " de la musique Trajectoire : transitions plus ou moins progressive de l’un à l’autre.
Définissons les termes en présence, en s’appuyant sur un exemple simple. Supposons pour cela quatre échantillons sonores joués l’un après l’autre, les transitions de l’un à l’autre se faisant à l’aide de crossfades. On décide de l’échantillon à jouer à un moment donné à l’aide d’un tirage, chaque échantillon étant associé à une probabilité d’apparition.
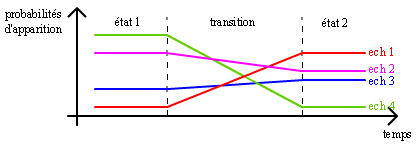
Ce qui nous donne : Point de départ : un ensemble de probabilités Point d’arrivée : un autre ensemble de probabilités Trajectoire : transition d’un groupe de probabilités à un autre Ce que l’on peut représenter comme suit :

…. les probabilités d’apparition étant bien entendu normées a posteriori pour que leur somme soit à tout instant égale à 1. Jusqu’ici, rien de bien extraordinaire, d’autant plus que les états de départ et d’arrivée sont définis par des principes simples, conventionnels et dépourvus de la personnalité qui en feraient des états intéressants d’un point de vue perceptif - ce dernier point étant abordé plus en détail dans les paragraphes 6 et suivants du présent chapitre.
Supposons alors les états de départ et d’arrivés perceptivement intéressants. Ils comportent, comme dans l’exemple précité, une " règle d’écriture " susceptible de donner à une juxtaposition d’échantillons une " personnalité dynamique " propre.
Ces états, appelés états extrêmes, sont définis
par un ensemble de paramètres — dans l’exemple ci dessus, il
y a donc quatre paramètres. Associons les valeurs des paramètres
de l’état 1 à la valeur 0 d’un paramètre global,
et les valeurs des paramètres de l’état 2 à la valeur
1 du même paramètre global. Cela nous donne, dans le cas de l’exemple
précédent :
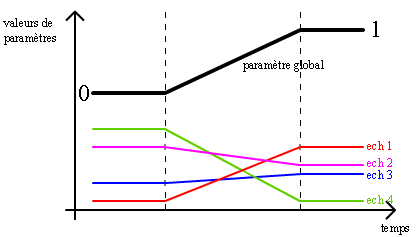
On a donc rassemblé les paramètres qui définissent les états, en un seul paramètre. Cette étape est essentielle, car, sous réserve d’un choix judicieux de 1. la forme des transitions entre les états et 2.des états eux même, elle permet de créer un paramètre d’évolution — un curseur — qui soit le reflet d’une réalité perceptive évidente, aussi évidente que peut l’être l’action sur un potentiomètre de volume. Dans toute la suite, on appellera ce type de paramètres " paramètre rassemblé ".
Cela nous permet donc, au moins en théorie, de gérer facilement et " automatiquement " l’évolution de phrases musicales, ce qui est un premier élément de réponse au problème posé. Quoi de plus simple en effet que la référence à une trajectoire unidimensionnelle, surtout quand la forme de cette trajectoire est très bien corrélée à une réalité perceptive évidente.
Il est évidemment essentiel, pour que l’installation sonore en question ne soit pas rapidement ennuyeuse, de ne pas se restreindre à deux états extrêmes et à leurs intermédiaires. On peut alors définir plusieurs états extrêmes suffisamment caractéristiques, et reprendre la même démarche. Cela nous conduit alors à des trajectoires que l’on pourrait qualifier de pluridimensionnelles, si, en pratique, on n’était pas souvent restreint à n’évoluer que sur une dimension à la fois . C’est à dire, souvent, on joue forcément sur l’évolution entre l’état 1 et l’état 2, ou entre l’état 1 et l’état 3. La notion de coordonnées au sens de l’algèbre linéaire n’a dans le cas présent pas tout le temps de sens, comme on peut le voir dans l’explication suivante.
1. Supposons que l’on décrète autant d’états extrêmes qu’il y a de paramètres individuels de définition d’états :
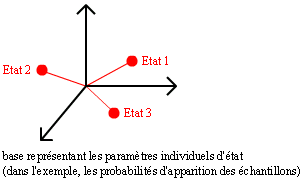
Comme on choisit les états extrêmes à partir de considérations purement perceptives, il n’y a pas de raison que les vecteurs définis par ces états soient indépendants. Avec 3 paramètres individuels, il y a effectivement de grandes chances qu’on les choisisse indépendants. Mais avec 10, c’est autre chose. Donc, comme les vecteurs en question ne sont pas indépendants, ils ne forment pas de base.
2. Si l’on décrète plus d’états extrêmes que de paramètres individuels, les vecteurs ainsi formés sont " encore moins " indépendants.
3. Si l’on décrète moins d’états extrêmes que de paramètres individuels, les vecteurs ainsi formés peuvent en effet être indépendants. C’est donc le seul cas où l’on peut théoriquement évoluer dans plusieurs directions à la fois.
Ce qui peut se résumer par :
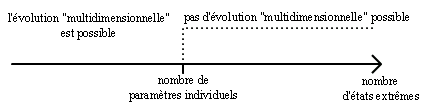
Ceci dit, en pratique, d’un point de vue perceptif, on observe
le phénomène suivant :
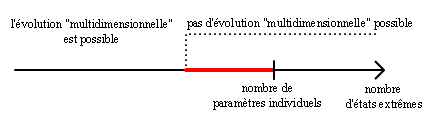
C’est à dire que l’évolution " multidimensionnelle " est déjà impossible bien avant que le nombre d’états extrêmes atteigne le nombre de paramètres individuels. En termes plus prosaïques, si l’on essaye de mélanger trois états extrêmes en même temps alors qu’il y a 5 paramètres individuels, on n’y comprend déjà plus rien.
Prenons maintenant un exemple réaliste : une installation sonore mettant en jeu notre traditionnel cube, et un patch Max qui gère à la fois la spatialisation, une reverb, un EQ, un compresseur, et l’agencement horizontal de 4 échantillons, par tirage comme dans l’exemple précité. Paramètres individuels : directivité, vitesse de rotation de l’axe de projection, caractéristiques de la reverb (nombreux paramètres, mais on peut se limiter à rapport dry / wet, TR moyen, et rapport TR HF/LF), caractéristiques de l’EQ (limitons nous à trois états fondamentaux), caractéristiques du compresseur (limitons nous au threshold) et enfin probabilités d’apparition des échantillons, au nombre de 4. Il y a plus d’une dizaine de paramètres individuels.
-- On décide 2 états extrêmes : ces états sont nettement différenciés, la transition est tout à fait compréhensible. On décide 3 états extrêmes : les états sont toujours très bien différenciés, et chaque transition reste compréhensible. On essaye une évolution mettant en jeu les trois états en même temps : déjà plus délicat, mais encore tout à fait compréhensible à l’audition.
-- On décide 4 états extrêmes : les états restent convenablement différenciés, les transitions restent convenables d’état à état. On essaye une évolution mettant en jeu les quatre états en même temps : il devient assez difficile de suivre les évolutions, alors qu’on sait précisément ce qu’on est en train de faire ; pour l’auditeur, le suivi est encore plus difficile…
--> On peut donc voir qu’en effet, toute évolution multidimensionnelle est impossible bien avant que le nombre d’états extrêmes atteigne le nombre de paramètres individuels. D’où vient cette différence flagrante avec ce qu’on aurait pu attendre ? Plusieurs possibilités :
Supposons que nous ayons mis en place un ensemble d’états extrêmes et de formes transitionnelles qui forment une base à un discours musical, au moins à une échelle donnée. Gardons alors ces même lois, mais changeons les échantillons sonores. Avec Max, cela revient à changer les fichiers son chargés dans les buffers, ce qui est simple.
On a donc : changement de la matière sonore, mais cohérence du discours musical. Si, au contraire, on garde les mêmes échantillons, mais on change les lois : cohérence de la matière sonore, mais changement de discours. Changeons échantillons et lois : cela change la nature de la musique du tout au tout, ce qui permet donc, tout en gardant les mêmes procédés, une évolution de la musique à plus grande échelle.
Autre chose : gardons les mêmes échantillons, et les mêmes lois d’évolution des paramètres globaux — ceux qui sont issus de la démarche de rassemblement des paramètres - cf paragraphe 2 . Mais : modifions les formes transitionnelles. On garde alors la même matière sonore, le même type de discours, mais le détail de ce discours est modifié : plus grande variété du discours.
Reprenons une nouvelle fois les principes évoqués au chapitre introductif, et cherchons à préciser, dans le cadre de l’approche vectorielle, les apports des différents éléments au niveau de la richesse perceptive à plusieurs échelles. C’est une réflexion qu’il faudrait évidemment mener au cas par cas, mais on peut tenter de dresser un portrait global de la situation telle qu’elle est généralement définie par cette approche vectorielle. Ceci nous permettra également de préciser cette notion de perception à plusieurs échelles.
Imaginons pour cela que les échantillons utilisés comme matériau sonore soient d’une durée de l’ordre de 5 à 10 secondes. Les lois gérant l’apparition de ces échantillons reposent sur les degrés de liberté suivant : tirages aléatoires pour la probabilité d’apparition de l’échantillon, et pour la durée de playback de cet échantillon. La longueur des crossfades est déduite de cette durée. Le patch Max servant à gérer notre installation met aussi en jeu une reverb. Cette installation comprend, pour la diffusion, un cube, et on joue sur la vitesse de rotation de l’axe de rayonnement.
Un état extrême est donc défini par un groupe de valeurs associés aux paramètres suivants : probabilités d’apparition des échantillons, vitesse de rotation de l’axe de rayonnement, réglages de la reverb. (note : le tableau suivant est évidemment non seulement perfectible, mais encore tout à fait approximatif et largement discutable — il semble néanmoins nécessaire : avant de perfectionner une approche, il convient déjà de lui donner une réalité )
| Ordre de grandeur | < 1sec. | 1 — 3 sec. | ~ 10 sec. | ~ 30 sec. | 1 min. + |
| Eléments concernés | nature de l’échantillon réglages de la reverb vitesse rotation axe | durée des crossfades (donc tirage durée échantillon) réglages de la reverb vitesse rotation axe formes transitionnelles | tirage durée échantillon probabilité apparition échantillon variations des paramètres rassemblés changement des formes transitionnelles | variations des paramètres rassemblés changements des lois (états extrêmes…) changement des échantillons | changements des lois (états extrêmes…) changement des échantillons |
Que nous montre ce tableau ?
Ceci dit, à propos de ce problème de la richesse à grande échelle :
Si l’on s’intéresse à la musique de la fin du XVIIIème — période classique, on peut remarquer que les lois qui régissent les évolutions à petite échelle, c’est à dire contrepoint et harmonie, sont bien plus rigoureuses que celles régissant les structures à plus grande échelle — forme sonate… et surtout ne sont pas les mêmes. On peut peut-être en déduire qu’il n’est pas judicieux de confier à une seule méthode la gestion de toutes les échelles de perception, et que les structures à plus grande échelle ressortent plus de l’arbitraire que de lois prédéfinies et appliquées.
Par ailleurs, les termes " évolution à petite échelle " et " structures à plus grande échelle " ne sont pas gratuits. Ils impliquent notamment qu’une approche basée sur des procédés d’évolution n’est pas adéquate pour la gestion du temps à grande échelle. Ce qui confirme l’hypothèse que l’approche vectorielle n’est pas applicable à ces échelles de temps.
Un des problèmes fondamentaux de l’approche vectorielle dans la perspective de la génération de matériau est bien évidemment la conception des " états extrêmes " au point de vue combinatoire. C’est à dire : à partir d’un nombre donné d’échantillons agencés, dans un premier temps, horizontalement, comment générer une matière vivante, ou, en utilisant une terminologie plus spécifique, perceptivement adaptée.
On ne va pas donner ici de méthode générale. On peut par contre se poser quelques questions et évoquer quelques principes de base concernant la mise en la mise en œuvre d’un tel processus. On peut distinguer au moins trois approches concernant la " juxtaposition horizontale " d’échantillons :
C’est à dire :
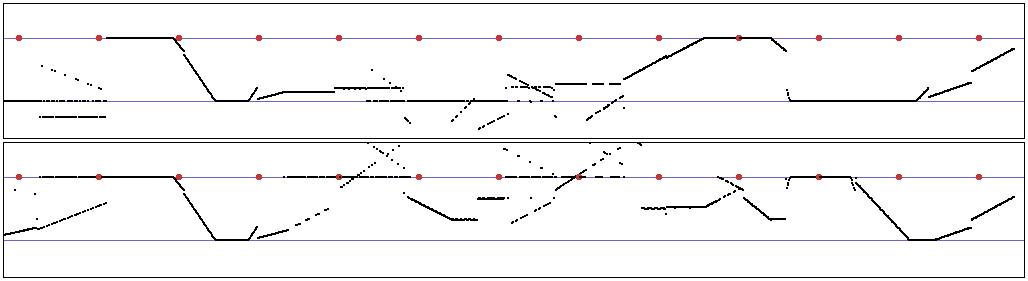
Si les deux premières approches sont assez semblables, et peuvent donner les mêmes résultats, la différence au niveau de la conception des processus est importante, et peut donner lieu à des développements assez différents. Ces trois approches ont en tous cas en commun le fait qu’elles mettent en scène une suite d’objets ou une suite de valeurs. Il n’est alors pas inutile de se demander d’un point de vue tout à fait intuitif à quoi peut ressembler une suite de valeurs, ou un système dynamique, associés à un comportement perceptivement intéressant — une application pratique des principes évoqués au chapitre 1. Voici par exemple quelques systèmes dynamiques représentés en fonction du temps — deux d’entre eux sont issus du " générateur de forme " évoqué au chapitre 2 :
 |
|
Exemple 1 (trois variables)
|
 |
|
Exemple 2 (une variable)
|
 |
|
Exemple 3 (deux variables)
|
 |
|
Exemple 4 (une variable)
|
On voit tout de suite que les systèmes donnés en exemple 2 et 4 ne pourrons pas être associés à des comportements perceptivement intéressants : l’un est trop périodique (ie présence d’information à une seule échelle de perception), et l’autre ne présente pas assez de formes fortes.
Par contre, les systèmes 1 et 3 possèdent certaines qualités : pas trop périodiques, autrement dit pas trop prévisibles, ce qui peut se traduire par " présence d’information à plusieurs échelles ", mais reconnaissables, c’est à dire à l’origine de formes suffisamment fortes. Revenons, à la lumière de ces constatations, aux trois approches précitées.
*Dans le cas de l’approche " paramétrique ", le problème est simple : la suite d’échantillon générée suivra la forme de la courbe représentative du système dynamique, comme on peut le voir dans le schéma suivant :
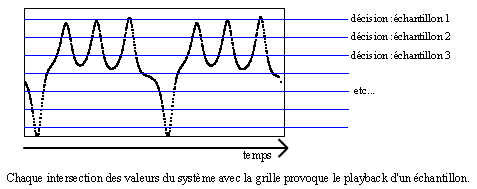
*Dans le cas de l’approche " récurrente ", plusieurs solutions possibles. On peut mettre au point un système dynamique discret — une suite récurrente Un = f(Un-1) se comportant d’une manière que l’on juge intéressante. On se retrouve alors dans le cas de l’approche paramétrique. On peut, à partir du groupe d’échantillons de départ, établir un ensemble de règles " décisionnelles " : une succession donnée interdite ou recommandée, des schémas de suite d’échantillons etc… ensemble que l’on exploitera ensuite à l’aide de tirages probabilistes ou autres.
Ou alors, on peut essayer d’exploiter les propriétés structurelles de ce type de processus. En effet, l’implémentation d’une récurrence est forcément associée à la présence d’une rétroaction, et une rétroaction, convenablement " pervertie ", engendre naturellement des perturbations, des " non-linéarités " qui peuvent donner existence à des comportements perceptivement adaptés. L’exemple 3 est une illustration du résultat d’une telle méthode, qu’on trouvera expliquée plus en détail au paragraphe suivant.
*Reste le problème de l’approche " non récurrente ", qui, par le simple fait qu’elle ne crée aucun lien entre les échantillons successifs, pose un problème évident de richesse dans le cadre d’une " écriture ". Rappelons que nous sommes dans le cas d’une écriture " horizontale ". Il est cependant possible de donner une forme très forte ou très particulière aux probabilités utilisées, de manière à provoquer des occurrences d’échantillons correspondant à une perception satisfaisante : des formes fortes, sans excès de périodicité. On peut aussi utiliser cette approche comme " bruiteur " d’une trajectoire simple : dans l’exemple du paragraphe 2 du présent chapitre, on est bien dans le cas d’une approche non récurrente. La compensation de la faiblesse des formes est donnée par la trajectoire manuelle ou arbitraire du paramètre rassemblé associé.
Au départ, on dispose de quatre échantillons, et on définit une méthode récurrente simple — une des plus simples qui puisse se trouver. Le principe au sens " décisionnel " est : ne pas répéter deux fois le même échantillon. Un tirage à probabilités uniformes décide lequel des trois autres échantillons va être joué la prochaine fois. La durée de playback de l’échantillon à venir est décidée à l’aide d’un tirage à probabilités uniformes sur l’intervalle ouvert à droite [durée fichier / 2 , durée fichier [ . Le résultat est le suivant :
|
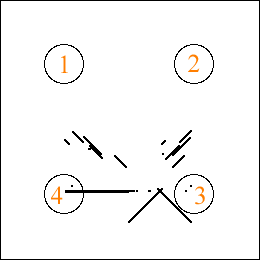
|
Chaque cercle représente un échantillon — on voit ici la représentation d’une décision de faire suivre l’échantillon 3 à l’échantillon 4. Ce comportement ne génère évidemment que des transitions simples, donc tout comportement sera représenté par des lignes reliant entre eux deux des cercles. |
|
Autre représentation - abscisse / ordonnée :
|
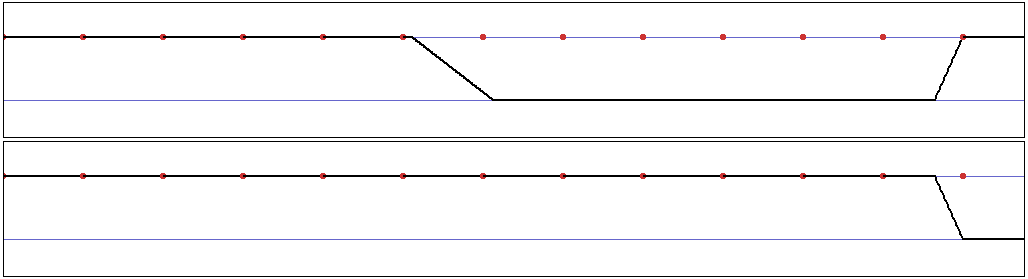 |
On voit ici, successivement, une transition entre l’échantillon 3 et l’échantillon 4, puis entre l’échantillon 4 et l’échantillon 2. Les points rouges représentent les secondes. Cette démarche renvoie un système perceptivement peu adapté, car manquant de formes à plusieurs échelles. On décide alors de l’améliorer en tirant parti de la rétroaction que contient le patch Max utilisé, en procédant de la manière suivante : Au moment où l’on commence à jouer un échantillon — échantillon n°1, on décide de la durée qu’il va s’écouler avant que le suivant — échantillon n°2 — soit joué. Au bout de ce temps là, un crossfade commence :
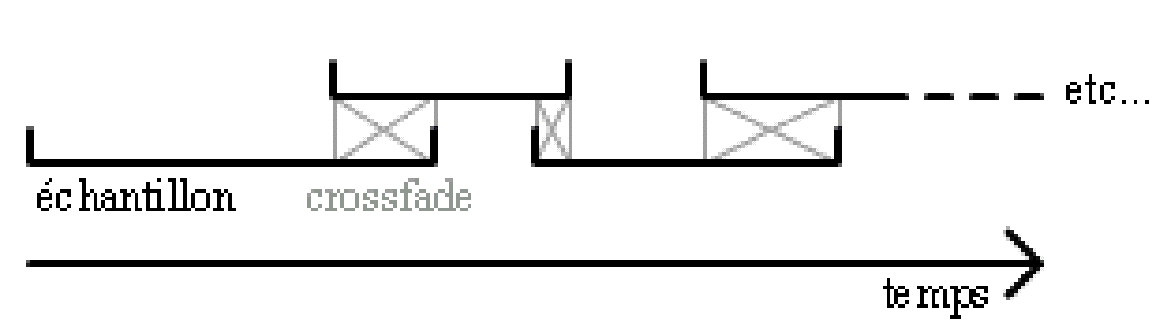
Pour que tout se passe bien, il faut évidemment que la décision de commencer l’échantillon n°3 intervienne après que le crossfade liant le n°1 avec le n°2 soit terminé. Que se passe-t-il le cas échéant ? En première approximation, une superposition de quatre sons. Mais ceci n’est pas possible étant donnée le procédé utilisé : puisque l’objet de la décision est une trajectoire et non le déclenchement d’un échantillon, le résultat n’est pas une simple polyphonie. Mais plutôt, on prend deux chemins en même temps. Au niveau du résultat auditif, cela se traduit par une succession intermittente très rapide des deux chemins, donc des deux crossfades, ce qui donne une forte impression d’instabilité.
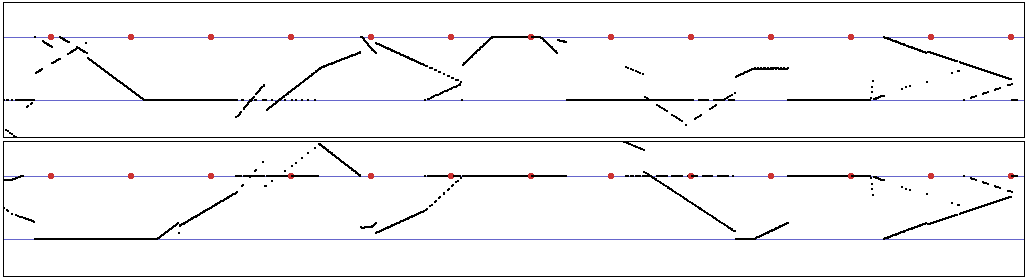
Mais rappelons qu’on est dans un schéma récurrent avec rétroaction, qui se base sur l’état actuel pour déterminer l’état suivant. Dans le cas présent, l’état actuel est double : il y a deux états, et donc deux décisions, dans le laps de temps pendant lequel il ne devrait y avoir qu’un état et donc qu’une seule décision. Si les deux décisions convergent, ou que le laps de temps avant qu’une troisième décision soit prise est suffisamment grand, cet état double se réduit à un état simple, " normal ", et l’instabilité se résorbe. Sinon, deux décisions contradictoires sont prises, et l’instabilité continue. Il est aussi possible qu’un troisième, ou quatrième état apparaisse, et l’instabilité augmente : des décisions contradictoires sont prises à intervalles rapprochés. Visuellement, cela se traduit par les représentations suivantes :
 |
|
et...
|
 |
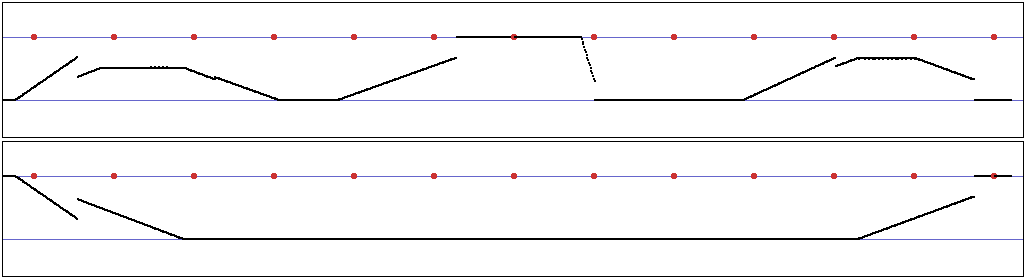
Ce " degré de désordre " est paramétrable : En effet, puisque l’instabilité est provoquée le chevauchement de deux crossfades, on allonge alors la longueur normale du crossfade par un coefficient donné, au delà même de la fin du son " sortant ". Ce coefficient est alors le paramètre de comportement du système. Par exemple, voici des représentations de ce comportement pour différentes valeurs de ce paramètre :
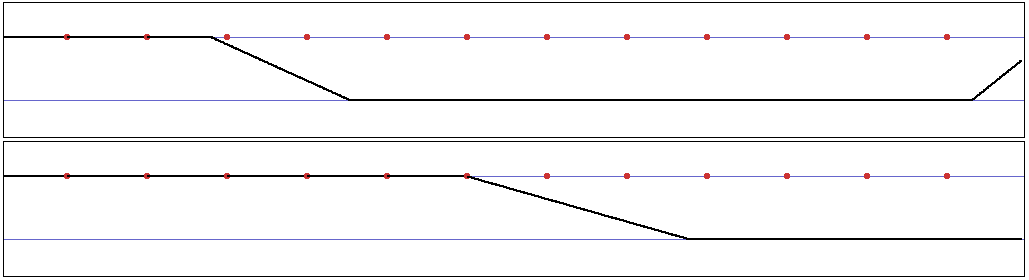 |
|
p = 1 (fonctionnement normal)
|
 |
|
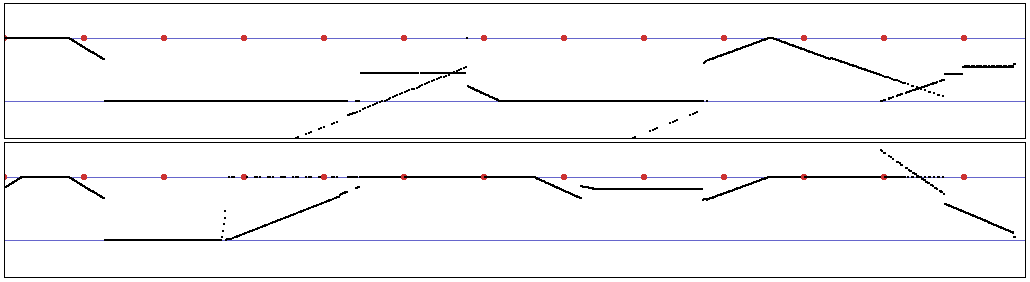
p = 1. 5 ( premières perturbations )
|
 |
|
p = 3 (intermittence états stables
/ perturbations)
|
 |
|
p = 5 (encore quelques plages de stabilités)
|
 |
|
p = 8 (situation constamment perturbée)
|