Le but de ce chapitre est principalement de donner une définition à certains termes utilisés tout au long de l’exposé, ainsi que d’apporter des justifications théoriques à l’utilisation des notions sous-jacentes aux termes en question.
Ces justifications théoriques sont à considérer avec une extrême prudence.
En effet, la plupart des raisonnements exposés sont facilement récusables, et s’appuient sur des notions relativement mal définies — quoi de moins étonnant dans la mesure où l’on cherche ici à " objectiver la subjectivité ".
Il n’est donc pas utile de chercher dans ce chapitre de vérités
solides au sens scientifique. Par contre, on pourra y trouver différents
points de vue d’un ensemble de notions non seulement cohérentes,
mais encore très utiles aux problèmes abordés lors des
chapitres suivants.
Point de vue défendu par le mathématicien Benoit Mandelbrot, au cours d’un séminaire " musique et mathématique ", Lyon 1996 — résumé :
Question : pourquoi trouve-t-on généralement la cathédrale de Notre Dame de Paris intéressante à regarder, alors qu’on ne peut pas en dire autant d’un immeuble typique des années 70 ?
Réponse : parce que, dans le premier cas, il est possible
de trouver beaucoup d’information quelque soit l’échelle d’observation,
et pas dans le second.
Il est vrai que si l’on regarde la cathédrale ND à 100m de distance, on va voir l’entrée, les tours, la rosace… à 10m, on peut observer des gargouilles, l’architecture générale de la rosace, les sculptures de chaque côté de la porte… à 1m, on voit à quoi ressemblent les gargouilles, le détail de la rosace, la forme de la robe d’un personnage présent parmi les sculptures qu’il y a de chaque côté de la porte…
On peut aussi noter que quelque soit la distance, ce qu’on voit n’est pas immédiatement compréhensible, schématisable, du fait de l’irrégularité des formes. Donc : on peut observer des formes non schématisables immédiatement, et ce à toutes les échelles d’observation, les formes étant propres à chaque échelle d’observation.
On regarde maintenant notre immeuble des années 70. A 100m de distance, on voit un parallélépipède rectangle, nanti de plusieurs rangées de fenêtres régulièrement disposées…. à 10m, on s’aperçoit que ces fenêtres sont finalement séparées en deux au milieu, ce qui est une information très pauvre…. à 1m, on n’a aucune information nouvelle concernant les fenêtres en question….
Donc : on observe des formes schématisables immédiatement, qui varient peu suivant l’échelle d’observation.
Une opposition radicale :
* L’homme a " inventé " le carré, le cercle, la droite, ce qu’on appelle la régularité… ces formes lui paraissent naturelles. Il suffit de regarder la forme de la feuille sur laquelle est écrit ce texte, ou de regarder par la fenêtre — elle même tendant à être rectangulaire — pour s’en rendre compte.
* La " nature " a " inventé " l’irrégularité, et ces formes " lui " paraissent naturelles. Par contre, pas du tout évidentes pour notre esprit : il est impossible pour un être humain normalement constitué de mémoriser la forme d’un arbre, pas plus que la texture à la surface d’un océan, ou que la forme d’une montagne. Et, si l’on en croit ce qui est dit dans le paragraphe précédent, quand on crée des objets basés géométriquement sur des formes régulières " inventées " par l’homme, ces objets ne sont pas intéressant d’un point de vue perceptif.
On peut donc, en suivant ce raisonnement, affirmer que :
Il est alors possible de se poser la question suivante : pour créer des objets perceptivement intéressants, sur quel type de forme doit-on se baser ? Le premier paragraphe comporte des éléments de réponse à cette question. Essayons de trouver d’autres éléments.
Dans les perspectives évoquées lors des deux premiers paragraphes, considérons maintenant quelques objets géométriques.
Un carré, un cube, un cercle… : des informations à une seule échelle de perception - à cette échelle, régularité, ou pauvreté suivant l’interprétation — adéquation à l’esprit — inadéquation à la perception.
Une portion de plan ou d’espace remplie par un nombre fini de points disposés aléatoirement suivant une loi de probabilité uniforme : des informations irrégulières à plusieurs échelles de perception, mais inadéquation à la perception.
Nous voici alors face à une contradiction
apparente : un objet irrégulier à plusieurs échelles
de perception, mais peu intéressant à regarder.
Il
est donc nécessaire de compléter le point de vue abordé
au premier paragraphe par une nouvelle notion : celle d’ordre/désordre
apparent à une échelle donnée.
Dans le cas présent — la portion de plan remplie par un nombre fini de points disposés aléatoirement suivant une loi de probabilité uniforme - les informations certes irrégulières que l’on peut trouver à plusieurs échelles d’observation ne sont pas perceptivement intéressantes, car pas assez ordonnées.
Il y aurait plusieurs moyens formels pour quantifier cette notion d’ ordre/désordre, mais ce n’est pas là notre propos, qui, rappelons-le, est d’évoquer d’un point de vue qualitatif différentes notions se rapportant à la perception en général.
Il serait donc nécessaire, pour qu’un objet soit adapté à la perception, qu’il comporte, au moins à une échelle d’observation, des formes ni trop désordonnées, ni trop ordonnées. Ce qui pourrait se reformuler ainsi : des formes non immédiatement compréhensibles, mais compréhensibles tout de même au bout d’un certain temps.
** Considérons alors trois objets, que
l’on regarde d’une seule et même perspective, d’une
même distance.
Le carré est perceptivement inadapté :
trop ordonné, immédiatement compréhensible
L’arbre est perceptivement adapté : compréhensible
au bout d’un certain temps
La forme uniformément
aléatoire est perceptivement inadaptée : une forme incompréhensible,
que l’on peut très difficilement décrire.
( rappelons que l’on se limite à une seule échelle d’observation )
** Trois autres objets, que l’on observe pour ses propriétés à l’échelle d’un laps de temps donné :
Tout le problème est donc de trouver des objets " centraux " au sens de cette perspective ordre / désordre à une échelle donnée.
Rappelons la question posée au paragraphe 2., qui est une autre formulation
de ce problème, d’un point de vue différent : pour être
perceptivement intéressant, sur quel type de formes doit-on se baser ?
Ces termes, empruntés à Michel Chion, sont une formulation différente
d’une notion immédiatement dérivée de la notion d’ordre/désordre
à une échelle donnée. Une forme forte est, à une
échelle donnée, une forme reconnaissable, identifiable.
Un carré est une forme très forte. Une répartition aléatoire uniforme, est, de loin, une forme très faible.
La différence essentielle entre forme forte/faible et ordre/désordre est que la seconde notion est quantifiable et généralement définie par des principes mathématiques. La notion de forme forte/faible, au contraire, est une notion purement perceptive, et, pour cette raison, tout à fait adaptée à notre propos.
C’est pourquoi, dans la suite de l’exposé, on utilisera ce vocabulaire de forme forte/faible en lieu et place de celui d’ordre/désordre.
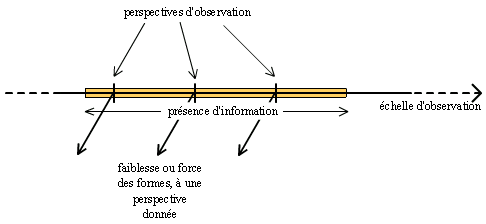
On a donc cherché à définir quelques notions qualitatives qui pourraient constituer un cadre propice à l’évaluation de l’adaptation à la perception d’objets quelconques. Ces quelques notions peuvent être représentées sur un graphe à deux dimensions :

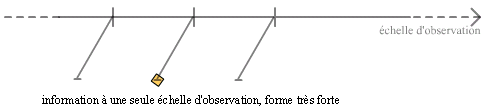
Voici comment on pourrait placer, sur un tel graphe, un carré :
Un arbre :

Une répartition aléatoire uniforme de points occupant une surface rectangulaire :
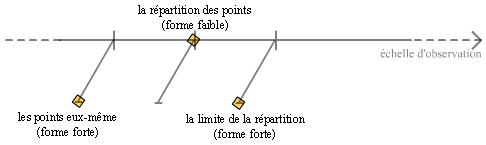
Sur ces graphes, pour des raisons pratiques évidentes, on n’a représenté qu’un nombre arbitraire de perspectives d’observation. Il convient cependant de préciser que la répartition des perspectives d’observation est forcément une notion arbitraire, à part dans certains cas très particuliers. Cependant, il est souvent possible d’observer un ordre de grandeur pour lequel la densité d’informations est particulièrement grande, ou particulièrement significative.
On voit donc que la notion d’adaptation d’une forme à la perception, ou " adaptation perceptive ", est une notion qui, si elle n’est pas quantifiable, peut être rapporté à un ensemble de notions qualitatives compréhensibles et cohérentes.
C’est cet ensemble de notions que l’on va très souvent utiliser dans la suite de l’exposé, chaque fois que l’on aura, entre autres, à enrichir perceptivement un son, ou à juger des qualités potentielles du comportement fonction du temps d’un système dynamique.