III.1) Commentaires informels des sujets

III.1.1) La difficulté des expériences

Après chaque expérience, les impressions des sujets étaient consignées. Les expériences ont été jugées dans l'ensemble assez faciles. Les sujets ont jugé l'expérience 1 plus facile que l'expérience 2, et l'expérience 2 plus facile que la 3. L'habitude et la fatigue ont semblé prendre part dans l'appréciation des expériences, mais les sujets expliquaient en partie la difficulté de l'expérience 3 par un rapprochement des sons ( "les sons se ressemblent plus, j'ai plus de mal à faire la différence").
Les expériences 1-2 et 1-3, par leur grand nombre de stimulis, ont été jugées souvent plus fatigantes, que les expériences 1, 2, et 3. Par contre l'expérience 1-2 a souvent été jugée plus facile que les expériences 1,2 et 3. Cette appréciation, à priori étonnante, pourrait être expliquée par l'expérience acquise par les sujets. Mais les sujets ont également jugé l'expérience 1-3 plus dure que toutes les autres.

III.1.2) Les stratégies

Les sujets avançaient en premier lieu des critères temporels. Certains citaient explicitement l'attaque, d'autres la décroissance temporelle. Les adjectifs comme "sec-résonnant", "vibrant-non vibrant", souvent employés peuvent également être ramenés aux qualités temporelles du son. Les instruments impulsifs et les instruments entretenus étaient donc les premiers à être discriminés.
Puis les sujets exprimaient des adjectifs comme "ouvert-fermé", " sourd-clair", "grave-aigue", "dur-mou". Ces adjectifs font penser à un aspect spectral, qui devrait être représenté par le centre de gravité spectral. "Nasal", "rond", "doux-amer" font également penser à des aspects spectrals. Ils devraient être représentatifs de la régularité spectrale.
Finalement des adjectifs comme "soufflé", "bruité", "vent" sont suggestifs du bruit produit par les instruments.

III.1.3) La reconnaissance des instruments.

Les instruments ont été reconnus de façon très diverse suivant la compétence musicale, mais plusieurs caractéristiques sont communes à presque tous les sujets :
- Les sons sxA et sxB n'ont pas été reconnus comme sons de synthèse issus du saxophone, mais plutôt comme des sons un peu bizarres proches du hautbois ou de la clarinette. Il est intéressant de remarquer que le saxophone, qui est un instrument populaire, perd toute identité lorsque la partie bruitée de son signal lui est enlevée (rappelons que le sxA1 est un son de saxophone naturel sans sa partie bruitée). Il est par contre moins étonnant que le sxB, possédant une enveloppe spectrale étirée, soit assimilé à un hautbois, qui est connu pour être un instrument "aigre et aigu".
Ce tableau montre le nombre de personne qui a reconnu les instruments sxA et sxB comme étant des instruments de synthèse issus du saxophone, ainsi que le pourcentage de personne l'ayant confondu avec l'instrument suivant.

- Le violon1, le violon2, la contrebasse 1 et 2, ont été souvent confondus avec un violoncelle ou un alto. Le Si2 et le Do#3 étant haut pour la tessiture conventionnelle de la contrebasse, et bas pour celle du violon. Les sujets leur ont préféré la contrebasse et l'alto, ayant des tessitures où ces deux notes sont plus fréquentes. Le violon3 a été par contre bien reconnu. La contrebasse3 quant à elle a été confondue avec le violon.

- La guitare et la harpe ont souvent été confondues. Le mode de jeu d'une harpe, souvent fait de nombreux arpéges, est très différent de celui de la guitare, fréquemment utilisée en musique flamenco ou en folk. Il est donc peu fréquent de confondre les deux instruments. Mais lorsque les deux instruments ne jouent qu'une seule note, la difficulté est autre.Leurs enveloppes temporelles étant proches, seule une bonne discrimination de leur contenu spectral peut permettre de les dissocier.
reconnu confondu avec

- Le violon pizzicato a été dans l'ensemble bien reconnu, malgré le fait qu'il a été souvent confondu avec l'alto ou le violoncelle.
reconnu confondu avec

- La trompette, et le cor ont été généralement bien reconnus. La faible évolution de leurs timbres a dû influencer cette bonne reconnaissance.

- La clarinette a souvent été bien reconnue. Contrairement à la trompette et au cor, le timbre de cet instrument varie beaucoup avec la fréquence fondamentale.
reconnu confondu avec

III.2) Analyses des résultats bruts

Les résultats de chaque expérience ont été automatiquement enregistrés à l'intérieur d'un fichier texte. Chaque fichier était nommé d'après le numéro de l'expérience, suivie du nom du sujet, et contenait pour chaque paire la définition des stimulis et la réponse des sujets sur une échelle allant de 0 (semblable) à 1 (différent). Pour les expériences 1-2 e 1-3 l'ordre grave-aigu était indiqué par un booléen.

Exemple de fichier enregistré sous le nom de exp1.dupond
(le 0 représentant le sxA, 1:bas,2:clt,3:cor,4:flt,5:gui,6:hrp,7:htb,8:sxB,9:trp,10:vln,11:vlp)
starting at: ---------------- Fri May 12 09:16:24 2000
9 10 0.260163
5 2 0.70935
2 6 0.51626
9 5 0.849594
5 6 0.268293
7 7 0.
1 11 0.951219
1 3 0.386179
4 9 0.264228

...III.2.1) Expériences 1,2 ,3

Les résultats individuels ont été extraits des fichiers de résultats et mis sous forme de trois matrices 12*12. Ces matrices sont triangulaires, c'est-à-dire que la moitié triangulaire haute droite est nulle, seule la deuxième moitié contient les informations de l'expérience.
La diagonale du fou
La diagonale, quant à elle, contient le 'garde fou' de notre expérience. En effet, c'est à cet endroit qu'est inscrit le résultat de l'évaluation des paires contenant le même son (vln1 et vln1 par exemple). On peut donc s'y assurer que tous les sujets ont accompli la tâche correctement. Il se trouve que même si cette diagonale n'était pas toujours équivalente à zéro, elle ne dépassait jamais un très faible niveau, inférieur à 0,13 . Aucun sujet n'a donc été écarté.

Les résultats moyennés

Pour chaque expérience, les matrices des sujets ont été moyennées. Elles sont représentées dans les figures suivantes, la couleur représentant l'échelle de différence perçue.

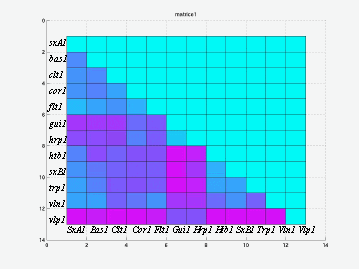
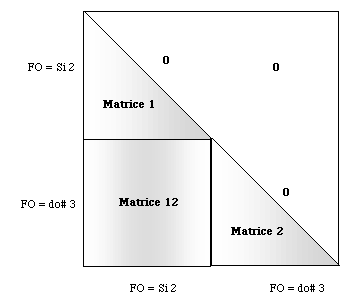
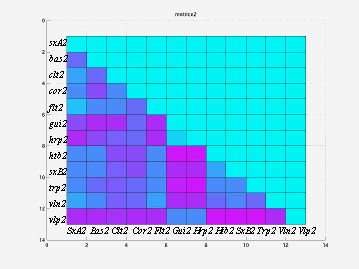
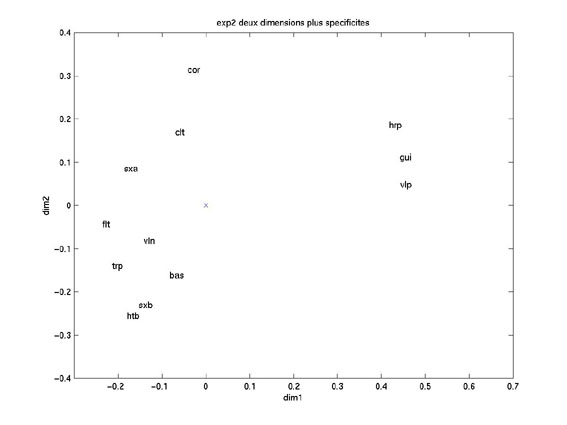
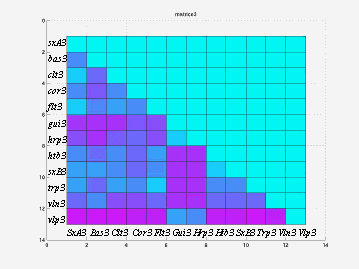
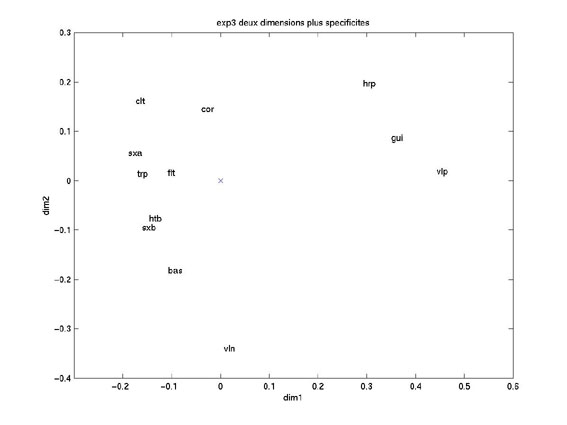
figure 4:matrice de l'expérience 1	figure 5:matrice de l'expérience 2	figure 6:matrice de l'expérience 3

Nous pouvons faire les remarques suivantes sur les trois matrices:
- Peu de différences sont visibles . Cela nous indique que les trois expériences donnent des résultats cohérents entre elles, que les sujets ont jugé les différences entre les timbres d'une façon assez similaire aux trois fréquences fondamentales.
- Le violon pizzicato, ainsi que la harpe et la guitare, ressortent comme étant nettement différents des autres sons. Cela suggère une ségrégation nette entre instruments impulsifs et entretenus dans les trois expériences.
- La guitare et la harpe sont proches dans les trois expériences. Il en va de même pour le sxB et le hautbois. Nous avons vu un peu plus haut que ces deux paires d'instruments étaient souvent confondues lors de la tâche de reconnaissance.
- La guitare et la harpe se rapprochent progressivement du violon pizzicato. Ceci appuie l'hypothèse que lorsque la fréquence augmente, le contenu spectral perçu s'appauvrissant, les sujets augmentent le poids des aspects temporels au détriment des aspects spectraux. La guitare et le violon pizzicato se rapprochent donc, malgré une différence spectrale, car leurs aspects temporels sont proches.

III.3) Analyses des expériences 1-2,1-3

Comme pour les expériences 1,2 et 3, les résultats moyennés ont été représentés à l'aide d'une matrice colorée. Les matrices sont maintenant pleines, car elles représentent les résultats des 144 paires présentées, chaque son à une hauteur étant comparé à chaque son à l’autre hauteur

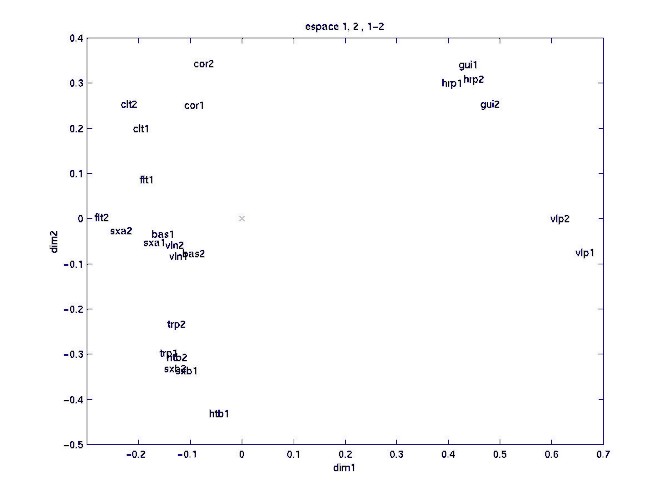
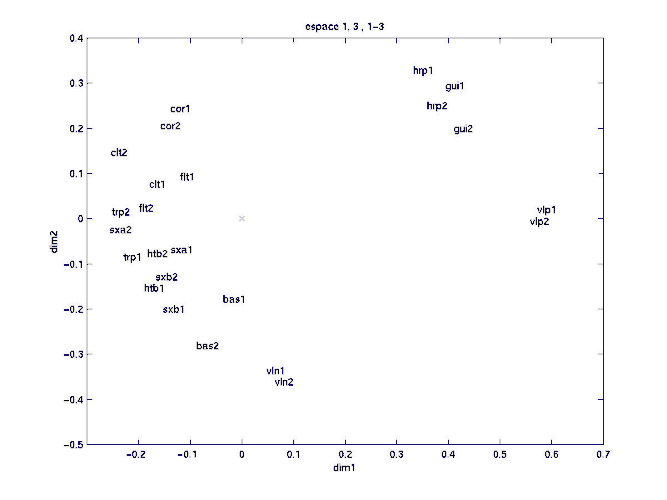
figure 7:matrice de l'expérience 2	figure 8:matrice de l'expérience 1-3

III.3.1) La symétrie des matrices

La première constatation visuelle, que nous pouvons remarquer, est la grande symétrie de ces matrices. Afin de l'apprécier d'une manière plus mathématique, nous avons décomposé chaque matrice en une partie symétrique et une partie antisymétrique, à l'aide à la formule suivante :

A_symétrique = (A+A')/2
A_antisymétrique = (A-A')/2

Les coefficients de corrélation entre les matrices 1-2 et 1-3, et leur parties symétrique et antisymétrique confirment que ces matrices sont essentiellement symétriques.

La symétrie des matrices 1-2 et 1-3 nous permet de faire la moyenne des parties supérieures et inférieures à la diagonale afin d'obtenir une matrice triangulaire comparable aux matrices 1, 2, 3. Dans la suite nous désignerons par matrices 1-2 et 1-3 ces matrices moyénées.
Les diagonales représentent la dissemblance entre deux notes du même instrument mais de hauteur différente (vln1 avec vln2 par exemple). On observe ces valeurs sont faibles.
Les instruments impulsifs ressortent de nouveau par rapport aux autres. Cette particularité est encore plus nette pour l'expérience 1-3, appuyant l'hypothèse de l'accroissement du poids des aspects temporels lors de cette expérience.

III.3.2) Les corrélations entre les matrices

Le tableau suivant indique les coefficients de corrélation entre les matrices 1, 2, 3 et les matrices moyénées 1-2 et 1-3. Les valeurs de ces coefficents sont très élevées, indiquant que les jugements de dissemblance sont très semblables lorsqu'ils sont effectués entre sons de F0 identique, ou entre sons de F0 différente.

III.4) Analyse multidimensionnelles

III.4.1) EXSCAL

Afin de représenter les résultats dans un espace de timbre, le programme EXSCAL a été utilisé. Ce programme a été conçu par Douglas Carroll et Suzanne Winsberg (McAdams, Winsberg et al. 95). Les paramètres du programme sont le nombre de classes de sujets à estimer, le nombre minimum et maximum de dimensions, et un paramètre qui indique si les sons comportent des spécificités ou non. En sortie, le programme indique la position de chaque instrument à l'intérieur des différents espaces, une mesure (BIC) qui indique la qualité du modèle (cette mesure tient compte de la qualité de l'approximation et du nombre de paramètres) puis, si on l'a demandé, les valeurs des spécificités de chaque instrument. Ce programme considère que tous les sujets répondent en fonction des mêmes dimensions perceptives, mais que chaque personne attribue un poids différent à chaque dimension. Il minimise la différence entre les dissemblances mesurées et les distances du modèle spatial. Ces distances sont calculés à partir de cette équation :

III.4.2) Evaluation de la qualité des modèles selon le critère BIC

Nous avons analysé les données des expériences 1, 2 e 3, ainsi que celles des expériences 1-2 et 1-3 (moyenne des triangles supérieurs et inférieurs). Les paramètres du programme d'analyse étaient:- Nombre de classes = 1 (le nombre de sujets était insuffisant pour pouvoir les diviser en plusieurs classes).
- Nombre de dimensions minimum = 1.
- Nombre de dimensions maximum =6. Le petit nombre d'instruments, 12, ne nous permet pas en principe de représenter les données dans un espace à plus de quatre dimensions, mais nous avons choisi six dimensions, afin de ne rien négliger.
- Spécificité = non pour une première série d'analyses, oui pour une deuxième.

III.4.3) Choix du modèle

Ci-dessous, le tableau des estimations BIC pour les 5 expériences et le 12 jeux de paramètres. Plus le BIC est faible, meilleur est la qualité du modèle.

Les résultats en gras représentent les meilleures estimations: espace à 3 et 4 dimensions sans spécificités, ou espace à 2 dimensions avec spécificités. Quatre dimensions ne pouvant donner de représentations fiables pour un espace ne contenant que 12 instruments (Donnadieu 1995), je me suis contenté d'analyser l' espace à 3 dimensions sans spécificités et l'espace à 2 dimensions avec spécificités. Les comparaisons de ces dimensions avec les dimensions physiques (décrites plus loin) ont donné de bien meilleures corrélations avec la solution à deux dimensions avec spécificités. Pour cette raison, et pour simplifier la discussion des résultats, je ne présenterai en détail que les résultats de l'analyse en deux dimensions avec spécificité. Les résultatsde la solution à trois dimensions sont présentés dans l'annexe.

III.4.4) L'espace à deux dimensions avec spécificités

Afin de pouvoir comparer les espaces des expériences 1, 2 et 3, il a fallu tous les orienter selon un même référentiel. Pour cela nous avons recalculé les espaces de l'expérience 1 avec les paramètres suivants :
- Nombre de classes = 20 (une classe par sujet).
- Nombre de dimensions minimum = 2.
- Nombre de dimensions maximal =2.
- Spécificités = oui.

Le programme a estimé un espace à deux dimension avec spécificités, ou chaque sujet est considéré comme unique composant de la classe qu'il représente. Cela nous permet d'obtenir un espace perceptif où le poids de chaque sujet sur chaque dimension, Wnr, et spécificité, Vn, était considéré séparément. Cet espace nous a donc servi de référentiel. A l'aide du programme "PROCRUST" les espaces à 2 dimensions, une classe, avec spécificités, sont réorientés selon le même axe que l'espace à 2 dimensions, 20 classes. Ainsi nous pourrons essayer de suivre les évolutions des timbres au cours des trois expériences. Les figures suivantes montrent les espaces réorientés pour les expériences 1, 2 et 3.

Nous observons que les trois instruments impulsifs sont distants par rapport aux neuf autres instruments. Il semble même y avoir une discontinuité sur la dimension 1: aucun instrument ne se situe sur cet axe entre la harpe, placée autour de 0,4 et le cor, placé autour de 0.

III.4.5) Corrélation entre les expériences

Afin de mieux estimer les similitudes entre les espaces, des coefficients de corrélation ont été calculés. D'abord entre les espaces réorientés :

Puis dimension-par-dimension:

Dimension 1:

Dimension 2:

Les corrélations entre les espaces sont bonnes, entre 0,78 et 0,89, ce qui indique que les espaces n’évoluent pas de façon aléatoire d'une expérience à l'autre. Les corrélations de la première dimension des trois expériences est très bonne. Celles de la deuxième sont inférieures à celles de la première, en particulier entre expériences 1 et 3, mais restent bonnes. Ces corrélations indiquent que la position de chaque instrument par rapport aux autres reste la même dans les différents espaces. En revanche elles ne permettent pas de comparer la position d'un instrument dans un espace avec celle du même instrument dans un autre espace. L'analyse des matrices composites présentée plus loin tentera de répondre à cette question.

III.5) Corrélations avec les dimensions physiques

Je me suis basé sur 37 paramètres physiques qui décrivent divers aspects du signal, décrits par Peeters (2000), qui lui-même s'est basé sur les travaux de Krimphoff (1994) et de Misdariis et al. (1998). Des algorithmes ont été implémentés sur MATLAB, afin d'extraire ces paramètres des 36 stimulis.

La réponse en fréquence du casque utilisée a été évaluée et les stimili filtrés avec cette réponse. Les stimuli filtrés approximaient mieux les sons entendus par les sujets. Les 37 paramètres extraits des 36 stimuli ont été corrélés avec les dimensions perceptives issues de l'analyse des expériences.

La liste complète des corrélations est donnée dans l'annexe.

III.5.1) La première dimension

Cette dimension est bien corrélée avec les paramètres physiques liés à des aspects temporels.

-Où "ltm" est une façon d'estimer le logarithme du temps d'attaque.

ltm = log₁₀ ( t_max - t_seuil )

Analyse des matrices composites (1,2,1-2) et (1,3,1-3)Les analyses précédentes renseignent sur les positions relatives des instruments dans chaque espace, la stabilité de ces positions relatives d'un espace à l'autre, et la stabilité des corrélations avec les paramètres physiques. Elles ne permettent pas de dire si le timbre change d'un F0 à l'autre. L'analyse de cette section tente de répondre à cette question.

Les matrices de dissemblance des expériences 1 et 2 sont triangulaires et la matrice (brute) de l'expérience 1-2 est carrée. En les assemblant on peut obtenir une matrice triangulaire de dimension 24X24, dans laquelle chacune des conditions (instrument, F0) est associée avec chacune des autres conditions (instrument, F0). Formellement, cette matrice ressemble aux matrices triangulaires des différentes expériences, et on peut lui appliquer le programme EXSCAL pour obtenir un espace composite dans laquelle figurent les 24 stimulis (instrument, F0). Cela permet (en comparant pour chaque instrument les positions aux deux F0) d'évaluer l'effet de la F0 sur le timbre (cette analyse est cependant à manier avec précaution dans la mesure où les jugements de dissemblance n'ont pas été faits parmi l'ensemble complet des 24 paires). La même opération peut être faite avec les matrices 1, 3 et 1-3.

figure 12 : schéma de la grande matrice

figure 13 : grand espace 1,2 et 1-2

Quel que soit l'instrument, la position reste sensiblement la même pour les deux F0. La dimension 1 reste particulièrement stable.

Nous avons utilisé le même procédé avec les matrices 1, 3 et 1-3.

Encore une fois, quel que soit l'instrument, la position reste sensiblement la même pour les deux F0, ce qui suggère une certaine invariance du timbre en fonction de F0. Il faut encore une fois souligner les limites de cette interprétation. Nous interprétons comme résultant d'une expérience unique de jugement de dissemblance entre 24 stimuli, des données provenant de trois expériences distinctes de dissemblance entre des jeux de stimuli réduits. L'expérience que nous simulons (celle à 24 stimuli) n'est pas directement réalisable du fait de la taille du jeu de stimuli, et du fait que, contrairement à nos expériences, les comparaisons ne se font pas à F0 ou différence de F0 constante. L'ensemble de stimuli comprendrait des paires à même F0 et à F0 différente, et les jugements risquent donc d'être dominés par la dimension "hauteur", comme dans les études précédentes. Cette question pourrait faire l'objet d'expériences futures.

Deux aspects remarquables sont d'emblée évidents dans les matrices de ressemblance-dissemblance, avant même l'analyse multidimensionnelle. Le premier est la très grande similitude des matrices de jugements de dissemblance des expériences 1, 2, et 3, obtenus pour des F0 différentes. Le second est la très forte symétrie des matrices de dissemblance des expériences 1-2 et 1-3.

Le premier suggère une grande stabilité des différences de timbre inter-instrument en fonction de la F0. Cette conclusion est aussi suggérée par les analyses multidimensionnelles qui produisent des configurations qui se ressemblent et dont les dimensions sont bien corrélées d'espace à espace. Elle contredit les spéculations pessimistes, faites dans l'Introduction, selon lesquelles un changement de la F0 pourrait entraîner un chamboulement de l'espace des timbres. Elle confirme aussi la généralité des résultats d'études précédentes faites à une F0 particulière (Krumhansl, 1989; McAdams, 1995).

Le deuxième résultat remarquable (symétrie des matrices des expériences 1-2 et 1-3) permet d'aller encore plus loin dans les conclusions, puisqu'elle permet pratiquement de conclure à une invariance du timbre en fonction de la F0. En effet, considérons deux instruments A et B et supposons que chacun se déplace selon une dimension perceptive en fonction de F0. Dans une paire avec F0 différentes le déplacement de l'instrument A affecte la distance perceptive avec l'instrument B. La symétrie de la matrice de dissemblance implique que le déplacement de l'instrument B avec F0 doit affecter de façon égale la distance avec l'instrument A. Cela n'est possible que si (1) ni l'un ni l'autre ne se déplace ou (2) les déplacements se font perpendiculairement au vecteur qui relie les instruments, ou pour toutes les paires façon symétrique de telle façon que les distances restent constantes. Cette deuxième contrainte est incompatible avec un espace à dimensionalité réduite. L'hypothèse d'invariance est confortée par l'analyse des matrices composites, qui montre un très faible déplacement dans l'espace des timbres en fonction de F0.

IV.1) Dépendance du timbre sur la F0

La cohérence entre les résultats des expériences 1, 2 et 3

Le tableau des cohérences, entre les matrices des résultats bruts 1, 2 et 3, montre de bons résultats, environ 0,97 de coefficient de corrélation. Le tableau des cohérences résultats, entre les espaces MDS 1, 2 et 3, entre 0,78 et 0,89 de coefficient de corrélation, montre de bons encore de bons résultats. Les tableaux des corrélations, avec les paramètres physiques, montrent que les premières et les deuxièmes dimensions des expériences sont toutes corrélées aux mêmes attributs physiques, respectivement l'impulsivité, environ 0,95, et le centre de gravité instantané, environ 0,90.

Les trois espaces sont donc proches, bien qu'ils aient été conçus avec des fréquences de fondamentales différentes. Cela indique que le timbre possède une certaine stabilité vis-à-vis de la fréquence fondamentale.

Il est donc permis de penser que si Krumhansl (1989) et McAdams ( 1995) avaient conçu leurs expériences avec les mêmes instruments mais ayant une autre fréquence de fondamentale, les espaces trouvés seraient proches de ceux déjà connus.

La perception des relations perceptives entre timbres possède donc une certaine résistance à la F0, (du moins pour la gamme de F0 testée).

Nous ne sommes pas arrivés à expliquer les petites différences entre les expériences, à savoir si elles sont dues aux bruits, aux changement physiques du son, ou à des effets perceptifs. Il est fort probable que ces trois causes soient présentes, sans que nous puissions en déterminer les pourcentages.

Toutefois, il est intéressant à remarquer que les dimensions 2 des trois espaces sont toutes fortement corrélées au centre de gravité spectral (le cgs), pourtant elles sont moyennement corrélées entre elles.

Si l'impulsivité d'un son reste assez stable le long de sa tessiture, il n'en est pas de même pour son cgs. En effet, celui-ci est fonction de nombreux paramètres, comme les modes propres de son résonateur, la fréquence fondamentale, son harmonicité. Il évoluera donc de façon non linéaire le long de sa tessiture. Chaque instrument fera de même.

Il est donc logique que d'un espace à un autre cette dimension évolue non-linéairement, tout en étant toujours corrélée avec la même dimension physique.

IV.2) Les expériences 1-2 et 1-3

La symétrie des matrices 1-2 et 1-3 est surprenante. Elle indique nettement que les sujets ont été capables de remplir la tâche. En effet, ils sont arrivé à juger deux timbres n'ayant pas la même F0.

Cela ouvre la voie à de nombreuses nouvelles expériences sur le timbre.

Toutefois un doute subsiste : les sujets auraient pu reconnaître les instruments, et juger ainsi deux catégories ou deux famille d'instrument. En effet, un violon aura un aspect visuel plus proche d'une contrebasse, ou d'un violoncelle, qu'une trompette ou un hautbois, quelles que soient les notes jouées.

Les sujets, en entendant la paire clt1 et htb3, auraient pu reconnaître les deux instruments, et ainsi les juger proches. Puis à l'écoute de la paire clt3 et htb1, les sujets auraient de nouveau reconnu les instruments et les juger de la même façon.

La bonne corrélation entre les matrices 1-2 et 1-3, environ 0.99 de coefficient de corrélation , irait dans ce sens.

Afin de lever ce doute, il faudrait analyser les résultats de chaque sujet, en les comparant avec le taux de reconnaissance des instruments. Si les sujets, qui reconnaissent les instruments, possèdent des matrices plus symétriques, que les autres, alors nos conclusions devront être remis en question.

IV.3) Les corrélations des expériences 1-2 et1-3.

IV.3.1) L'expérience 12

Les tableaux, avec les paramètres physiques, montrent que l'espace 1-2 est corrélé aux mêmes dimensions physiques que les espaces 1-2 et 3. Ils laissent penser que l'expérience 1-2, a été effectuée de la même façon que les autres expériences, et que les critères étaient les mêmes. La corrélation de la deuxième dimension et le centre de gravité spectral était même supérieure. Cela rejoint les premières impressions des sujets, qui affirmaient que cette expérience était plus facile à réaliser. Il est possible donc possible que l'effort mentale qui consiste à extraire d'un stimulus son timbre, afin de le comparer avec un autre timbre, aide à la concentration donc à mieux juger les stimulis. Si cette hypothèse, après d'autres études complémentaires, se révélait justifier, elle permettrait de nouvelle méthode d'analyse du timbre.

IV.3.2 L'expérience 1-3

Contrairement à l'expérience 1-2, l'expérience 1-3 nous n'avons pas encore trouvé de paramètre physique étant bien corrélé avec sa deuxième dimension, seulement 0,55 avec le cgs.

Nous pouvons donc émettre plusieurs hypothèses:

- Il existe un nouveau paramètre, encore non testé, qui est corrélé avec cette dimension.

- Nous nous trouvons plutôt face à un espace à une dimension plus spécificités.

- La nouvelle rotation ne superpose pas correctement cette dimension perceptive avec une dimension physique.

L'estimation BIC nous indique clairement que nous trouvons face à un espace à deux dimensions avec spécificités, plutôt qu'un espace à une dimension avec spécificité, -530 contre -300.

IV.3.3) Les stimuli naturels

Plusieurs critiques peuvent être formulées des stimulis utilisés:

- Le violon pizzicato est très différent du reste, il est trop spécifique.

- Les instruments impulsifs diffèrent beaucoup des autres stimulis. Les sons entretenus sont ainsi tous repoussés sur un des cotés de la première dimension.

Il est vrai que le violon pizzicato était trop spécifique, cela vient sans doute de la dilatation temporelle de sa décroissance. Il aurait sans doute été préférable d'utiliser un autre instrument impulsif comme le piano.

Toutefois, si les instruments impulsifs sont effectivement très démarqués sur la première dimension, et de ce fait condensent les instruments entretenus sur une faible largeur, cela reflète une réalité perceptive. Il est donc normal de les intégrer à de telles expériences.

Bien que le temps ait manqué, afin de réaliser toutes les analyses voulus, ces expériences nous ont quand même donné des résultats intéressant.

Il appelle d'autres tests afin de confirmer nos hypothèses.

Pourtant au moment de leurs conceptions, nous étions loin d'être certain que ces expériences puissent nous donner des résultants concluants. Plusieurs facteurs pouvaient intervenir et biaisés fortement nos résultats:

- Les stimuli, à cause de leurs origines naturels ainsi que par leurs durées.

- La tâche, consistant à évoluer deux timbres avec des F0 différentes.

- Les interactions timbre/F0, qui auraient pu nous donner trois espaces complètements différents.

- La durée des expériences, la plupart des sujets effectuer jusqu'à 4 heures d'expérimentations, pouvait provoquer une certaine lassitude biaisant les résultats.

Cependant, même si tout n'a pas pu être encore démontré avec une absolue certitude, plusieurs résultats intéressant ont pu être remarqués :

- La première dimension perceptive serait corrélée avec un descripteur physique lié à une mesure d'impulsivité, prenant en compte l'attaque et la décroissance des sons, plutôt qu'avec un descripteur physique uniquement lié au logarithme d'attaque (Krimphoff 1994).

- Le timbre est relativement résistant vis-à-vis de la fréquence fondamentale. Ce résultat est démontré par les similitudes des espaces 1, 2 et 3.

- Les sujets sont capables de juger deux timbres ayant des F0 différentes, comme semble le montrer la symétrie des matrices 1-2 et 1-3.

Benolken, M. et Swanson, C. (1989) "The effect of pitch-related changes on the perception of sung vowels" J. Acoust.Soc.Am. 87, 1781-1785

Castellengo, M. (1998) "Le timbre causal et couleur sonore" issu du cours de psychoacoustique dans le cadre du DEA ATIAM.

Castellengo, M. (1994) " La perception auditive des sons musicaux", dans "La psychologie de la musique" de Arlette Zenatti, éditée par "Psychologie d'aujourd'hui".

de Cheveigné, A. (1999) "Missing-data model of vowel identification" J. Acoust.Soc.Am. 105, 3497-3508

Dupuis, S. (1999) "Le rôle des transitions legato entre notes dans la reconnaissance des instruments de musique", Memoire de recherche de DEA de Sciences Cognitives sous la direction de S.McAdams et X.Rodet.

Donnadieu, S. (1997) "Représentation mentale du timbre des sons complexes et effets de contexte", thèse dirigé par McAdams, S.

Faure, A. et McAdams, S. (1997) "Comparaison de profils sémantiques et de l'espace perceptif de timbres musicaux" Congrès Français d'Acoustique, Marseille, France, Avril 1997.

Faure, A. et McAdams, S. (en préparation) "Verbal description of musical sounds and their recognition form verbal portraits".

Gottfried, T.(1985): "Intelligibility of vowels sung by a countertenor" J. Acoust.Soc.Am. 79, 124-130

Hajda, J. Kendall, R. Carterette, E. et Harshberger, M. (1996) "Methodological issues in timbre research" Ville: Psychology Press

Kendall, R. Carterette, E. et Hajda, J. (1998) "Perceptual and acoustical Features of Natural and Synthetic Orchestral Instrument Tones" University of California, Los Angeles

Krimphoff, J. (1994) "Analyse acoustique et perception du timbre". D.E.A d'Acoustique Appliquée de l'Université du Maine. Stage effectué à l'IRCAM, sous la responsabilité de Stephen McAdams.

McAdams, S. Winsberg, S. Donnadieu, S. De Soete, G. et Krimphoff, J. (1995) "Perceptual scaling of synthesized musical timbres: common dimensions, specificities, and latent subject classes". Psychological Research,58, 177-192.

McAdams, S. (1994) "Audition : psysiologie, perception et cognition" dans "Traité de psychologie expérimentale" de Richelle, M., édité par "Presse Universitaires de France".

Peeters, G. (1999) "Audio CE for Instrument Description (Timbre Similarity)" ISO/IEC JTC1/SC29/WG11/MEPG99/m5422.

Risset, J.C. (1978) "Hauteur et timbre des sons" rapport de l'Ircam 11/78

Sandell, G. et Chronopoulos, M. (1997), ) "Perceptual constancy of musical instrument timbres; genralizing timbre knowledge across registers"

Singh, P. et Hirsh, I. (1992) "Influence of spectral locus and F0 changes on the pitch and timbre of complex tones" J.Acoust.Soc.Am.92 (5) November 1992, 2650-2661.

Slawson, A. (1967): "Vowel Quality and Musical Timbre as Functions of Spectrum Envelope and Fundamental Frequency" J. Acoust.Soc.Am. 43, 87-101

Smith, B. (1995). "An Environnement for Psychoacoustic Experimentation Using the IRCAM Musical Workstation" Society for Music Perception and Cognition Conference 95, Berkeley, Juin 1995.

Zwicker, E. et Fastl, H. (1990) "Phychoacoustics : Facts and Models" edited by Springer-Verlag, New York

- Greg Sandell Home Page, "http://sparkly.parmly.luc.edu/Sandell", un site détaillé sur l'étude du timbre.

- ADDITIVE, "http://www.ircam.fr/anasyn/additive/index-e.html", contient la documentation du logiciel ADDITIVE créé par l'équipe d'Analyse-Synthèse de l'Ircam.

-MODFORMAT, "http://www.ircam.fr/anasyn/additive/modformat.html" contient la documentation du logiciel MODFORMAT créé par l'équipe d'Analyse-Synthèse de l'Ircam.

- Studio On Line, "http://www.ircam.fr/sol".

- PCM, " http://www.ircam.fr/pcm/pub/", la liste de publication de l'équipe Perception et Cognition Musicales de l'Ircam.