[an error occurred while processing this directive]
Draft mars 11, 1997

Figure 20. front page
[to do: In intro OOI zowel MIDI keynumbers uitgelegd als primitive keuze "on basis of esthetic or pragmeatic grounds" genoemd ]
[to do: use of e.g. in text (forexample, for instance intext, e.g., tussen haakjes) e.g. - e.g., of , e.g., ]
[to do: use of ":" just before code example. ]
[to do: :WARNING, : RULE-OF-THUMB, :SOUNDBYTES styles ]
[to do: meer voorlezen van code bv defclass form ]
[to do: grapje over klasse bewustzijn, engelsen of marx ]
Next to Smalltalk, Lisp has been one of the earliest languages to support an object-oriented style, and many ideas, that can now be found in object- oriented extensions of traditional languages (like C++ ) have developed over the years within the Lisp community. The ideas have come to a consistent and mature definition in CLOS, the Common Lisp Object System. This language replaces many of the precursors (Flavors, Common Loops) and has become widely accepted by users of Common Lisp. It contains, next to standard object-oriented mechanisms (e.g., instantiation and inheritance) more sophisticated concepts (like multiple inheritance, method combination, multi-methods and the meta object protocol) that can become powerful tools in constructing computer music systems and representing musical knowledge. The complexity of the full object oriented extension to Common Lisp can be quite overwhelming, especially when one tries to learn it directly from a concise reference such as Steele (1990)
. Therefore this chapter takes a step by step approach with many small examples, which are constructed for the sake of clarity. The exposé of CLOS constructs is divided into three parts. This first part covers all that is needed to define classes, create objects, and define simple methods that can act on them. It contains enough explanation of the mundane issues to learn to program in a simple object oriented style. The second part will treat more advanced topics like multi-methods and method combination which makes CLOS so much more powerful than other object-oriented languages. After mastering this part the reader will be familiar will all aspects of CLOS that one needs for programming in this language. The third part will show how the CLOS language can be extended in CLOS itself. This meta-approach makes it possible to achieve elegant solutions even when the constructs and mechanisms (e.g., the kind of inheritance) built into the language cannot be used directly for representing the domain in question. Although everyday pedestrian use of CLOS does not often entail working at this level, the concepts of the meta object protocol are of such beauty and power that it will be worthwhile to get acquainted with them a bit. this chapter starts by introducing CLOS and building musical examples from scratch, many Lisp constructs, explained in previous chapters are now assumed to be known. Among them are recursion, the loop macro, lists and arrays, functional arguments, and assignment.
When one uses a general data structure like a list to store information, one has to program a data abstraction barrier. This set of selector functions and constructor functions provides access to parts of the data structure, or builds one, and prevents the programmer from having to remember what e.g the caddar of a certain list represents. In CLOS the main data structure is the object, a record-like concept. The access functions for objects are automatically defined by the system when the type of such an object is defined. There is a rigorous division between an object (an instance) and the type of that object (a class).[1] In a class definition the programmer declares what attributes (slots) an object of that class has and how they are to be accessed. the next example a class note is defined for the representation of a simple note of a specific pitch and duration. [2] It has two slots, a duration (in arbitrary units, e.g., seconds or quarter notes) and a key number[3]class definition is made with a defclass form. Like all def... forms this form has some syntax to remember. First the name of the class to be defined is given, in this case note. Following is a list of classes to inherit from (inheritance will be described later), in this case it is empty. After that, a list of slot descriptors follows. Each slot descriptor is a list of the slot name and some keyword-value pairs that define the name of the accessor function, the name of the initialization keyword by which the slot can be given its initial value and the documentation string describing the slot. The last component of the defclass form are the class options. In this case the only class option is a documentation string which describes the class.
(defclass note ()
((duration :accessor duration
:initarg :duration
:documentation "Duration in time units")
(pitch :accessor pitch
:initarg :pitch
:documentation "Pitch in MIDI numbers"))
(:documentation "Class of note objects with pitch and duration attributes"))
After having defined the class note there is no note object yet: a defclass form is like a type definition. We will have to make an object by instantiating the class using the function make- instance. The first argument to make- instance is the name of a class and the initialization arguments. Thus we can supply values for each attribute, each slot of the note, by listing the corresponding initializationkeyword supplied in the slot descriptor of the class definition, and a value for that slot.
(make-instance 'note :duration 2 :pitch 60)
The expression above will return an object that represents a middle-C note of two time units. This object has its two slots initialized accordingly. If the expression above is too elaborate for your taste or, a better reason, if you want to create notes in your program without fixing yourself to this particular class definition and initializationprotocol yet, a constructor function has to be defined. Contrary to a record definition, a CLOS class definition does not give rise to the automatic generation of a constructur function. Our first attempt at constructing one may look like:
(defun note (&key duration pitch)
"Return a note object with a specified duration and pitch"
(make-instance 'note :duration duration :pitch pitch))
This note constructor function passes its two arguments to make- instance. But to flexibly allow for later extensions, we will define a constructor function that passes its whole argument list, whatever that may be, directly to make- instance. It uses the &rest lambda list keyword by which an arbitrary number of arguments in the function call are gathered in a list. apply takes care to feed the elements of this list as separate arguments to :Lisp make-instance
.
(defun note (&rest attributes)
"Return a note object with specified attributes (keyword value pairs)"
(apply #'make-instance 'note attributes))
The fact that note is used both as the name of a user defined Lisp function, and of a user defined CLOS class does not cause name clashes: it is always clear from the context which construct is intended. Now a note object can be created by calling the note function. As shown after the arrow (->) this evaluates to an object of the note class printed in a not very readable format.
(note :duration 2 :pitch 60)
->
#<NOTE #x3F5BC1>
Later we will show how we can program a play function that can, e.g., transmit the note over MIDI to a connected synthesizer and make it audible.
A note object can be accessed (its slots read) by the accessor functions named in the slot descriptors of the class definition of note. The next example shows the creation of a note with the new constructur function and some subsequent slot access to print its duration and pitch attributes (the double arrow (=>) means "outputs by side effect" or "prints").
(let ((object (note :duration 3 :pitch 65)))
(print (duration object))
(print (pitch object))
object)
=>
3
65
->
#<NOTE #x3F5FB9>
To avoid having to print attributes of notes all the time, for inspection of their values, one can define an external representation of notes in a readable format that directly shows the values of the slots. Here we define a function called show- note. It uses the accessor functions to translate the note and the values of its slots into a readable list. We arbitrarily choose to let it yield the same simple list format that happens to be the construction call [4]. [to do: read macros for note syntax, load forms ]We will need to call this function explicitly for the moment, to show the results of our programming. However, we will tie this function [5] more closely into the system later, such that notes will be printed automatically in this format.
(defun show-note (object)
"Return a list describing a note object with its attributes"
(list 'note :duration (duration object) :pitch (pitch object)))
(show-note (note :duration 2 :pitch 61)) -> (note :duration 2 :pitch 61)
We will enrich our domain of musical objects a bit and, as example, add some classes that handle the representation of time order. You might have noticed that a note object has no slot specifying the time of its onset. We will indeed opt for a relative specification of time: the actual onset of a note will be dictated by its context. There are two obvious time relations that two musical objects can have: they can start at the same time or one can start after the other. Specifying the time relations between objects as being either parallel or sequential[6] and building larger musical objects in that way is an alternative to the use of absolute start times found in most composition systems, but the choice is made here quite arbitrarily - just to illustrate the definition and use of these constructs[7]. Below the definition of two classes is given, one to represent sequential and the other to represent simultaneous musical aggregates. They have only one slot that will be bound to a list of their parts.
(defclass sequential ()
((elements :accessor elements
:initarg :elements
:documentation "The successive components"))
(:documentation "A group of musical objects, one after another"))
(defclass parallel ()
((elements :accessor elements
:initarg :elements
:documentation "The simultaneous components"))
(:documentation "A group of musical objects, starting at the same time"))
After the class definitions we can define the constructor functions for these compound musical objects.
(defun sequential (&rest elements)
"Return a sequential musical object consisting of the specified components"
(make-instance 'sequential :elements elements))
(defun parallel (&rest elements)
"Return a parallel musical object consisting of the specified components"
(make-instance 'parallel :elements elements))
Now more elaborate musical objects can be constructed, like a low long note parallel to a sequence of three higher notes [8].
(defun example ()
"Returns a simple structured musical object"
(parallel (sequential (note :duration 1 :pitch 60)
(note :duration 2 :pitch 63)
(note :duration 1 :pitch 61))
(note :duration 4 :pitch 55)))
Figure 21. Score of the example.
[to do: waar is deze pict gebleven? ]
The score [9] of this example is given in Figure ?. A piano-roll notation of the same musical object is given in Figure ?. On the horizontal axis time runs from left to right, in time units. On the vertical axis pitch is represented. Each rectangle [10]represents a note.
(draw (example)) =>
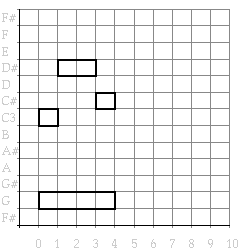
Figure 22. Piano-roll notation of the example.
When the body of example is run, three note objects will be created and collected in a list which is stored in the elements slot of an encompassing sequential object. A list of this sequential object together with a fourth lower note is stored in the elements slot of the enclosing parallel object. Thus a structured (parallel or sequential) musical object has access to its parts: they are listed as elements. The musical structures define a part-of hierarchy of linked musical objects. This is illustrated in the tree diagram in Figure ?, which constitutes an alternative graphical representation of the same example.
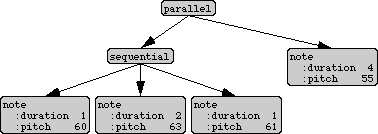
Figure 23. The objects and their links in the example.
In this diagram the arrow represents the "has-part" relation. It reflects the fact that a sequential or parallel object can get access to its parts via its elements slot, but not vise versa.
To make the pitches in our examples a bit easier to read we can translate pitch names to MIDI numbers and vise versa. The two functions pitch- name- to- midi- number and midi- number- to- pitch- name are given as a separate project in section 5.?: pitch names. [to do: make this chapter] They do simple string processing and constitute nothing interesting[11] from the point of CLOS constructs. Let us first check their workings.
(pitch-name-to-midi-number "C#4") -> 73
(midi-number-to-pitch-name 60) -> "C3"
The show- note function can easily be adapted to do the translation and show pitches by name. We can integrate the translation into the note function by changing the pitch argument in the initialization argument list passed to make- instance. This may , e.g., be done destructively, as is shown in the new function definition of note. The small effort needed to define a constructor function for notes now already has proven its worth, by allowing for this addition.
[to do: als er een soort non-destructive modify/substitute is, uit vorig hoofdstuk, op property lists dan die gebruilken ]
(defun note (&rest attributes)
"Return a note object with specified attributes (keyword value pairs)"
(when (stringp (getf attributes :pitch))
(setf (getf attributes :pitch)
(pitch-name-to-midi-number (getf attributes :pitch))))
(apply #'make-instance 'note attributes))
(defun show-note (object)
"Return a list describing a note object with its attributes"
(list 'note
:duration (duration object)
:pitch (midi-number-to-pitch-name (pitch object))))
(pitch (note :duration 2 :pitch "C#3"))
->
61
(show-note (note :duration 2 :pitch "C#3"))
->
(note :duration 2 :pitch "C#3")
One might wonder why we didn't store pitch names directly in the pitch slot of the note. There wouldn't be anything fundamentally wrong with this, except for the fact that the calculations on pitches that we are going to write later (like transpositions) are much easier to implement on a numeric representation.[12]
Now we will introduce one of the corner stones of object-oriented programming: polymorphism. We start with the observation that our structured musical objects have no readable representation yet.
(example)
->
#<PARALLEL #xEC7439>
To be able to show the new objects in a readable form on the output as well, one could be tempted to define show- sequential and show- parallel functions, similar to the show- note function, to construct the appropriate lists. In calling these functions the programmer then has to be aware of the type of musical objects to show and select the proper function. E.g., when the musical object is parallel (like example) show- parallel has to be applied. A better approach would be to write a general show function that can be applied to any type of musical object, obtains the type (class) of its argument and dispatches accordingly to the appropriate code. This could also enable the function to recursively call because they can have elements of an arbitrary type. This approach is illustrated in the next example.
(defun show (object)
"Return a list describing a musical object with its components or attributes"
(typecase object
(note (list 'note
:duration (duration object)
:pitch (midi-number-to-pitch-name (pitch object))))
(sequential (cons 'sequential
(mapcar #'show (elements object))))
(parallel (cons 'parallel
(mapcar #'show (elements object))))))
And indeed, the construction of a so called polymorphic or generic show function that can be applied to many types of musical objects is part of the answer. The first step is to write a CLOS generic function, effectively the same as the function written above, but with some different syntax: now each clause to be executed for a specific class of object is separated out as a so called method. For each method the argument list is given again, but annotating the argument with its type. Don't be put off by the syntactical complexity of this form: we will shortly have the system assemble this monster for us. [13]
(fmakunbound 'show)
(defgeneric show (object)
(:method ((object note))
(list 'note
:duration (duration object)
:pitch (midi-number-to-pitch-name (pitch object))))
(:method ((object sequential))
(cons 'sequential
(mapcar #'show (elements object))))
(:method ((object parallel))
(cons 'parallel
(mapcar #'show (elements object))))
(:documentation "Return a list describing a musical object"))
One of the central ideas of object-oriented programming is the notion of automatic type-driven dispatching, in which the system assembles definitions like the one above from small parts of code written by the programmer. How does this work? We just have to define a set of functions all with the same name, but with different type information for the arguments. These are called methods. Thus three different show methods are to be defined by us, all with the same name but with their argument declared to be of a different class.
(defmethod show ((object note))
"Return a list describing a note object with its attributes"
(list 'note
:duration (duration object)
:pitch (midi-number-to-pitch-name (pitch object))))
(defmethod show ((object sequential))
"Return a list describing a sequential musical object with its components"
(cons 'sequential
(mapcar #'show (elements object))))
(defmethod show ((object parallel))
"Return a list describing a parallel musical object with its components"
(cons 'parallel
(mapcar #'show (elements object))))
These three chuncks of code achieve the same effect as the bulky degeneric form. Silently the system has, when these method definitions are evaluated, assembled a so called generic function show similar to the definition of show- object given above, but calling the appropriate user-defined show methods. The three show methods are said to be specialized to the note, sequential, and parallel class respectively. The show method for a note returns a list with the attributes, with the atom note in front. The show method for a sequential or parallel object collects the result of showing its elements in a list and places the proper atom in front. We should test the show method now, which is done more easily by pretty-printing its result.
(pprint (show (example)))
=>
(parallel (sequential (note :duration 1 :pitch "C3")
(note :duration 2 :pitch "D#3")
(note :duration 1 :pitch "C#3"))
(note :duration 4 :pitch "G2"))
Note how the show methods for sequential and parallel objects call themselves recursively using a functional argument to mapcar to calculate the result for each element. Because in CLOS the individual methods are combined into a generic function automatically, the well-known functional programming techniques like recursion, and passing functions as arguments to other functions, can be applied directly for use on methods. This unification of functional and object oriented programming using generic functions is a large advantage over the message passing style. In the latter paradigm objects are being send messages (a special language construct) by other objects. This means that all facilities and constructs developed for functions (mapping, combinators, tracing, etc.) have to be redefined to be useful for messages. In CLOS, methods are applied to objects just like functions are applied to arguments, and all the functional paraphernalia works as well for methods.
In a call to show, the so called applicable method is selected by the system, on the basis of the class of the argument. This has the added advantage that when a program grows and more classes are added, the programmer does not have to modify the functions to handle these data types as well, only additional methods have to be defined. We will demonstrate this by adding a class for a rest and the constructor for it (which will be called pause to prevent a name clash with the Lisp rest function which gives the cdr of lists).
(defclass pause ()
((duration :accessor duration
:initarg :duration
:documentation "Duration in time units"))
(:documentation "Class of rest objects with a duration attribute"))
(defun pause (&rest attributes)
"Return a rest object with specified attributes (keyword/value pairs)"
(apply #'make-instance 'pause attributes))
A rest only needs a duration attribute[14]. Adding the following simple method definition will enable compound musical objects that contain rests to be shown as well:
(defmethod show ((object pause))
"Return a list describing a rest object with its attributes"
(list 'pause :duration (duration object)))
Having set up a simple system of musical objects, a way to create them, and a way to print them textually, we can proceed in defining some useful musical transformations on these objects. The next example defines a method that takes a note as argument and creates a new one with a pitch that is transposed by an interval. This method is specialized in one argument, the object to transpose. The second argument of the transpose method, the interval, is not typed (i.e. any type of object will apply). In the example a C# is transposed by a whole tone.
(defmethod transpose ((object note) interval)
"Return a note with a pitch raised by interval"
(note :duration (duration object)
:pitch (+ (pitch object) interval)))
(show (transpose (note :duration 2 :pitch "C#") 2))
-> (note :duration 2 :pitch "D#")
The example above did instantiate a new note object with its duration slot copied directly from the original. This is a proper (non destructive) functional style of programming. But when the original is no longer needed somewhere else, it may make sense to alter one slot in the original itself, instead of creating a new object. And indeed the imperative style of programming in which objects are modified destructively is often used in object oriented programming. In this style one has to take much more care that an object that is altered is not accessible from parts of the program that assume that its state is invariant.
The slots of an object can be destructively written by the generalized setf assignment construct using the same accessors as are used for reading. The next example transposes a note by altering its pitch slot.
(defmethod transpose ((object note) interval)
"Raise the pitch of a note by an interval"
(setf (pitch object) (+ (pitch object) interval)))
Of course the predefined modification macro's that are based on setf, like incf, work as well for slots.
(defmethod transpose ((object note) interval)
"Raise the pitch of a note by an interval"
(incf (pitch object) interval))
To illustrate the workings of the transpose method we show a note before and after transposition.
(let ((object (note :duration 2 :pitch "C#3")))
(print (show object))
(transpose object 3)
(print (show object))
t)
=>
(note :duration 2 :pitch "C#3")
(note :duration 2 :pitch "E3")
Because transpose works by side-effect, it is not really necessary to make it return a value. But often a nicer style of code can result when these destructive transformations do return their modified argument as result.[15] This is a specific style of writing destructively: a function may destroy its arguments but cannot be trusted to update them meaningfully. However, it returns a proper value. This style resembles the protocol that many Common Lisp functions use (e.g., sort). It stands in contrast to the style that uses procedures to modify arguments directly, and whose return value can be ignored.
(defmethod transpose ((object note) interval)
"Raise the pitch of a note by an interval"
(incf (pitch object) interval)
object)
(show (transpose (note :duration 2 :pitch "C#") 3))
->
(note :duration 2 :pitch "E3")
Now, of course, we can define the other methods for transpose as well, using recursion to transpose the components of sequential and parallel musical objects.
(defmethod transpose ((object pause) interval)
"Transpose a rest, do nothing to it"
object)
(defmethod transpose ((object sequential) interval)
"Transpose a sequential musical structure, by transposing its components"
(loop for element in (elements object)
do (transpose element interval))
object)
(defmethod transpose ((object parallel) interval)
"Transpose a parallel musical structure, by transposing its components"
(loop for element in (elements object)
do (transpose element interval))
object)
The compiler will warn that in the transpose method for pause the interval argument is not used. A declaration can instruct the compiler[16], to ignore this parameter and will suppress the warning.
(defmethod transpose ((object pause) interval)
"Transpose a rest, do nothing to it"
(declare (ignore interval))
object)
With our generic definition of transpose and the show facility we can now check its working.
(pprint (show (transpose (example) 2)))
=>
(parallel (sequential (note :duration 1 :pitch "D3")
(note :duration 2 :pitch "F3")
(note :duration 1 :pitch "D#3"))
(note :duration 4 :pitch "A2"))
This transformation can of course also be checked by playing the results using the play function. In Figure ? the original example plus its transposition is shown, collected together in a sequential order. Figure ? gives the corresponding piano roll notation.
Figure 24. Score of the example and a transposition over a whole tone.
(draw (sequential
(example)
(pause :duration 1)
(transpose (example) 2))) =>
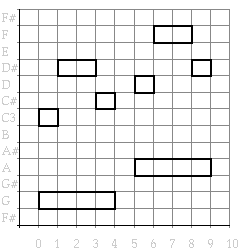
Figure 25. The example and its transposition over a whole tone.
You may have wondered whether sequential and parallel really need their own definitions of transpose, even though the body of the method is exactly the same. The same holds for the duplicated definition of the elements slot in the sequential and parallel class. An indeed, in the object-oriented style one strives towards sharing duplicated code as much as possible. This is done is by making the sharable part explicit as a new abstract class that we will call compound- musical- object. It has its own slot definition and a transpose method defined for it. An abstract class is not intended for direct initialization; it only groups the shared behavior (in this case a slot definition and the transpose method) together, such that other classes can inherit this behavior without defining it themselves.
(defclass compound-musical-object ()
((elements :accessor elements
:initarg :elements
:documentation "The components"))
(:documentation "A group of musical objects ordered in time"))
(defmethod transpose ((object compound-musical-object) interval)
"Transpose a compound musical structure, by transposing its components"
(loop for element in (elements object)
do (transpose element interval))
object)
Inheriting this class' behavior is done by supplying the class in the list of direct superclasses in the defclass form of sequential and parallel. This is the first list after the method's name, the list that unto now had been left empty.
(defclass sequential (compound-musical-object) ()
(:documentation "A group of musical objects, one after another"))
(defclass parallel (compound-musical-object) ()
(:documentation "A group of musical objects, starting at the same time"))
These definitions show that the duplicated slot descriptors in the definition of the sequential and parallel class are indeed no longer necessary. The duplicated transpose methods of these two classes have become redundant as well. A graphical representation of the inheritance in the form of a class hierarchy is quite useful, especially when the situation becomes more complex. For the moment we have just 2 concrete classes which inherit from the same abstract one. In Figure ? these classes are shown with the arrows representing their directly-inherits-from relation. This is the inverse of the is-direct-superclass-of relation. The concrete classes (that can be instantiated directly) are shown in a gray shade.

Figure 26. Inheriting transposition behavior for compound musical objects.
The inheritance diagram above is annotated with the transpose method defined for these different classes. We see that, next to the new general transpose method that was defined for all compound musical objects, the now redundant old transpose definitions for parallel and sequential object are still around. In the selection of an applicable method the so called most specific method will be chosen to run. This is, roughly spoken, the one encountered first when one starts at the class of the object in the inheritance hierarchy and moves upward. Thus any parallel or sequential object will still be transposed with its old definition that was defined for that specific class, not with the method specialized for the less specific compound musical objects. The old methods are said to shadow the new one. In general the use of shadowing can be correct and intended by the programmer-, but often it signals a flaw in the design of the classes -an inelegant partitioning of knowledge, and it is hard to keep track of the complexities of inheritance when shadowing is used a lot. In our case the unintended shadowing resulted because old method definitions were still around. Removing these old method definitions in de editor textually does not remove them from the system. The difference between the textual state in the editor and the internal state of the system, which can be a source of great confusion, is managed best [17] by keeping all method definitions together and starting afresh after these kinds of large changes. This is done by removing all old method definitions using fmakunbound, before evaluating new ones.
(fmakunbound 'transpose)
(defmethod transpose ((object compound-musical-object) interval)
"Transpose a compound musical structure, by transposing its components"
(loop for element in (elements object)
do (transpose element interval))
object)
(defmethod transpose ((object pause) interval)
"Transpose a rest, do nothing to it"
(declare (ignore interval))
object)
(defmethod transpose ((object note) interval)
"Raise the pitch of a note by interval"
(incf (pitch object) interval)
object)
Thus the definition of the transpose method for sequential or parallel objects is disposed of, because it is handled by the transpose method specialized for compound- musical- object, and the system will find this method to apply to an object of type sequential or parallel because no other, more specific, methods are available. We can similarly cleanup the definition of note and pause to inherit their shared duration slot from a new class for basic (non-compound) musical objects. And it even makes sense to provide an abstract class musical- object for (yet unforeseen) behavior that will be shared by all musical objects. This leads to the following class definitions. [18]
(defclass musical-object () ()
(:documentation "The abstract root class of all musical objects"))
(defclass compound-musical-object (musical-object)
((elements :accessor elements
:initarg :elements
:documentation "The components"))
(:documentation "A group of musical objects ordered in time"))
(defclass sequential (compound-musical-object) ()
(:documentation "A group of musical objects, one after another"))
(defclass parallel (compound-musical-object) ()
(:documentation "A group of musical objects, starting at the same time"))
(defclass basic-musical-object (musical-object)
((duration :accessor duration
:initarg :duration
:initform 1
:documentation "Duration in time units"))
(:documentation "A primitive musical object with a duration attribute"))
(defclass note (basic-musical-object)
((pitch :accessor pitch
:initarg :pitch
:initform 60
:documentation "Pitch in MIDI numbers"))
(:documentation "A pitched note"))
(defclass pause (basic-musical-object) ()
(:documentation "A rest"))
Now we have created a more complex class hierarchy which reflects our view of musical objects and their shared characteristics. It can be depicted as a directed a-cyclic IS-A network of directly-inherits-from relations, as in Figure ?. In this hierarchy, each class inherits only from one other class. More elaborate examples of inheritance will be given later. Note that this figure depicts the general IS-A relation between classes, in contrast to Figure ? which shows the HAS-PART pointers between real instantiated objects.

Figure 27. The hierarchy of classes for musical objects.
Again we can show some method definitions in this tree to see where the knowledge [19] needed to show and transpose different types of musical objects resides. Figure ? illustrates how each instantiable class has its own show method. pause and note have their own transpose definition, but whenever transpose is applied to a sequential or parallel object, the applicable method selected by the system to run, is the method definition specialized to compound musical objects.

Figure 28. The method definitions of transpose and show.
Now we will reveal a bit more of the protocol that governs how a new object is instantiated and initialized. In the slot descriptors given in the class definitions above, you may have noticed a new slot option :initform. This indicates that when an instance is made (with make- instance) without supplying an initialization argument for a certain slot, this value will be used instead. It gives a default value for the slot, e.g., the duration slots default to 1 second. Because our note and pause constructor functions pass their whole argument list to make- instance, they do not interfere with this mechanism. And any incomplete call to create a musical object will result in an object with all of its slots bound, some by specification, some by default.
(show (pause)) -> (pause :duration 1)
(show (note :duration 4)) -> (note :duration 4 :pitch "C3")
This is the first place where we encounter the possibility of declaring default values. In CLOS there are many mechanisms like these available, and the understanding of their proper use, and of their interaction can be quite difficult. We save this topic for the next chapter.
Lisp looks like an untyped language: the programmer never has to declare the type of a variable as in other languages. But actually all Lisp data structures carry their type with them and all primitive functions check the type of their arguments before they are run. Thus e.g., the application of 1+ to a list will neatly trigger an error. It is thus better to say that Lisp is a dynamically typed language. In constrast to most language which are statically typed and that check for type correctnness at compile time, the type checks are performed at run time. The penalty of run time type checking (slower execution) has been used often as an argument against the use of Lisp. For Common Lisp this argument has become completely unappropriate, since by annotating functions with type declarations the compiler will do the type checking at compile time, and leave out the run time checks. Thus the programmer can quickly write untyped code and, after debugging, add the type declaration which will make it run faster. [to do: This topic is elaborated further in ?? ]
Before CLOS existed, Common Lisp had already an elaborated type system for data structures like numbers, lists, records and arrays. The new class construct of CLOS had to be integrated somehow into this system, this was done by having any CLOS class definition automatically imply the definition of a new Lisp type. Objects that are instantiations of a certain class thus automatically have a certain Lisp type and can e.g. be tested using the type- of and typep functions.
(type-of (example))
->
parallel
(typep (example) 'note)
->
nil
This allows for another definition of the predicates to test a musical object for its class. Let us list the type predicates for all of our concrete (instantiable) classes.Later we will introduce a way to have the class definition define these methods automatically, much like record type definitions do. [to do: verwijzing naar meta-object-auto-type-prediactes in de voetnoot zetten]
Because it might be usefull to check any lisp object if it is of a certain class, we specialize on type t, the type of any lisp object, numbers, lists and instantiations alike. Instead of specializing the argument to t, we could have left it unspecialized as well or we could have defined a function instead of a method, these forms are similar. As a final refinement we can have the predicate return something useful instead of t. Because in Lisp anything non-nil is considered true, this refinement is backwards compatible with old definitions which returned t or nil, while extending the usfulness, e.g., in search functions.
(defmethod note? ((object t))
"Return the object if it is an instantiation of class note, nil otherwise"
(when (typep object 'note) object))
(defmethod pause? ((object t))
"Return the object if it is an instantiation of class pause, nil otherwise"
(when (typep object 'pause) object))
(defmethod sequential? ((object t))
"Return the object if it is an instantiation of class sequential, nil otherwise"
(when (typep object 'sequential) object))
(defmethod pause? ((object t))
"Return the object if it is an instantiation of class parallel, nil otherwise"
(when (typep object 'parallel) object))
One last remark, before we continue defining more interesting methods: whenever your code makes calls to these type predicates, you might not be using the object oriented style to its full extend. Since the system can automatically execute different pieces of code depending on the type of objects, there is often no need to write addditional code that calls type predicates in deciding which code to run.
It would be nice if our external representation in list form, as produced by the show method, could be used for all printing (instead of the unreadable #<...> format). The Common Lisp system already incorporates a print- object method for the predefined data types (array's, records etc.) which is called in all printing. We can link our own way of showing the musical objects directly into the system by defining a print- object method for musical- object, which takes care of pretty-printing as well.
(defmethod print-object ((object musical-object) stream)
"Prints a description of a musical object as a list to a stream"
(pprint (show object) stream))
After this, all printing is done via our print- object method, be it by calls to print or format, in traces and error messages, or in the top-level read-eval-print loop in which the user types an expression to the interpreter and the evaluated result is printed by the system:[20]
(example)
->
(parallel (sequential (note :duration 1 :pitch "C3")
(note :duration 2 :pitch "D#3")
(note :duration 1 :pitch "C#3"))
(note :duration 4 :pitch "G2"))
This illustrates an important advantage of object-oriented style: the ease of extending code of which the source is not available - we even elaborated a system-defined primitive here. It also shows a constraint on this approach: the argument list of the definition of a method must be known, because they must be similar for all methods. That is, all method definitions with the same name have to have congruent lambda lists in which only the types of the argument (and the names) may vary. Further treatment of this topic is given in Steele (1990, page 791)
.
The intuition, that a class which can handle things common to all kinds of musical objects might come in handy one time, thus proved to be right: the print- object method is specialized to this general class. The skill to design class hierarchies for a domain, such that later extensions fit in easily, can only be developed during the construction and re-construction of many object oriented programs. Or, in other words, while object oriented programming languages are very flexible and dynamic, and code can often be re-used and extended instead of being re-written, the modification of class hierarchies can entail many complex changes throughout the program. And thus a proper design of these definitions from the start, with enough hooks for adding unforeseen behavior later, is an essential habit.
Because the transformations on musical objects are done destructively, we need a facility to copy a musical object, in case the original is needed as well. To realize this, we simply extract the attributes of a note and create a new note with the same attributes, and make copies of the elements for sequential and parallel objects.[21]
(defmethod copy-object ((object note))
"Return a copy of a note object"
(note :duration (duration object) :pitch (pitch object)))
(defmethod copy-object ((object pause))
"Return a copy of a pause object"
(pause :duration (duration object)))
(defmethod copy-object ((object sequential))
"Return a copy of a sequential object, recursively copying its elements"
(apply #'sequential (mapcar #'copy-object (elements object))))
(defmethod copy-object ((object parallel))
"Return a copy of a parallel object, recursively copying its elements"
(apply #'parallel (mapcar #'copy-object (elements object))))
Alternatively, since we already defined a show method, which delivers a description that resembles the expression that created the musical object directly, copying can be implemented as evaluating the result of the show method:[22]
(fmakunbound 'copy-object)
(defmethod copy-object ((object musical-object))
(eval (show object)))
We will now continue with defining some useful transformations, using the programs we have made so far. We will write a function that applies an arbitrary transformation to a musical object, and returns the result preceded by the original and separator (e.g., a rest):
(defmethod original-and-transform ((object musical-object)
separator transform &rest args)
"Return a sequence of the original, a separator, and a transformed object"
(let ((result (apply transform (copy-object object) args)))
(if separator
(sequential object separator result)
(sequential object result))))
(original-and-transform (note :duration 1 :pitch "C3")
(pause :duration 1)
#'transpose 2)
->
(sequential (note :duration 1 :pitch "C3")
(pause :duration 1)
(note :duration 1 :pitch "D3"))
Other functions that combine musical objects can be written as well, e.g., functions to create a repetition and a canon. The results of these functions can be safely subjected to destructive transformations because duplicated objects are copied: there is no shared structure.
(defmethod repeat ((object musical-object) &optional (n 2) separator)
"Return a number of repetions of a musical object"
(apply #'sequential
object
(loop repeat (1- n)
when separator collect (copy-object separator)
collect (copy-object object))))
(defmethod canon ((object musical-object) n onset-delay)
"Return an n-voiced canon of a musical object"
(apply #'parallel
(loop for voice from 0 below n
collect (sequential
(pause :duration (* voice onset-delay))
(copy-object object)))))
These functions can now be used to create a familiar canon. [23]
[to do: tekst en noten checken ]
(defun frere-jacques ()
(sequential (note :pitch "C3")
(note :pitch "D3")
(note :pitch "E3")
(note :pitch "C3")))
(defun dormez-vous ()
(sequential (note :pitch "E3")
(note :pitch "F3")
(note :pitch "G3" :duration 2)))
(defun sonner-la-matine ()
(sequential (note :pitch "G3" :duration 1/2)
(note :pitch "A3" :duration 1/2)
(note :pitch "G3" :duration 1/2)
(note :pitch "F3" :duration 1/2)
(note :pitch "E3")
(note :pitch "C3")))
(defun bim-bam-bom ()
(sequential (note :pitch "C2")
(note :pitch "G2")
(note :pitch "C2" :duration 2)))
(defun frere-jacques-voice ()
(sequential (repeat (frere-jacques))
(repeat (dormez-vous))
(repeat (sonner-la-matine))
(repeat (bim-bam-bom))))
(defun frere-jacques-canon ()
(canon (frere-jacques-voice) 4 8))

Figure 29. The Frere Jacques canon.
[to do: could go somewhere else to enlighthen, when needed: gebruikt geen OO of afhankelijkheden ]
To give some hints how generative aspects can be implemented elegantly within our framework, we will write some functions that produce a rhythm that is strictly metric. That is, every note starts of one of the levels of the metric hierarchy. Or, to say it in other words, every level is either completely divided or presented as one whole.[24] We first write a program that recursively divides a time duration, using a different divisor at each level, and deciding at random whether subdivision has to continue. This function can be said to embody some kind of generative grammar, deciding at random which of the alternative generative rules (i.e., set of divisors) to use. A toss function, that returns t for a specified fraction of the times that it is called, is a handy building block.
(defun toss (chance)
"There is a chance that this will return t"
(< (random 10000) (* chance 10000)))
(defun strictly-metric-division (duration divisors)
"return a list of strictly metric durations"
(if (and divisors (toss .75))
(loop repeat (first divisors)
append (strictly-metric-division (/ duration (first divisors))
(rest divisors)))
(list duration)))
Figure ? shows the time interval division as produced by the strictly- metric- division function.
(strictly-metric-division 12 '(2 3 2))
->
(1 1 2 1 1 6)

Figure 30. A typical metric division of time intervals
[to do: beter snappen waarom tree draw niet precies goed de sizes uitrekent, is nu een truc ]
The results of the strictly- metric- division have to be mapped to a sequence of notes. Generating a bar of notes in a certain time-signature can now simply be described as a bar of a certain duration and its subdivision (at each level) given as arguments to the strictly metric generator.
(defun make-rhythm (durations)
"Return a sequence of notes with given durations"
(apply #'sequential (loop for duration in durations
collect (note :duration duration))))
(defun bar-strict-3/4 ()
"Return a bar of notes in strict 3/4"
(make-rhythm (strictly-metric-division 3/4 '(3 2 2))))
(defun bar-strict-6/8 ()
"Return a bar of notes in strict 6/8"
(make-rhythm (strictly-metric-division 6/8 '(2 3 2))))
(bar-strict-6/8)
->
(sequential (note :duration 3/8 :pitch "C3")
(note :duration 1/16 :pitch "C3")
(note :duration 1/16 :pitch "C3")
(note :duration 1/8 :pitch "C3")
(note :duration 1/16 :pitch "C3")
(note :duration 1/16 :pitch "C3"))
[to do: Hier een keer een score generen met 6/8 indicatie en beaming en vast weergeven (:eval? nil) met de aanroep (play (bar-strict-6/8)) ]
To study another transformation, and see how it differs from transposition, consider a transformation that inverts a piece: reflecting the pitches of all the notes around a pitch center. For a compound musical objects this amounts to recursively applying the mirror transformation to all its elements, for a note the method needs to calculate the reflected pitch and update the pitch slot of the note, for a rest the method will do nothing.
(defmethod mirror ((object compound-musical-object) center)
"Reflect all pitches occurring in a compound musical object around a center"
(loop for element in (elements object)
do (mirror element center))
object)
(defmethod mirror ((object note) center)
"Reflect the pitch of a note around a center"
(setf (pitch object)
(- center
(- (pitch object) center)))
object)
(defmethod mirror ((object pause) center)
"Reflect a rest: do nothing to it"
(declare (ignore center))
object)
In Figure ? the result of this transformation is shown, applied to the example and preceded by the original.
(draw (original-and-transform
(example)
(pause :duration 1)
#'mirror 60)) =>
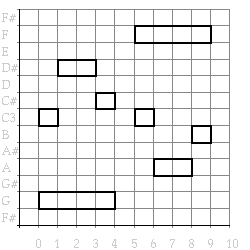
Figure 31. The example and an inversion around middle-c.
The body of the mirror method for notes still is a bit too complex to our taste.[25] An auxiliary function can easily do the arithmetic on pitches. A natural name for this function would be mirror of course. But then we need to make it into a real method and specialize it for a certain kind of data. Because CLOS is well-integrated in the Lisp type system, we can use ordinary types as specializers for methods as well. This means that on any Lisp data type (e.g., number, string or array) specialized methods can be defined, just as easy as for real classes. We will use this facility to write a mirror method specialized for numbers, and call that method inside the method specialized for notes.
(defmethod mirror ((pitch number) center)
"Reflect a pitch around a center"
(- center (- pitch center)))
(defmethod mirror ((object note) center)
"Reflect the pitch of a note around a center"
(setf (pitch object) (mirror (pitch object) center))
object)
To allow naming of center pitches we need to check for strings and translate them into numbers before we apply the arithmetic.[26]
(defmethod mirror ((pitch number) center-pitch)
"Reflect a pitch around a center"
(let ((center (if (stringp center-pitch)
(pitch-name-to-midi-number center-pitch)
center-pitch)))
(- center (- pitch center))))
(defmethod mirror ((object note) center)
"Reflect the pitch of a note around a center"
(setf (pitch object)
(mirror (pitch object) center))
object)
There is one last sideline that we will make before we continuing with CLOS. We noticed that in the definition of transpose, incf was used to update the pitch slot of an object with the sum of its old value and a specified interval. And instead of (setf (pitch object)(+ (pitch object) interval) we wrote (incf (pitch object) interval). Of course this mechanism is what we need here as well: a mirrorf macro to update a generalizedvariable, like a slot, directly with our user-defined mirror method for numbers. Writing the macro to achieve this is not trivial, even though it may look otherwise.[27] However, Common Lisp provides a facility that can define the macro for us. The define- modify- macro macro needs a name, a list of extra arguments, a function that calculates a new value, some extra arguments, and a documentation string.
(define-modify-macro mirrorf (center)
mirror
"Change a variable by reflecting it around a certain center")
Now we may use this modification macro in the body of the mirror method for notes.[28]
(defmethod mirror ((object note) center)
"Reflect the pitch of a note around a center"
(mirrorf (pitch object) center)
object)
Figure 32. The example and its inversion.
When working with structures of objects that are linked to one another (like via the elements slot of the compound musical objects), one tends to find that many programs exhibit more or less the same way of visiting the different objects of such a structure. Compare, e.g., the mirror program and the definition of transpose, repeated below.
(defmethod mirror ((object compound-musical-object) center)
"Reflect all pitches occurring in a compound musical object around a center"
(loop for element in (elements object)
do (mirror element center))
object)
(defmethod transpose ((object compound-musical-object) interval)
"Transpose a compound musical structure, by transposing its components"
(loop for element in (elements object)
do (transpose element interval))
object)
You can see that both have the same control structure. To extract that functionality we could write something that is like mapc is for lists: a general mapping function that applies the operation to each element of a compound musical object. To add some more generality, we will have the new function pass any extra arguments that it receives to the operation, as well.
(defmethod mapc-elements ((object compound-musical-object) operation &rest args)
"Apply the operation to each element in a musical object"
(mapc #'(lambda(element)(apply operation element args))
(elements object))
object)
mapc- elements, when applied to a compound musical object, applies an operation to each of its elements. Of course it could have been written as well using the loop construct, the choice is a matter of taste. We will choose to use the later construct in these situations.
(defmethod mapc-elements ((object compound-musical-object) operation &rest args)
"Apply the operation to each element in a musical object"
(loop for element in (elements object)
do (apply operation element args))
object)
Thus we can define transpose and mirror (and a whole bunch of similar transformations) much more concise.
(defmethod transpose ((object compound-musical-object) interval)
"Transpose all pitches occurring in a musical object over an interval"
(mapc-elements object #'transpose interval))
(defmethod mirror ((object compound-musical-object) center)
"Mirror all pitches occurring in a musical object around a center"
(mapc-elements object #'mirror center))
A different kind of iterator is needed when the walk through the elements may be terminated prematurely, and a result has to be returned. This typically is the case in functions that search through a structure and return T as soon as an encountered object satisfies some predicate. As an example we will test whether our example musical object contains a note as one of its elements (it does).
(defmethod find-element ((object compound-musical-object) predicate &rest args)
"Return the first element which satifies a predicate, NIL if none do"
(loop for element in (elements object)
thereis (apply predicate element args)))
(find-element (example)
#'note?)
->
(note :duration 4 :pitch "G2")
Of course the predicates can be more complex and may even be constructed on the fly.
(find-element (example)
(compose-and #'note?
#'(lambda(note)
(> (duration note) 3))))
->
T
In the definition above we cleverly returned the value returned by the predicate, whenever it is not NIL. This allows for a predicate that returns some meaningfull value whenever it is satisfied,, e.g., the object that satisfies it. In the next example such a predicate is composed by adding the identity function as the last component.
(find-element (example)
(compose-and #'note?
#'(lambda(object)(> (duration object) 3))
#'identity))
->
(note :duration 4 :pitch "G2")
Using find- element recursively (i.e., not only apply it to the top-level elements of the example) yields a more general search function that can search through as whole musical object and return the first object in the part-of hierarchy that satisfies a certain condition.
(defmethod find-musical-object ((object compound-musical-object) predicate
&rest args)
"Return object when it satifies the predicate, or first such sub-..-sub-object"
(or (apply predicate object args)
(apply #'find-element object #'find-musical-object predicate args)))
(defmethod find-musical-object ((object basic-musical-object) predicate
&rest args)
"Return object when it satisfies the predicate"
(apply predicate object args))
To test our search function we compose a predicate which will return its argument whenever it is applied to a note object with a pitch above middle C.
(find-musical-object (example)
(compose-and #'note?
#'(lambda(note)(> (pitch note) 60))
#'identity))
->
(note :duration 2 :pitch "D#3")
In designing inheritance networks it is always good to check if behavior defined for a specific class can be generalized to others. An example is the duration slot of basic musical objects that can be accessed by the duration method generated by the system. This accessor was generated automatically because duration was defined as an accessor in the slot descriptor in the definition of the basic- musical- object class. Because the duration accessor is itself a method we can extend its applicability by defining methods to calculate the duration of other musical objects. Calling duration on a note or a pause will invoke the proper method and return the value of the slot and calling it on a sequential (or parallel) object should now calculate the sum (or maximum) of the duration of its elements.
(defmethod duration ((object sequential))
"Return the duration of a sequential musical object"
(loop for element in (elements object)
sum (duration element)))
(defmethod duration ((object parallel))
"Return the duration of a parallel musical object"
(loop for element in (elements object)
maximize (duration element)))
(duration (example)) -> 4
This illustrates the advantages of the uniform way of slot access and method calls. The duration method can be applied to any musical object now, without having to remember whether a slot access or a calculation has to be done to retrieve it. This enables easy changes of implementation of the duration concept in the program as well (from stored to calculated, from procedural to declarative), without having to rewrite the parts that use it.
The same mechanism can be used to get an objects' attribute value in a different format. E.g. the frequency of a note (in Hz.) might be of interest. Writing a method to retrieve it looks the same as a slot accessor from the outside. Thus we need not worry whether pitches or frequencies are stored in a note slot, they both can be retrieved in the same way.[29] The auxiliary pitch- to- frequency arithmetic is given in the full code listing that appears at the end of this chapter.
(defmethod frequency ((object note))
"Return the frequency of a note (in Hz.)"
(pitch-to-frequency (pitch object)))
(frequency (note :pitch "C#3")) -> 277.18
Next to being able to retrieve the freqency of a note, it may be necessary to set it to a specified value as well. It is not so difficult to write a procedure that establishes that, called say set- frequency . But now the programmer has to remember that the frequency of a note is changed with a call to the set- frequency procedure, while their pitch has to be updated with an assignment (setf) on the slot accessor. It is clear that this situation is not very elegant. The more so because it may have been the result of a low level implementation decision and, worse, it may be one that has to change in future modifications of the underlying data representation. The uniform way of slot access and method calls in reading slots provides a solution that can be generalized to the writing of slots as well. In the definition of the note class an accessor was given for the pitch slot. This made the system generate a pitch method to read the slot and a method to set the pitch of that slot. The last method is named (setf pitch). This is an extension of the common notion of function names and method names that only allow symbols as names. Upon encountering a (setf (pitch X) Y) the method (setf pitch) is applied to the arguments Y and X. The system supplied the (setf pitch) method that is specialized for notes, because it was asked to do so in the slot descriptor of pitch. The principle of a programmable standard environment[30] applies here as well. And we can define a so called setf method[31] ourselves, specialized for notes. It will be called if in the code a (setf (pitch X) ..) expression, is evaluated where X is a note. This looks just like a slot update.
(defmethod (setf frequency) (value (object note))
"Set the frequency of a note"
(setf (pitch object) (frequency-to-pitch value))
value)
Note the confusing fact that the order in the argument list of the setf method is first the value and then the object: the reverse from the order in which they appear in the call to setf. It is important to let a user-defined setf method return its value, such that we may rely on it to behave the same as ordinary assignments. The auxiliary function frequency- to- pitch is given in the full code listing at the end of this chapter.
[to do: of in een project ergens? ]
Setf methods thus give us the mechanism to solve that problem that we can ask for both the pitch and the frequency of a note but only set the former.
(let ((object (note :pitch "C3")))
(setf (frequency object) 440)
object)
->
(note :duration 1 :pitch "A3")
A rather beautiful consequence of these simple definition of the frequency and (setf frequency) method is the fact that all modification macro's work (like incf and mirrorf) consistently when applied to the frequency of a note, translating the pitch of a note to a frequency, modifying that number in the frequency domain (which is an essentially different operation) and translating the result back to proper pitches. Thus miroring the pitch A1 around the pitch A3 (2 octaves up) give the pitch A5, while miroring the frequency of A1 around the frequency of A3 (a difference of 330 Hz) yields a G4.
(let ((object (note :pitch "A1")))
(format t "~%~S ; ~A Hz" (show object) (round (frequency object)))
(mirrorf (pitch object) "A3") ; 440 Hz
(format t "~%~S ; ~A Hz" (show object) (round (frequency object))))
=>
(note :duration 1 :pitch "A1") ; 110 Hz
(note :duration 1 :pitch "A5") ; 1760 Hz
(let ((object (note :pitch "A1")))
(format t "~%~S ; ~A Hz" (show object) (round (frequency object)))
(mirrorf (frequency object) 440) ; A3
(format t "~%~S ; ~A HZ" (show object) (round (frequency object))))
=>
(note :duration 1 :pitch "A1") ; 110 Hz
(note :duration 1 :pitch "G4") ; 770 Hz
Of course we now want to be able to create a new note of a specified frequency, this can be done in the note constructor.
(defun note (&rest attributes)
"Return a note object with specified attributes (keyword/value pairs)"
(when (getf attributes :frequency)
(setf (getf attributes :pitch)
(frequency-to-pitch (getf attributes :frequency))))
(when (stringp (getf attributes :pitch))
(setf (getf attributes :pitch)
(pitch-name-to-midi-number (getf attributes :pitch))))
(apply #'make-instance 'note attributes))
We will show later how we can modify CLOS' initialization mechanism, to be able to directly supply a new initialization keyword to make- instance.
[to do: create a note from scratch with a specification of its frequency using an initialize instance. simpler maken?, of uitstellen tot intialize-instance :after behandeld wordt? ]
Some calculations on compound musical objects cannot be programmed with the mapc- elements iterator, even though the way in which they visit the parts of a musical object is identical. This is, e.g., the case when side-effects are not appropriate and return values have to be constructed. We will write a simple map- elements which is analogous to the mapc- elements function (it applies an operation to each element of a compound musical object) but this time it collects the results and uses an extra argument that specifies how they are to be combined. In contrast with mapcar, which always combines the results in the list to be returned, this mapper gives some extra flexibility by allowing to specify the method of combination. Supplying list would result in behavior that is like mapcar applied to the elements of a musical object, but other methods of combination (like adding) can be used as well.
(defmethod map-elements ((object compound-musical-object)
combination operation &rest args)
"Combine the results of the operation applied to each element"
(apply combination
(mapcar #'(lambda (element) (apply operation element args))
(elements object))))
We will use this mapper to program the duration method anew.
(defmethod duration ((object sequential))
"Return the duration of a sequential musical object"
(map-elements object #'+ #'duration))
(defmethod duration ((object parallel))
"Return the duration of a parallel musical object"
(map-elements object #'max #'duration))
Which concisely reads that the duration of a sequential structure can be obtained by adding the duration of its elements, and that the duration of a parallel structure is the maximum of the duration of its elements. To further illustrate the mapper's use, we will write a program that counts the number of notes in a musical object.
(defmethod note-count ((object compound-musical-object))
"Return the number of notes in this musical object"
(map-elements object #'+ #'note-count))
(defmethod note-count ((object note))
"Return 1, there is one note in this musical object"
1)
(defmethod note-count ((object pause))
"Return 0, there are no notes in this musical object"
0)
(note-count (example)) -> 4
A slight variation can count the number of musical objects, including compound ones.
(defmethod object-count ((object compound-musical-object))
"Return the number of objects in this musical object"
(1+ (map-elements object
#'+
#'object-count)))
(defmethod object-count ((object basic-musical-object))
"Return one: the multitude of this one objects"
1)
(object-count (example)) -> 6
Another variation counts the number of parallel voices that happen inside a musical object, a function that may come of use when we handle voice allocation for synthesizers with a limited number of oscillators that can generate sound simultaneously.[32]
(defmethod voice-count ((object sequential))
"Return the number of parallel voices in this musical object"
(map-elements object #'max #'voice-count))
(defmethod voice-count ((object parallel))
"Return the number of parallel voices in this musical object"
(map-elements object #'+ #'voice-count))
(defmethod voice-count ((object note))
"Return 1, there is one voice needed for this musical object"
1)
(defmethod voice-count ((object pause))
"Return 0, there are no voices needed for this musical object"
0)
(voice-count (example)) -> 2
Because the duration method is defined for any musical object, it is a simple exercise to define an offset method that calculates when a musical object ends, given its time of onset.
(defmethod offset ((object musical-object) onset)
"Return the end time of a musical object"
(+ onset (duration object)))
Although the appearance of simple expressions which calculate the offset anywhere in the code would not look that incomprehensible, supplying an interface to the data representation of musical objects which is quite rich, and contains, e.g., functions like offset, almost always pays off in unforeseen ways when the data representation has to be extended later. As an example of the use of offset, we define some methods to check whether a musical object is sounding at a specific time, or during a given time interval, given its onset.
(defmethod sounding-at? ((object musical-object) onset time)
"Is the object sounding at time, when started at onset?"
(<= onset time (offset object onset)))
(defmethod sounding-during? ((object musical-object) onset from to)
"Is the object sounding during time-interval [from, to], when started at onset?"
(interval-overlaps? onset (offset object onset) from to))
(defun interval-overlaps? (begin1 end1 begin2 end2)
"Do the intervals [begin,1 end1] and [begin2, end2] overlap?"
(and (<= begin2 end1)
(>= end2 begin1)))
(sounding-during? (note :duration 2) 0 1 3)
->
t
Sometimes transformations need the start time of a note, which is not explicitly stored in the object itself. It is not difficult to define an auxiliary function that calculates the onset times of elements of a compound object, given the onset time of the object itself. Calling this method on a sequential object and its onset time should yield the subsequent onset time of its components, and for a parallel structure will return the list of identical onset times of its components.
(defmethod onsets ((object sequential) &optional (onset 0))
"Return the onsets of the components of object, given its own onset"
(integrate (mapcar #'duration (elements object)) onset))
(defun integrate (durations time)
"Return the running sum of the durations, starting from time"
(when durations
(cons time
(integrate (rest durations) (+ time (first durations))))))
(defmethod onsets ((object parallel) &optional (onset 0))
"Return the onsets of the components of object, given its own onset"
(make-list (length (elements object)) :initial-element onset))
[to do: aansluiting met integrate uit functional maken ]
To test the methods we can apply them to some simple musical objects.
(onsets (sequential (note :duration 1)
(pause :duration 2)
(note :duration 4))
3)
->
(3 4 6)
(onsets (parallel (note :duration 1)
(pause :duration 2)
(note :duration 4))
3)
->
(3 3 3)
Extending the iterator slightly, it can keep track of these onset times and supply them as extra argument to an operation. Just as in mapc- elements all extra arguments supplied are passed on to the operation itself. This often lifts the need for the contruction of a specialized closure for use as operation.[33]
(defmethod mapc-elements-onsets ((object compound-musical-object)
onset
operation
&rest args)
"Apply the operation to each element in a musical object and its onset time"
(loop for element in (elements object)
for element-onset in (onsets object onset)
do (apply operation element element-onset args))
object)
A simple test of this mapper can be undertaken, e.g., by having it print the elements and their onset times of a coumpound object.
(mapc-elements-onsets (sequential (note :duration 1)
(pause :duration 2)
(note :duration 4))
0
#'(lambda (element onset)
(format t "~%~A ; at ~A" (show element) onset)))
=>
(note :duration 1 :pitch "C3") ; at 0
(pause :duration 2) ; at 1
(note :duration 4 :pitch "C3") ; at 3
Using this onsets method for parallel structures as well, allows one definition for the mapc- elements- onsets method for all compound objects (though rather inefficiently defined). We choose here to sacrifice efficiency a bit in favor of the simplicity of the program. A version of mapc- elements- onsets for parallel objects that is more efficient, can always be added.[34] Thus even optimization becomes an activity of adding efficient code for special cases, there is no need to modify existing programs. As such a program will be separated into a part that is essential, elegant, and easy to maintain, and a part that addresses the optimization issues. For now, we will try to extend the elegant part with a drawing program based on this new mapper.
[to do: check volgende plaatjes ]
As an example of the use of mapc- elements- onsets, and to gain an easy way to inspect the results of our transformations, we will write a graphical program to draw a piano-roll notation of a musical structure using this iterator. We will assume that a graphical primitive draw- rectangle exists that draws a rectangle, given a list of the left, top, right and bottom sides. The window on which the pianoroll is drawn is created by the make- piano- roll- window function This window takes care of the drawing of the backdrop of the piano roll (the grid lines and the labels on the axes). [to do: hier een referentie naar een piano-roll project maken ? ]
(defmethod draw (object &rest args)
"Draw a graphical piano-roll representation of a compound musical object"
(let ((window (apply #'make-piano-roll-window args)))
(draw-musical-object object 0 window)
window))
(defmethod draw-musical-object ((object compound-musical-object) onset window)
"Draw a graphical piano-roll representation of a compound musical object"
(mapc-elements-onsets object onset #'draw-musical-object window))
(defmethod draw-musical-object ((object note) onset window)
"Draw a graphical representation of a note (a rectangle)"
(draw-rectangle window (boundary object onset window)))
(defmethod draw-musical-object ((object pause) onset window)
"Draw nothing"
(declare (ignore onset window)))
(defmethod boundary ((object note) onset window)
"Return a list of the sides of a graphical representation of a note"
(declare (ignore window))
(list onset ; left
(+ (pitch object) .5) ; top
(offset object onset) ; right
(- (pitch object) .5))) ; bottom
As you can see, drawing a compound musical object amounts to drawing all its elements at the proper position, drawing a note entails drawing a rectangle. Rests are ignored for the moment. This was in fact the program used to draw Figure ?, Figure ? and Figure ?, as the reader who is using the software that comes with this book can check. Only the grid and the labels on the axes were added. Isn't it surprising how such a simple program can achieve this quite complex task?
In Figure ? the call hierarchy is given for the drawing program. It illustrates which functions (methods) call which others. The mapper itself is left out. The direction of the arrows indicate the "calls" or "invokes" relation, gray arrows mean that the call is made indirectly, through a functional argument that was passed to e.g. a mapper. [to do: tree draw zo maken dat ook grotere cycles getekend kunnen worden, dan kan hier de mapper zelf ook in het diagram ]
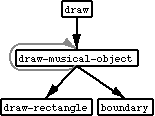
Figure 33. Flow of control in the draw program.
Because mapc- elements- onsets neatly administers the onset time of each musical object it has become easy to define time dependent transformations as well. As example let's program a gradual tempo change, using a general time-time map.[35] The map- time method is given a musical object, its onset and a function from time to time. It calculates new durations by applying this function to the onset and offset times of all basic musical objects, and updates the duration slots accordingly. The make- tempo- change function is given an initial and a final tempo and the duration of the tempo change. It calculates the time-warp function.
(defmethod map-time ((object compound-musical-object) onset time-map)
"Apply a time mapping to the notes of the object"
(mapc-elements-onsets object onset #'map-time time-map))
(defmethod map-time ((object basic-musical-object) onset time-map)
"Adjust the duration of a basic musical object according to the time map"
(let* ((new-onset (funcall time-map onset))
(new-offset (funcall time-map (offset object onset))))
(setf (duration object)(- new-offset new-onset))))
[to do: funtion van score naar perf tijd, dan tempo factoren 1/x. laten we er een mooi sundberg ritard van maken ]
(defun make-tempo-change (duration begin end)
"Return a time-warp function based on begin and end tempo factors"
#'(lambda (time)
(+ (* begin time)
(* (/ (- end begin)
(* 2 duration))
(square time)))))
(defun square (x)
"Return the square of a number"
(* x x))
(draw (map-time (repeat (example) 3 (pause :duration 1))
0
(make-tempo-change 14 1 .33))) =>

Figure 34. A gradual tempo change.
A refinement of our find- element function resembles the way in which mapc- elements was extended into mapc- elements- onsets. It maintains the time of onset and expects the predicate to have at least one extra argument: the onset of the object that it is testing.
(defmethod find-element-onset ((object compound-musical-object)
onset predicate &rest args)
"Return first non-nil predicate's result, testing elements and their onset"
(loop for element in (elements object)
for onset in (onsets object onset)
thereis (apply predicate element onset args)))
(find-element-onset (sequential (note :duration 1 :pitch "C3")
(note :duration 2 :pitch "D#3")
(note :duration 1 :pitch "C#3"))
0
#'(lambda(object onset)(= onset 1)))
->
t
The above example searches through the elements of a sequential musical object and returns t when it encounters an element starting at time 1. Note the use of thereis clause in the body of find- element- onset. This does not just return t when the predicate yields a non-nil value, it returns the value returned by the predicate (just like and, when all its arguments are non-nil, returns the value of its last argument). This enables us to use not-so boolean predicates that return something meaningful, e.g., the object which satified it. In the example below the first note which starts at 0 is returned. This approach makes extra demands to the set of predicates for musical objects, and the ways in which they can be combined. However, it lifts the need for specialized iterators.
(find-element-onset (sequential (note :duration 1 :pitch "C3")
(note :duration 2 :pitch "D#3")
(note :duration 1 :pitch "C#3"))
0
#'(lambda(object onset)
(and (note? object)
(= onset 1)
object)))
->
(note :duration 2 :pitch "D#3")
Recursively calling find- element- onset yields again a refinement of a more general search function that can search through all levels of a musical object using a subtle mutual recursion of find- element and find- musical- object- onset, passing each other through the control structure by way of functional arguments.
(defmethod find-musical-object-onset ((object compound-musical-object)
onset predicate &rest args)
"Return first non-nil predicate's result, testing sub-objects and their onset"
(or (apply predicate object onset args)
(apply #'find-element-onset object onset
#'find-musical-object-onset predicate args)))
(defmethod find-musical-object-onset ((object basic-musical-object)
onset predicate &rest args)
"Return predicate's result, when satisfied for this object at its onset"
(apply predicate object onset args))
To 'read' the code presented above: find- musical- object- onset, first tests the predicate and returns its value when non-nil. When it is nil, and the object under consideration is compound, it calls find-musical-object on itself (passing it aguments as well) to have itself applied to all elements of the object. Note how the use of &rest arguments in the definition of both find- musical- object and find- musical- object- onset allows for the passing of extra parameters that remain invariant. This makes the use of closures to capture the value of those parameters in the functions themselves unneccesary. Note how the predicate itself is shifted in and out of the role of extra argument at the different levels of the recursion: for find- musical- object- onset it is a main parameter, but when passed on to find- element- onset it becomes an extra one, with find- musical- object- onset taking the role of the predicate again. When find- element- onset in turn calls find- musical- object- onset, it passes its extra parameters, with the predicate in the first place, to find- musical- object- onset which thus receives the predicate as a main parameter.
To test our search function we compose a predicate which will return its argument whenever it is applied to a note, its onset, and a time at which the note would be sounding. Because we are composing the sounding- at? predicate of three arguments (the object, its onset and a time) with simple ones of only one argument, we need to wrap those into a function that can be given more arguments, but ignores all abut the first.
[to do: use-only-first-arg-wrap uit functional, of ref naar S K combinators ? ]
(defun use-first-arg (function)
"Wrap the function such that it can be given spurious arguments"
#'(lambda(&rest args)
(funcall function (first args))))
(find-musical-object-onset (example)
0
(compose-and (use-first-arg #'note?)
#'sounding-at?
(use-first-arg #'identity))
3)
->
(note :duration 2 :pitch "D#3")
Please observe that the above search function does not really represent an object oriented style at all: it makes excessive use of functional arguments. It should be kept in mind that the method could have been written in a truely object oriented way with distributed control over the recursion, as we did in the draw- musical- object method. However, the solution presented above is quite elegant and we will use this approach a lot. [36]
Of course our map- elements should be extended to be able to maintain the onset times of the objects to which the operation is applied as well, just like mapc- elements was.
(defmethod map-elements-onsets ((object compound-musical-object)
onset operation &rest args)
"Return the results of the operation applied to each element and its onset"
(loop for element in (elements object)
for element-onset in (onsets object onset)
collect (apply operation element element-onset args)))
To illustrate the use of this iterator, let us write a method that allows us to collect the set of pitches that is being used in a certain time interval in a musical piece. The function to be used when combining the results of the recursive calls on each element of a compound musical object is set- union, which has to be defined by us because Common Lisp only supplies the function to calculate the union of two sets.
(defun set-union (&rest args)
"Return the union of any number of sets"
(reduce #'union args))
(defmethod sounding-pitches ((object compound-musical-object) onset from to)
"Return a list of all pitches that occur in time interval [from, to]"
(apply #'set-union (map-elements-onsets object onset #'sounding-pitches from to)))
(defmethod sounding-pitches ((object note) onset from to)
"Return a list of the pitch of the note, when sounding in interval [from, to]"
(when (sounding-during? object onset from to)
(list (pitch object))))
(defmethod collect-sounding-pitches ((object pause) onset from to)
"Return the empty list representing silence"
nil)
(mapcar #'midi-number-to-pitch-name
(sounding-pitches (example) 0
2 4))
->
("C#3" "D#3" "G2")
To illustrate how behavior defined by means of methods can be extended further, let us modify the piano roll drawing by filling each note rectangle with a dark shade. Here again, we would like to add a piece of code instead of rewriting the draw- musical- object method. In CLOS, methods come in different qualities (we have only used the primary methods unto now). And when more methods are applicable, they are combined by the system using the so called method combination procedures. In our case, the added behavior can operate by side effect, and the extra work can be put in a so called before method or after method. We will assume that a primitive paint- rectangle exists to fill a rectangle with a shade and write a before method for draw- musical- object. The character of this methods is indicated with the method qualifier :before that appears between the name and the argument list.
(defmethod draw-musical-object :before ((object note) onset window)
"Fill a graphical representation of a note with a gray color"
(paint-rectangle window (boundary object onset window) :light-gray))
When a draw- musical- object call is to be executed, the system finds all applicable methods depending on the class of object that the method is applied to and combines them into a whole, the so called effective method. In standard method combination all before and after methods and the primary method are assembled in their proper order. Any behavior that can be conceptualized as a side effect to take place before or after some main behavior that was already defined, can be added in this way. The use of declarative method combination frees the programmer from writing code that searches for methods and calls them in the correct order.
(draw (example)) =>

Figure 35. Shaded piano-roll notation of example.
Note that the source code of the main primary method is not changed - it needs not even be available. Thus also predefined behavior, e.g., of other authors ,or of the Lisp system itself, can be modified or elaborated. The tree diagram in Figure ? depicts where the different draw- musical- object methods are defined, and which will run in the different situations. draw- musical- object has its own definition for a note, a rest and any compound musical object, while one before method exists to do the shading, which is specialized for the class note, and will only run before a note is drawn by its primary method.
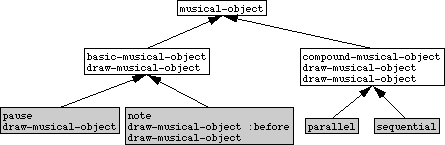
Figure 36. The draw-musical-object method definitions and musical object classes.
[to do: make the methods look different in a different font then the classes (how?) ]
Looking for possible optimization of our code, we see that both draw- musical- object methods for notes call the boundary function, they are repeated below.
(defmethod draw-musical-object :before ((object note) onset window)
"Fill a graphical representation of a note with a gray color"
(paint-rectangle window (boundary object onset window) :light-gray))
(defmethod draw-musical-object ((object note) onset window)
"Draw a graphical representation of a note (a rectangle)"
(draw-rectangle window (boundary object onset window)))
Thus, because the before and the primary method cannot communicate information, the boundary method is wastefully called twice for each note, once in the before method to draw a shaded rectangle, and once in the primary method to draw the boundaries around it. By defining an auxiliary function (draw- boundary), and moving the code that needs the boundary from draw- musical- object (the shared code in both functions) to this new function, this duplicated calculation can be prevented. The draw- boundary embodies thus the action: draw a note given its boundary box.
(defmethod draw-musical-object ((object note) onset window)
"Draw a graphical representation of a note (a rectangle)"
(draw-boundary object (boundary object onset window) window))
(defmethod draw-boundary ((object note) boundary window)
"Draw a box with a specified boundary (left top right bottom)"
(draw-rectangle window boundary))
(defmethod draw-boundary :before ((object note) boundary window)
"Fill a graphical representation of a note with a gray color"
(paint-rectangle window boundary :light-gray))
Before and after methods form a powerfull way to slice-up behaviour in tiny morsels that can be added, managed and grouped much better than bulky code that has to be rewritten for each modification. The possibility to define more methods specialized to the same class with different qualifiers, and in a declarative way state the order in which they must be called, is one of the features that set CLOS aside from many other object oriented languages.
compound-musical-object (musical-object) class
A group of musical objects ordered in time
sequential (compound-musical-object) class
A group of musical objects, one after another
parallel (compound-musical-object) class
A group of musical objects, starting at the same time
note (basic-musical-object) class
A pitched note
basic-musical-object (musical-object) class
A primitive musical object with a duration attribute
pause (basic-musical-object) class
A rest
map-time (object onset time-map) method
Adjust the duration of a basic musical object according to the time map
mapc-elements (object operation &rest args) method
Apply the operation to each element in a musical object
mapc-elements-onsets (object onset operation &rest args) method
Apply the operation to each element in a musical object and its onset time
mirrorf (center) macro
Change a variable by reflecting it around a certain center
map-elements (object combination operation &rest args) method
Combine the results of the operation applied to each element
interval-overlaps? (begin1 end1 begin2 end2) function
Do the intervals [begin,1 end1] and [begin2, end2] overlap?
draw (object &rest args) method
Draw a graphical piano-roll representation of a compound musical object
draw-musical-object (object onset window) method
Draw a graphical representation of a note (a rectangle)
draw-boundary (object boundary window) method
Fill a graphical representation of a note with a gray color
sounding-at? (object onset time) method
Is the object sounding at time, when started at onset?
sounding-during? (object onset from to) method
Is the object sounding during time-interval [from, to], when started at onset?
mirror (object center) method
Mirror all pitches occurring in a musical object around a center
print-object (object stream) method
Prints a description of a musical object as a list to a stream
note-count (object) method
Return 0, there are no notes in this musical object
voice-count (object) method
Return 0, there are no voices needed for this musical object
bar-strict-3/4 nil function
Return a bar of notes in strict 3/4
bar-strict-6/8 nil function
Return a bar of notes in strict 6/8
show (object) function
Return a list describing a musical object with its components or attributes
show-note (object) function
Return a list describing a note object with its attributes
show (object) method
Return a list describing a rest object with its attributes
sounding-pitches (object onset from to) method
Return a list of the pitch of the note, when sounding in interval [from, to]
boundary (object onset window) method
Return a list of the sides of a graphical representation of a note
note (&rest attributes) function
Return a note object with specified attributes (keyword/value pairs)
repeat (object &optional n separator) method
Return a number of repetions of a musical object
parallel (&rest elements) function
Return a parallel musical object consisting of the specified components
pause (&rest attributes) function
Return a rest object with specified attributes (keyword/value pairs)
make-rhythm (durations) function
Return a sequence of notes with given durations
original-and-transform (object separator transform &rest args) method
Return a sequence of the original, a separator, and a transformed object
sequential (&rest elements) function
Return a sequential musical object consisting of the specified components
make-tempo-change (duration begin end) function
Return a time-warp function based on begin and end tempo factors
canon (object n onset-delay) method
Return an n-voiced canon of a musical object
find-element-onset (object onset predicate &rest args) method
Return first non-nil predicate's result, testing elements and their onset
find-musical-object (object predicate &rest args) method
Return object when it satisfies the predicate
object-count (object) method
Return one: the multitude of this one objects
find-musical-object-onset (object onset predicate &rest args) method
Return predicate's result, when satisfied for this object at its onset
duration (object) method
Return the duration of a parallel musical object
collect-sounding-pitches (object onset from to) method
Return the empty list representing silence
offset (object onset) method
Return the end time of a musical object
find-element (object predicate &rest args) method
Return the first element which satifies a predicate, NIL if none do
frequency (object) method
Return the frequency of a note (in Hz.)
note? (object) method
Return the object if it is an instantiation of class note, nil otherwise
pause? (object) method
Return the object if it is an instantiation of class parallel, nil otherwise
sequential? (object) method
Return the object if it is an instantiation of class sequential, nil otherwise
onsets (object &optional onset) method
Return the onsets of the components of object, given its own onset
map-elements-onsets (object onset operation &rest args) method
Return the results of the operation applied to each element and its onset
integrate (durations time) function
Return the running sum of the durations, starting from time
square (x) function
Return the square of a number
set-union (&rest args) function
Return the union of any number of sets
example nil function
Returns a simple structured musical object
(setf frequency) (value object) method
Set the frequency of a note
musical-object nil class
The abstract root class of all musical objects
toss (chance) function
There is a chance that this will return t
pitch-to-frequency (pitch) function
Translate a MIDI number into a frequency (in Hz.)
frequency-to-pitch (frequency) function
Translate a frequency (in Hz.) to a MIDI pitch number
transpose (object interval) method
Transpose all pitches occurring in a musical object over an interval
use-first-arg (function) function
Wrap the function such that it can be given spurious arguments
frere-jacques-canon nil function
frere-jacques-voice nil function
bim-bam-bom nil function
sonner-la-matine nil function
dormez-vous nil function
frere-jacques nil function
copy-object (object) method
strictly-metric-division (duration divisors) function
return a list of strictly metric durations
(Balaban, 1992)
Balaban, M. 1992 Music Structures: Interleaving the Temporal and Hierarchical Aspects in Music. in Balaban, M., K. Ebcioglu & O. Laske (Eds.) Cambridge, Mass.: MIT Press. 111-138
Bamberger (??)
Chowning, 1973 Journal of the Audio Engineering Society, 21(7):526-534. Reprinted inC. Roads and J. Strawn, (Eds.) 1985 Foundations of Computer Music. Cambride, MA: MIT Press. pp. 6-29.
Dannenberg (1993)
Dannenberg, R.B. 1991 Real-time Scheduling and Computer Accompaniment. in Mathews, M.V and J.R. Pierce (Eds.) . Cambridge, MA: MIT Press.
Dannenberg, R.B. 1993 The Implementation of Nyquist, a Sound Synthesis Language. in San Francisco: ICMA.
Dannenberg, R.B., P. Desain and H. Honing (in Press) Programming Language Design for Music. in G. De Poli, A. Picialli, S.T. Pope & C. Roads (Eds.) Lisse: Swets & Zeitlinger.
Desain, P. and H. Honing (In Preparation) CLOSe to the edge, Advanced Object-Oriented Techniques in the Representation of Musical Knowledge. Jounral of New Music Research.
Desain, P. 1990 Lisp as a second language, functional aspects. (28)1 192-222
International MIDI Association 1983 North Holywood: IMA.
Moore, F.R. 1990 Englewood Cliffs, New Jersey: Prentice Hall.
Pope, S.T. 1992 The Interim DynaPiano: An Integrated Computer Tool and Instrument for Composers.16(3) 73-91
Pope, S.T. 1993 Machine Tongues XV: Three Packages for Software Sound Synthesis. 17(2) 23-54
Steele (1990)
Steele (1990, page 791)
Steele, G.R. 1990 Bedford MA: Digital Press.
Tatar,D.G. 1987 Bedford, MA: Digital Press.
abstract class
access function
all functions part of a data abstraction layer (selector and constructor functions). [loaded from Glossary Functional]
accessor function
after method
anonymous function
A function whose 'pure' definition is given, not assigning it a name at the same time. [loaded from Glossary Functional]
applicable method
applicable methods
application
obtaining a result by supplying a function with suitable arguments. [loaded from Glossary Functional]
assignment
atom
in Lisp: any symbol, number or other non-list. [loaded from Glossary Functional]
backwards compatible
before method
class
class hierarchy
class options
combinator
A function that has only functions as arguments and returns a function as result. [loaded from Glossary Functional]
compile time
congruent lambda lists
cons
A Lisp primitive that builds lists. Sometimes used as verb: to add an element to a list. [loaded from Glossary Functional]
constant function
A function that always returns the same value [loaded from Glossary Functional]
constructor function
A function that as part of the data abstraction layer provides a way of building a data structure from its components. [loaded from Glossary Functional]
constructor functions
continuations
A way of specifying what a function should do with its arguments. [loaded from Glossary Functional]
coroutines
parts of the program that run in alternation, but remember their own state of computation in between switches. [loaded from Glossary Functional]
data abstraction
A way of restricting access and hiding detail of data structures [loaded from Glossary Functional]
data abstraction
data type
A class of similar data objects, together with their access functions. [loaded from Glossary Functional]
declaration
declarative
declarative method combination
dialect
A programming language can be split up into dialects that only differ (one hopes) in minor details. Lisp dialects are abundant and may differ a lot from each other even in essential constructs. [loaded from Glossary Functional]
direct superclasses
dynamically typed language
effective method
first class citizens
rule by which any type of object is allowed in any type of programming construct. [loaded from Glossary Functional]
free variables
function
A program or procedure that has no side effects [loaded from Glossary Functional]
function composition
the process of applying one function after another. [loaded from Glossary Functional]
function quote
A construct to capture the correct intended meaning (with respect tothe current lexical environment) of a anonymous function so it can beapplied later in another environment. It is considered good programming style to use function quotes as well when quoting the name of a function. [loaded from Glossary Functional]
functional abstraction (or procedural abstraction)
A way of making a piece of code more general by turning part of it into a parameter, creating a function that can be called with a variety of values for this parameter. [loaded from Glossary Functional]
functional argument (funarg)
A function that is passed as argument to another one (downward funarg) or returned as result from other one (upward funarg) [loaded from Glossary Functional]
generalizedvariable
generic
global variables
an object that can be referred to (inspected, changed) from any part of the program. [loaded from Glossary Functional]
higher order function
A function that has functions as arguments. [loaded from Glossary Functional]
imperative style
inheritance
initializationkeyword
initializationprotocol
initialization argument list
initialization keyword
instance
instantiation
iteration
repeating a certain segment of the program. [loaded from Glossary Functional]
lambda list keyword
lambda-list keyword
A keyword that may occur in the list of parameter names in a function definition. It signals how this function expects its parameters to be passed, if they may be ommited in the call etc. [loaded from Glossary Functional]
lexical scoping
A rule that limits the 'visibility' of a variable to a textual chunk of the program. Much confusion can result from the older- so called dynamic scoping - rules. [loaded from Glossary Functional]
list
message passing
meta object protocol
method
method combination
The declaritive way in which CLOS allows more methods to be bundled and run, in situations where more are applicable
method qualifier
methods
modification macro's
most specific method
multi-methods
multiple inheritance
name clash
name clashes
object oriented programming
A style of programming whereby each data type is grouped with its own access function definitions, possibly inheriting them from other types. [loaded from Glossary Functional]
object-oriented style
parameter-free programming
A style of programming whereby only combinators are used to build complex functions from simple ones. [loaded from Glossary Functional]
part-of hierarchy
polymorphic
polymorphism
prefix notation
A way of notating function application by prefixing the arguments with the function. [loaded from Glossary Functional]
primary method
primary methods
procedural
quote
A construct to prevent the Lisp interpreter from evaluating an expression. [loaded from Glossary Functional]
read-eval-print
record
recursion
A method by which a function is allowed to use its own definition. [loaded from Glossary Functional]
run time
selector function
A function that as part of the data abstraction layer provides access to a data structure by returning part of it. [loaded from Glossary Functional]
selector functions
setf method
shadow
side effect
side effect
Any actions of a program that may change the environment and so change the behavior of other programs. [loaded from Glossary Functional]
slot descriptors
slots
stack
A list of function calls that are initiated but have not yet returned a value. [loaded from Glossary Functional]
standard method combination
statically typed
structure preserving
A way of modifying data that keeps the internal construction intact but may change attributes attached to the structure. [loaded from Glossary Functional]
tail recursion
A way of recursion in which the recursive call is the 'last' thing the program does. [loaded from Glossary Functional]
untyped language
make the methods look different in a different font then the classes (how?)
use-only-first-arg-wrap uit functional, of ref naar S K combinators ?
funtion van score naar perf tijd, dan tempo factoren 1/x. laten we er een mooi sundberg ritard van maken
tree draw zo maken dat ook grotere cycles getekend kunnen worden, dan kan hierde mapper zelf ook in het diagram
hier een referentie naar een piano-roll project maken ?
check volgende plaatjes
aansluiting met integrate uit functional maken
create a note from scratch with a specification of its frequency using an initialize instance.simpler maken?, of uitstellen tot intialize-instance :after behandeld wordt?
of in een project ergens?
Hier een keer een score generen met 6/8 indicatie en beaming en vast weergeven (:eval? nil) met de aanroep (play (bar-strict-6/8))
beter snappen waarom tree draw niet precies goed de sizes uitrekent, is nu een truc
could go somewhere else to enlighthen, when needed: gebruikt geen OO of afhankelijkheden
tekst en noten checken
verwijzing naar meta-object-auto-type-prediactes in de voetnoot zetten
This topic is elaborated further in ??
als er een soort non-destructive modify/substitute is, uit vorig hoofdstuk, op property lists dan die gebruilken
make this chapter
waar is deze pict gebleven?
read macros for note syntax, load forms
Make a picture of keyboard +pitchnames + midi numbers) add ref in footnote
grapje over klasse bewustzijn, engelsen of marx
meer voorlezen van code bv defclass form
:WARNING, : RULE-OF-THUMB, :SOUNDBYTES styles
use of ":" just before code example.
use of e.g. in text (forexample, for instance intext, e.g., tussen haakjes)e.g. - e.g., of , e.g.,
In intro OOI zowel MIDI keynumbers uitgelegd als primitive keuze "on basis of esthetic or pragmeatic grounds" genoemd
[an error occurred while processing this directive]