
[an error occurred while processing this directive]
Draft mars 11, 1997
- Lists as the main data structure
- Abstraction and application as dual mechanisms
- Conditionals as control structure
- Recursion as main control structure
- Binding as a way to retain intermediate results
- Functions as first class objects
- Functions as arguments
- Functions as results
- Generality as aim
- Combinators as function builders
- More on generality as aim
- Parameters as superfluous
- Definitions made
- Literature references made
- Glossary references made
- Text references made
This chapter introduces the functional style of programming with lists as the sole data structure and recursion as the main control structure. It will present the basics of Lisp in the form of examples that you will find reused throughout the book.
The primary data type of Lisp is the list. It is notated as an open parenthesis followed by zero, or more elements, and a closing parenthesis. To give an example, the following list could be used as a representation for a note that has a duration of 2 time-units, a pitch of C (MIDI [1] key number 60) and maximum loudness:
(note 2 60 1)
Consider the choice of this primitive musical object here as an arbitrary one, we just need one such object in our examples. We will see that the choice of primitives is a very important one, based on esthetic grounds -it expresses your idea of the atomic musical object and its parameters- and on pragmatic grounds -it will determine which operations can be expressed easily and elegantly, and which are more difficult to express or even impossible.
There is one special list, the empty list, notated as () or nil. The elements of a list can be symbols, called atoms, (like note or 60) or they can be lists. Thus a collection of notes can be represented as a list of lists:
((note 1 60 1)(note 2 61 0.7)(note 1 55 1))
If we wish to express control over the timing structure in the representation, ordering a collection of notes, we could form sequential and parallel structures. This way of specifying the time relations between objects is an alternative to the use of absolute start times found in most composition systems. It makes explicit the time-relation between its elements. Sequential indicates that its elements are in succeeding order, one after the other (like notes in a melody), parallel indicates that its elements are simultanuous (like in a chord). The first example shows a sequential object, the second a nesting of a parallel and sequential object. As such we can construct more elaborated structured or compound musical objects.
(sequential (note 1 60 1)(note 2 61 0.7))
(parallel (sequential (note 1 60 1)
(note 2 63 1))
(note 4 55 0.5))
A piano-roll notation of the second musical object is given in Figure 1. Figure 2 visualises its tree structure as a part-of hierarchy: parallel, at the top, has two parts (a sequential structure and a note) and sequential, in turn, has two notes as parts.

Figure 1. Piano-roll notation of the example.
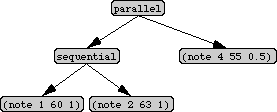
Figure 2. Example data structure.
Note that the words like note, sequential and parallel do not have any intrinsic meaning here, since they are not being build-in Lisp functions. They are just used as arbitrary symbols, signalling our intention with the data in that list. In Common Lisp there are of course other data types available like strings, arrays, hash tables, etc. which sometimes are more appropriate then lists. They will be discussed in later chapters, here we will restrict ourselves to lists.
The very heart of any functional programming language consists of a pair of dual constructs, the first of which is called application. It is the action of 'calling' a function on one or more arguments. The syntactical form of an application is the name of the function followed by its arguments, together enclosed by parentheses (prefix notation). In the example below the function + is applied to the arguments 1 and 3. The arrow (->) points to the result of the evaluation of an expression.
(+ 1 3) -> 4
(first '(note 1 60 1)) -> note
The second expression applies the function first to one of our note objects. Note that the list is preceded by a quote ('). In this way we make it a constant data list. It prevents the Lisp interpreter from recognizing (note 1 60 1) as an application of a function note to the arguments 1, 60 and 1. The result of evaluating the expression is the atom note.
There are two selector functions that take lists apart: first and rest.[2] There is one constructor function for building lists, called cons. Below some examples using these functions.
(rest '(note 1 60 1)) -> (1 60 1)
(first (rest '(note 1 60 1))) -> 1
(cons 'note '(1 60 1)) -> (note 1 60 1)
Note that in these examples atoms, like note, have to be quoted (to prevent them from being interpreted as a variable, something we will discuss shortly). Numbers are always constant and do not need to be quoted.
There are more Lisp primitives available for the construction of lists (e.g., append that concatenates several lists and list which builds a list out of several elements at once). However, they can all be written by the programmer using only cons. Below three ways of constructing the same note data structure:
(append '(note 1) '(60 1)) -> (note 1 60 1)
(list 'note 1 60 1) -> (note 1 60 1)
(cons 'note (cons 1 (cons 60 (cons 1 nil)))) -> (note 1 60 1)
Application should be used as the only means to pass information to a function. This ensures that the behavior of functions is not dependant upon the context of its call. In other words, the result of applying a function is only dependent on the value of its the argument: it is garanteed to give the same result, independent of where in the program code this function was evoked. This is a very central and useful notion in functional programming.[3]
The second central notion is called functional abstraction and transforms an expression (a piece of program text) into a function. This can be done with the lisp construct defun. Defun is a special form, which means that it uses a non-standard indiosyncratic syntax consisting of the name of the function, a list of zero or more arguments, a documentation string describing the function (text enclosed by double quotes (")), and the body of the function. The function below is a constant function named example without arguments that will just return, as a result, a simple constant musical structure. We will use this function a lot in the next paragraphs:
(defun example ()
"Return a constant musical object"
'(sequential
(parallel (note 1 60 1)
(note 2 63 1))
(note 4 55 0.5)))
(example) ->
(sequential (parallel (note 1 60 1)
(note 2 63 1))
(note 4 55 0.5))
(draw (example)) =>
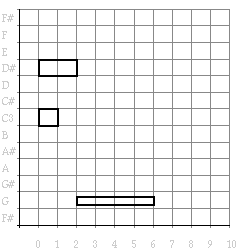
Figure 3. The pianoroll representation of the example.
We will use the function draw to generate graphical piano-roll representation[4] of our examples, a function you will be able to write yourself somewhat later in this chapter.
The documentation string that we add to all our functions is always be accessible, and can be obtained from all lisp functions. The function documentation takes the name of a function and its type (in this chapter always a function), and returns the documentation string describing it.
(documentation 'list 'function) ->
"Return a list containing arguments as its elements."
The documentation string of our newly defined function example is accessible as well:
(documentation 'example 'function) ->
"Return a constant musical object"
Documentation strings can form the basis of simple tools for documentation or for sophisticated auto documenting programs, as we will see later. For now, we will move on and define a number of functions that have one argument and select a specific element out of a list.[5]
In the first example below a function called second- element is defined which has one parameter called list. In the definition the parameter list is said to be abstracted from the body. Only when second- element is applied to an actual argument does the body becomes 'concrete' in the sense that it 'knows' what the parameter list stands for, so that its value can be calculated. Its body is the application of the functions first and rest to this parameter.
(defun second-element (list)
"Return second element of list"
(first (rest list)))
(defun third-element (list)
"Return third element of list"
(first (rest (rest list))))
(defun fourth-element (list)
"Return fourth element of list"
(first (rest (rest (rest list)))))
(second-element '(c d e f g a b)) -> d
(third-element '(c d e f g a b)) -> e
(fourth-element '(c d e f g a b)) -> f
A data structure always is accompagnied by functions that can access them, so-called selector functions, and a function that can make a new one, named a constructor function. Together they are referred to as a data abstraction layer, since the use (acessing and making them) and the actual form of the data (a list in our case) are clearly separated. When changing the data type (e.g., to an array) we only have to change this set of functions without affecting the workings of our other programs. We will now describe a constructor function and some selector functions for our musical object note making use of our list access functions defined above.
(defun make-note (duration pitch loudness)
"Return a note data structure"
(list 'note duration pitch loudness))
(defun duration (note)
"Return the duration of note"
(second-element note))
(defun pitch (note)
"Return the pitch of note"
(third-element note))
(defun loudness (note)
"Return the amplitude of note"
(fourth-element note))
(duration '(note 3 60 1)) -> 3
(pitch '(note 3 60 1)) -> 60
(make-note 3 60 1) -> (note 3 60 1)
In the same way we could program a set of selector and constructor functions as a data abstraction layer for sequential and parallel structures.
(defun make-sequential (musical-object-1 musical-object-2)
"Return a sequential data structure"
(list 'sequential musical-object-1 musical-object-2))
(defun make-parallel (musical-object-1 musical-object-2)
"Return a parallel data structure"
(list 'parallel musical-object-1 musical-object-2))
(defun first-structure-of (musical-object)
"Return the first element of a musical object"
(second-element musical-object))
(defun second-structure-of (complex-structure)
"Return the second element of a musical object"
(third-element complex-structure))
(defun structural-type-of (musical-object)
"Return a type of a musical object"
(first musical-object))
(structural-type-of (example)) -> sequential
(second-structure-of (example)) -> (note 4 55 0.5)
This is a good moment to play around with these expressions in your Lisp interpreter, and get aquainted with the mechanism of evaluating Lisp expressions and defining functions (if you not already did this!).
It is not always desired to pass values for all arguments of a function, for instance, when default values would be good enough. For this Common Lisp provides control in the form of lambda-list keywords. Optional parameters to a function (that will be assigned a default value when missing in the function call) can be defined by means of the &optional lambda-list keyword, followed by one or more lists each containing an argument name and its default value.[6]Below we redefine our constructor make- note using optional parameters.
(defun make-note (&optional (duration 1) (pitch 60) (loudness 1))
"Return a note data structure"
(list 'note duration pitch loudness))
(make-note 2 61) -> (note 2 61 1)
(make-note) -> (note 1 60 1)
Another useful lambda-list keyword is &rest. It is followed by one parameter that collects all the arguments of the function is a list;
(defun make-note (&rest args)
"Return a note data structure"
(cons 'note args))
(make-note 2 61 1) -> (note 2 61 1)
A third lambda-list keyword is &key, [7] with which the order in which the arguments have to be passed to a function is not fixed anymore. The syntax is the same as the optional keyword: one or more lists containing the argument name and its default value. When calling such a function, every argument has to be preceded by a keyword indicating for which parameter the value following it is intended. Below another rewrite of the function make- note using keywords, one that we will stick to for a while.
(defun make-note (&key (duration 1) (pitch 60) (loudness 1))
"Return a note data structure"
(list 'note duration pitch loudness))
(make-note :duration 2 :pitch 61) -> (note 2 61 1)
(make-note :pitch 62 :duration 2) -> (note 2 62 1)
Combinations of different lambda-list keywords can generate some confusion. For the time being, a good rule is to use only one at a time in a function definition.
We now can use these new definitions to construct some useful note transformations:
;;; utility functions
(defun clip (min value max)
"Return the value, clipped within [min,max]"
(cond ((< value min) min)
((> value max) max)
(t value)))
(defun transpose-pitch (pitch interval)
"Return pitch increased by interval"
(+ pitch interval))
(defun mirror-pitch (pitch center)
"Return pitch mirrored around center"
(- center (- pitch center)))
;;; general note transforms
(defun transpose-note (note interval)
"Return note transposed by interval"
(make-note :duration (duration note)
:pitch (transpose-pitch (pitch note) interval)
:loudness (loudness note)))
(defun limit-loudness (note low high)
"Return note with clipped loudness"
(make-note :duration (duration note)
:pitch (pitch note)
:loudness (clip low (loudness note) high)))
(defun mirror-note (note center)
"Return note mirrored around center"
(make-note :duration (duration note)
:pitch (mirror-pitch (pitch note) center)
:loudness (loudness note)))
;;; dedicated note transforms
(defun transpose-note-semitone (note)
"Return note transposed by semi-tone"
(transpose-note note 1))
(defun mirror-note-around-middle-c (note)
"Return note mirrored around middle-c"
(mirror-note note 60))
(limit-loudness '(note 1 57 .2) 0.5 1) -> (note 1 57 0.5)
(transpose-note-semitone '(note 1 60 1)) -> (note 1 61 1)
(mirror-note-around-middle-c '(note 1 57 1)) -> (note 1 63 1)
Since this is a larger code fragment, we use comments to visually group portions of the code. Comments are text preceeded by a ; (a semicolon). The semicolon and all text following it until the next line, are ignored by the Lisp reader. It is considered good style to use three semicolons to indicate larger code blocks, two semicolons to preceed information about the code section following it, and one semicolon to add information about the code it is next to. Note that this is all convention, since one semicolon would be enough.[8]
In the large code fragment above we first defined some utility functions, then some general note transforming functions, to finally use these to define the dedicated ones that will be used in the coming examples. The utility functions for the pitch arithmetic isolate the calculation of pitches from the note transforming functions. This process of deciding for the abstraction layers is one of the essential aspects of programming style - something that is not demanded by the programming language itself but solely dependent on the taste and good judgement of the programmer.
With conditionals you can write functions that will, depending the value of one or more tests, evaluate a particular lisp expression. As an example take the function maximum.
(defun minimum (a b)
"Return minimum value of a and b"
(if (< a b)
a
b))
(minimum 6 4) -> 4
It takes two numbers as argument and returns the number with the smallest value. The function < (less-then) is a predicate, a function that returns a truth value, True or False (t or nil in Lisp). Furthermore, we use the special form if. It has as special syntax a test-form (here (< a b)) and two lisp expressions (here a and b respectively), the first one (the then-form) is evaluated and returned when the test-form is true, the second (the else-form) is evaluated and returned when it is false.
In Lisp the empty list () and the truth value False are defined equivalent and called nil. Conversly, everything that is not nil is considered as True: t. Other useful predicates are:
(equalp '(note 1 57 1) '(note 1 57 1)) -> t
(= 6 4) -> nil
(listp '(note 1 60 1)) -> t
(null '(note 1 60 1)) -> nil
The predicate equalp is the most general test for equality, = is specially for testing equality of numbers (although equalp would do as well)[9], listp tests whether its argument is a list, and null tests whether its argument is the empty list. [10]
Logical operators (and, or and not) are often useful in combining predicates.
(defun same-note? (note-1 note-2)
"Return true when notes are equal, false otherwise"
(and (= (duration note-1) (duration note-2))
(= (pitch note-1) (pitch note-2))
(= (loudness note-1) (loudness note-2))))
(defun note? (object)
"Return true if note, false otherwise"
(and (listp object)
(equalp (structural-type-of object) 'note)))
(same-note? '(note 1 61 1) '(note 1 61 0.7)) -> nil
(note? '(note 1 61 1)) -> t
There are different conditional constructs in Lisp. However, they can all be written in terms of the if construct. Take, for instance, the next two predicate functions using if:
(defun middle-c? (note)
"Return true if pitch of note is 60, false otherwise"
(if (= (pitch note) 60)
note
nil))
(defun sounding-note? (note)
"Return true if amplitude of note is non-zero, false otherwise"
(if (= (loudness note) 0)
nil
note))
(middle-c? '(note 1 61 1)) -> nil
(sounding-note? '(note 1 60 1)) -> (note 1 60 1)
Sometimes, to make the code more readable, one of the alternative conditionals are applicable. The two functions above, for example, can be written in a simpler form. When in an if there is no else-form, when should be used:
(defun middle-c? (note)
"Return true if pitch of note is 60, false otherwise"
(when (= (pitch note) 60) note))
When there is no then-form, unless should be used:
(defun sounding-note? (note)
"Return true if amplitude of note is non-zero, false otherwise"
(unless (= (loudness note) 0) note))
The body of sounding- note? could also have been written as (when (not (= (loudness note) 0)) note), but this is considered less readable.
For more complicated conditionals we will use the more general construct cond. This construct has an elaborate syntax consisting of one or more clauses, each clause consisting of a test-form and one or more then-forms of which the last form is returned as result. Below, first a version using if is shown, followed by a more readable version using cond.
(defun amplitude-to-dynamic-marking (value)
"Return a dynamic marking associated with an amplitude value"
(if (< 0.8 value)
'ff
(if (< 0.6 value)
'f
(if (< 0.4 value)
'mp
(if (< 0.2 value)
'p
'pp)))))
(defun amplitude-to-dynamic-marking (value)
"Return a dynamic marking associated with an amplitude value"
(cond ((< 0.8 value) 'ff)
((< 0.6 value) 'f)
((< 0.4 value) 'mp)
((< 0.2 value) 'p)
(t 'pp)))
In the cond construct the test-form of the last clause, by convention, is always T. It contains the code for the situation not covered by any of the other test-forms.[11] In the following function calls an amplitude value 0.66 is converted to the dynamic marking fortissimo, and the value 0.1 to pianissimo.
(amplitude-to-dynamic-marking 0.66) -> f
(amplitude-to-dynamic-marking 0.1) -> pp
The order of the clauses in a cond construct is important. Note that we actually use the order in which the test-forms are evaluated (i.e. starting from the top), using the knowledge that a certain test is only evaluated when previous tests have been false. In the function amplitude- to- dynamic- marking above using cond it is used to code that values between, for example, 0.6 and 0.8 are converted into F, by only testing whether the value is bigger than 0.6. In some situations (e.g., with more complex tests) it is wiser to make this explicit, as shown in the next example. The predicate between? is introduced to abstract from the notion of a range:
(defun between? (value min max)
"Return true when value in interval <min, max], false otherwise"
(and (< min value) (<= value max)))
(defun amplitude-to-dynamic-marking (value)
"Return a dynamic marking associated with an amplitude value"
(cond ((between? value 0.8 1.0) 'ff)
((between? value 0.6 0.8) 'f)
((between? value 0.4 0.6) 'mp)
((between? value 0.2 0.4) 'p)
(t 'pp)))
The predicate <= tests whether its first argument is less than or equal to its second argument.[12]
We can also write the function that converts dynmamic markings to amplitudes using a cond. When the argument mark has none one of the values tested in the clauses, it will return 0.1.13
(defun dynamic-marking-to-amplitude (mark)
"Return an amplitude value associated with a dynamic marking"
(cond ((equalp mark 'ff) 0.9)
((equalp mark 'f) 0.7)
((equalp mark 'mp) 0.5)
((equalp mark 'p) 0.3)
(t 0.1)))
(dynamic-marking-to-amplitude 'mp) -> 0.5
It is in these situations, where one form is tested to have different values the case contruct is appropiate. In the next example, the value of the argument is used as a key to select the appropiate amplitude associated with a dynamic mark:
(defun dynamic-marking-to-amplitude (mark)
"Return an amplitude value associated with a dynamic marking"
(case mark
(ff 0.9)
(f 0.7)
(mp 0.5)
(p 0.3)
(otherwise 0.1)))
The case contruct will evaluate its first argument (the key-form), then select a subsequent clause starting with that value (the key), followed by an evaluation the second part of that clause. The final case is preceded by otherwise, and contains the form to be evaluated when none of the other cases apply (like the t clause in cond construct).
Recursion provides an elegant way of reducing complex problems into simpler ones. This is done by first defining the solution to a simpler problem then recursively applying this solution (a piece of program code) to a more complex problem. A recursive function definition often has a characteristic pattern: a conditional expression, consisting of a stop-condition (or bottoming-out condition) for detecting the terminating non-recursive case of the problem, the result in that case (the stop-result), and the construction of a simpler, or reduced version of the overall problem by means of a recursive call. Below a template of a recursive function is shown. The aspects that still have to be filled in, dependent on the specific problem at hand, are bracketed with <>.
(defun <function name> <argument list>
(if <stop-condition>
<stop-result>
<recursive construction>))
As a first example, take the transposition of a collection, i.e. a list of notes.
(defun transpose-note-list-semitone (notes)
"Return a list of notes transposed by a semitone"
(if (null notes)
nil
(cons (transpose-note-semitone (first notes))
(transpose-note-list-semitone (rest notes)))))
When the list is empty (i.e. (null notes) is true) the task is simple: nothing has to be done. Otherwise we put (i.e. cons) the transposition of the first note in the result of transposing the rest of the list. Maybe surpisingly, the function required for transposing this smaller list is precisely the function we are writing at this moment, so it only has to call itself. This process of self-reference is called recursion. To improve readability, we could make the test-form of the if positive by replacing (null notes) by notes, i.e. testing whether there are notes, instead of testing the situation of no notes left:
(defun transpose-note-list-semitone (notes)
"Return a list of notes transposed by a semitone"
(if notes
(cons (transpose-note-semitone (first notes))
(transpose-note-list-semitone (rest notes)))
nil))
And, since the else-form is nil, we should use a when conditional:
(defun transpose-note-list-semitone (notes)
"Return a list of notes transposed by a semitone"
(when notes
(cons (transpose-note-semitone (first notes))
(transpose-note-list-semitone (rest notes)))))
In this final rewrite, the when condition tests whether there are any notes left. If so, it transposes the first one and puts it in the already transposed rest of the note list. If not, the result of the when clause will be nil, and this will be the empty starting list for consing in transposed notes.
(transpose-note-list-semitone
'((note 1 60 1)(note 2 59 0.7)(note 1 65 0.7))) ->
((note 1 61 1)(note 2 60 0.7)(note 1 66 0.7))
Another example of a list recursive function is integrate. It can be used to convert a list of durations into a list of onsets by adding (starting from offset) the successive durations:
(defun integrate (numbers &optional (offset 0))
"Return a list of integrated numbers, starting from offset"
(if (null numbers)
(list offset)
(cons offset
(integrate (rest numbers)
(+ offset (first numbers))))))
(integrate '(1 2 3) 0) -> (0 1 3 6)
The function integrate uses the standard stop-condition for list recursion and constructs recursively a list of onsets by adding in every recursive call a duration to the current value of offset
Both transpose- note- list- semitone and integrate are examples of example of list recursion. They recur over a list, element by element, have a stop-condition that tests on lists and a recursive call where a new list is constructed. Another example of list recursion is shown in the next example:
(defun nth-element (n list)
"Return n-th element of list (zero-based)"
(cond ((null list)
nil)
((= n 0)
(first list))
(t (nth-element (- n 1) (rest list)))))
(nth-element 0 '(pp p mp f ff)) -> pp
(nth-element 2 '(pp p mp f ff)) -> mp
It is constructed using a slightly adapted recursive template, with an extra test added:
(defun <function name> <argument list>
(cond (<stop-condition>
<stop-result>)
(<specific-test>
<specific result>)
(t <recursive call>))
This extra test tests whether n is zero, and if so, returns the first elements of the list. In the final clause the function nth- element is called recursively with a decremented n and the rest of the list. Note that there is no new list constructed here. [14] We could use this function to rewrite, once again, amplitude- to- dynamic- marking:
(defun amplitude-to-dynamic-marking (value)
"Return a dynamic marking associated with an amplitude value"
(nth-element (round (* value 5)) '(pp p mp f ff)))
(amplitude-to-dynamic-marking .3) -> mp
While newly designed languages accepted recursion as control structure, Lisp was augmented with 'down-to-earth' and well-known iterative control structures, since it was recognized that in some cases it is simpler for humans to use instead of recursion (See chapter nil: imperative style). For complex cases however, the recursive form is often more elegant and easier to read. For example, if we wish to define a transposition on a complex musical structure (built from parallel and sequential), we must first dispatch on the type of structure (using a case construct) and then apply the transformation recursively on the component structures, to finally reassemble the transposed parts into their parallel or sequential order. The resultant program would look very messy when written iteratively. In general it can be said that recursion is the natural control structure for hierarchical data. And hierarchical structures are common in music.
(defun transpose-semitone (musical-object)
"Return a musical object transposed by a semitone"
(case (structural-type-of musical-object)
(note (transpose-note-semitone musical-object))
(sequential (make-sequential
(transpose-semitone (first-structure-of musical-object))
(transpose-semitone (second-structure-of musical-object))))
(parallel (make-parallel
(transpose-semitone (first-structure-of musical-object))
(transpose-semitone (second-structure-of musical-object))))))
(transpose-semitone (example)) ->
(sequential (parallel (note 1 61 1)
(note 2 64 1))
(note 4 56 0.5))
For numeric recursion we need to think of the appropiate the stop-condition and the recursive construction.
(defun <function name> <argument list>
(if <stop-condition>
<stop-result>
<recursive construction>))
The stop-condition will be a test on a number and the recursive construction will have to make new numbers (e.g., by multiplying them).
(defun exponent (number power)
"Return number raised to power"
(if (= power 0)
1
(* number (exponent number (- power 1)))))
(exponent 2 2) -> 4
The simplest case for exponent is a number raised to the power 0, which is 1. This is the stop condition in the function. Otherwise we multiply number by the result of exponent applied to number and the power decremented by one. We could use this function to convert from MIDI pitches to frequencies:[15]
(defun semitone-factor ()
"Return a constant factor"
1.0594630943592953)
(defun pitch-to-frequency (pitch)
"Translate a MIDI number into a frequency (in Hz.)"
(* 440.0 (exponent (semitone-factor) (- pitch 58))))
(pitch-to-frequency 70) -> 880.0
Finally, we return to list recursion with the function retrogarde, that reverses the elements in a list. We do this by puting the first note of the list at the end of the rest of the list, assuming that the rest is already reversed: we apply the function we are writing to it:
(defun retrogarde (notes)
"Return a reversed note list"
(when notes
(append (retrogarde (rest notes))
(list (first notes)))))
(retrogarde '((note 1 61 1)(note 2 64 1)(note 4 56 0.7))) ->
((note 4 56 0.7) (note 2 64 1) (note 1 61 1))
A more efficient way of coding this function is to use an accumulating parameter; instead of having to administrate all recursive calls to retrogarde, before being able to append one item to it, we can write the following[16]:
(defun retrogarde (notes)
"Return a reversed note list"
(accumulating-retrogarde notes nil))
(defun accumulating-retrogarde (notes result)
"Return a reversed note list, an auxiliary function"
(if (null notes)
result
(accumulating-retrogarde (rest notes)
(cons (first notes) result))))
This can be reduced to one function when we use an &optional argument. Note that result after the &optional is short for (result nil).
(defun retrogarde (notes &optional result)
"Return a reversed note list"
(if (null notes)
result
(retrogarde (rest notes)
(cons (first notes) result))))
Initially, retrogarde is called with result being nil. [17] This parameter is then recursively filled with the elements of the note list and, when notes is empty, returned. The list will have all the notes in a reverse order because we put the first one in first, the second before that, etc.
In some situations, however, a simple list iterator would be enough. For instance, the function mapcar that applies a function to each item of a list and returns the individual results in a list. This function is useful for structures that have no hierarchy. For example, a flat list of notes like in the example below:
(mapcar #'pitch '((note 1 60 1)(note 1 62 1)(note 1 63 1))) -> (60 62 63)
[to do: ongeveer hier iets over een car/cdr recursie? En, symmetrisch, mapcar fun op elements and sub-elements, transpose uitschrijven? ]
In larger fragments of code it is often useful to temporary bind results that are used further on in the code. There are a number of binding constructs in Common Lisp that can be used for this The most common one is let, a special form, that thus comes with its own special syntax. It takes a list of variable bindings and then the code that can refer to these. The bindings are pairs of variable names and their values. In the following example the note (note 1 60 1) is bound to the variable name note- a, and (note 2 62 .5) to note- b. In the body these two values are combined into a sequential structure. They can be refered to everywhere in the body of the let. However, outside the let they do not exist. This is called lexical scope: these variables can only be refered to within the establishing construct in which they are textually contained.
(let ((note-a '(note 1 60 1))
(note-b '(note 2 62 .5)))
(make-sequential note-a note-b)) ->
(sequential (note 1 60 1) (note 2 62 .5))
In a let all variables are calculated in parallel (i.e. first all values are calculated and then binded to variable names). When we want to use a variable-name in the description of a succeeding variable, we can use let*, that binds names sequentially:
(let* ((note-a '(note 1 60 1))
(note-b (make-note :duration 2
:pitch (pitch note-a)
:loudness .5)))
(make-sequential note-a note-b)) ->
(sequential (note 1 60 1) (note 2 60 .5))
Another useful binding construct is destructuring- bind. The first argument is a list with variable names. They are bound to the respective elements of the list that results from evaluating the expression, the second argument. Then the body of code follows, just like let.
(destructuring-bind (type note-a note-b)
'(sequential (note 1 60 1) (note 2 60 .5))
(make-sequential note-b note-a)) ->
(sequential (note 2 60 0.5) (note 1 60 1))
In fact, this is short-hand for writing:
(let* ((object '(sequential (note 1 60 1) (note 2 60 .5)))
(type (first object))
(note-a (second object))
(note-b (third object)))
(make-sequential note-b note-a))
destructuring- bind is especially useful when there are no accessors for the destructured data structure.
In any good programming language all possible objects are allowed to appear in all possible constructs: they are all first class citizens. However in many programming languages this rule is often violated. In Lisp even exotic objects such as functions can be passed as an argument to a function (in an application construct) or yielded as a result from a function. At first sight this may seem unusual. PASCAL, for example allows the name of a procedure to be passed to another one using an ad hoc construction. And in C pointers to functions can be passed around. However, in Lisp all functions are uniformly considered as data objects in their own right, and functions operating on these them can be used. This provides an abstraction level that is a real necessity, but that is so often lacking in many other languages.
Suppose we want to write a function mirror- around- middle- c which would look similar to transpose- semitone defined before but only uses mirror- note- around- middle- c instead of transpose- note- semitone as the note transformation:
(defun mirror-around-middle-c (musical-object)
"Return a musical object mirror around middle c"
(case (structural-type-of musical-object)
(note (mirror-note-around-middle-c musical-object))
(sequential (make-sequential
(mirror-around-middle-c (first-structure-of musical-object))
(mirror-around-middle-c (second-structure-of musical-object))))
(parallel (make-parallel
(mirror-around-middle-c (first-structure-of musical-object))
(mirror-around-middle-c (second-structure-of musical-object))))))
Instead of just writing a new function for that purpose, it is better to abstract from the note transformation and write a general transform function. This function is now given the note transformation as an extra functional argument, which enables it to deal with all kinds of note transformations. Wherever it needs the result of the application of the note transformation function to a specific note. This is calculated with the Lisp funcall construct, that applies the value of its first argument (a function) to zero or more arguments:
(defun transform (musical-object note-transform)
"Return a transformed musical object"
(case (structural-type-of musical-object)
(note
(funcall note-transform musical-object))
(sequential
(make-sequential (transform (first-structure-of musical-object)
note-transform)
(transform (second-structure-of musical-object)
note-transform)))
(parallel
(make-parallel (transform (first-structure-of musical-object)
note-transform)
(transform (second-structure-of musical-object)
note-transform)))))
[to do: in (draw (transform ....)) voorbeelden, orginal-and-transform doen? ]
We can now express both mirror- note- around- middle- c and transpose- note- semitone with one transform function:
(transform '(sequential (note 1 60 1)(note 2 63 1))
#'transpose-note-semitone) ->
(sequential (note 1 61 1)(note 2 64 1))
(transform '(sequential (note 1 60 1)(note 2 63 1))
#'mirror-note-around-middle-c) ->
(sequential (note 1 60 1)(note 2 57 1))
Note the use of the #' construct (called the function quote) which is used to signal to Lisp that the following expression is to be considered as a function. Next, we will define some more useful note-transformations:
(defun twice-note (note)
"Return a sequence of two notes"
(make-sequential note note))
(defun half-note (note)
"Return a note with half the duration"
(make-note :duration (/ (duration note) 2.0)
:pitch (pitch note)
:loudness (loudness note)))
(defun double-note (note)
"Return a doubled note"
(twice-note (half-note note)))
(double-note '(note 0.5 60 1)) ->
(sequential (note 0.25 60 1) (note 0.25 60 1))
The function double- note transformes a note into a sequence of two notes with half the original duration. It is built from two other transformations. The first one, half- note, divides the duration of its argument by two. The second, twice- note, makes a sequence of two identical copies of its argument. We can now use this function in combination with our transform function, doubling every note in the musical object.
(transform (example) #'double-note) ->
(sequential (parallel (sequential (note 0.5 60 1)(note 0.5 60 1))
(sequential (note 1 63 1)(note 1 63 1)))
(sequential (note 2 55 0.5)(note 2 55 0.5)))
(draw (transform (example) #'double-note)) =>
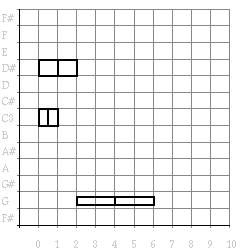
Figure 4. Example transformed with double-note
The use of functions as arguments (so called downward funargs) seems to give so much extra power that we might begin to wonder what good the passing of functions as results (so called upward funargs) could give us.
If we wanted to apply an octave transposition to a structure we would have to write a new function, transpose- note- octave, and use it as an argument for transform.
(defun transpose-note-octave (note)
"Return a note transposed by an octave"
(transpose-note note 12))
(transform (example) #'transpose-note-octave) ->
(sequential (parallel (note 1 72 1)
(note 2 75 1))
(note 4 67 0.5))
This means we always have to define the possible transformations in advance. This is not satisfactory and instead we could use anonymous functions as an argument to the transform function. Anonymous functions are not as bad as they look. They are merely a consequence of the rule of first class citizens. For example, it is perfectly normal for objects like numbers, lists and strings to have a notation for the constant values (you can write (+ 1 1) if you need to notate the constant 2). Functions should also have this property. The anonymous function of one argument (note), that will transpose a note by an octave, can be notated like this:
#'(lambda (note) (transpose-note note 12))
(funcall #'(lambda (note) (transpose-note note 12)) '(note 1 60 1)) ->
(note 1 72 1)
This kind of function can be used as argument to the transpose function (remember the function-quote):
(transform (example) #'(lambda (note) (transpose-note note 12))) ->
(sequential (parallel (note 1 72 1) (note 2 75 1)) (note 4 67 0.5))
(transform (example)
#'(lambda (note) (mirror-note note 60))) ->
(sequential (parallel (note 1 60 1) (note 2 57 1)) (note 4 65 0.5))
Still this is a little tedious to do, we have to construct a new anonymous function for every transposition interval or mirroring pitch. We can, however, with the tools we have now, define the functions that will calculate these transposition and mirror functions when given the appropiate argument: functions that construct functions according to our definitions ( program generators). This is a very powerful mechanism.
(defun transpose-note-transform (interval)
"Return a function for transposing a note by interval"
#'(lambda (note) (transpose-note note interval)))
(defun mirror-note-transform (center)
"Return a function for mirroring a note around a center"
#'(lambda (note) (mirror-note note center)))
(draw (transform (example) (transpose-note-transform 2))) =>
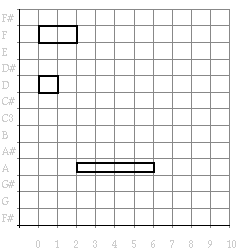
Figure 5. Example transformed with transpose-note-transform
(draw (transform (example) (mirror-note-transform 59))) =>
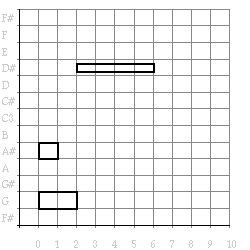
Figure 6. Example transformed with mirror-note-transform
When we add an extra &rest argument args, our transform can also be used with note transformations of more than one argument:
(defun transform (musical-object note-transform &rest args)
"Return a transformed musical object"
(case (structural-type-of musical-object)
(note
(apply note-transform musical-object args))
(sequential
(make-sequential (apply #'transform
(first-structure-of musical-object)
note-transform
args)
(apply #'transform
(second-structure-of musical-object)
note-transform
args)))
(parallel
(make-parallel (apply #'transform
(first-structure-of musical-object)
note-transform
args)
(apply #'transform
(second-structure-of musical-object)
note-transform
args)))))
(draw (transform (example) #'limit-loudness 0.5 0.8)) =>
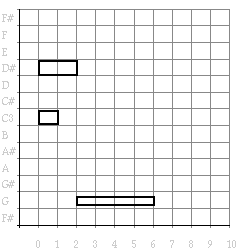
Figure 7. Loudness transformed example
(draw (transform (example) #'transpose-note 3)) =>
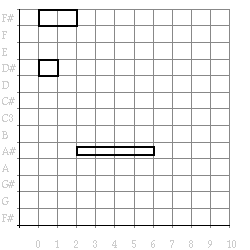
Figure 8. Pitch transformed example
Note that we had to change the funcall of the note-transform into an apply and add an apply before every call to transform. Apply is needed when there a list of arguments, each of which should be individually communicated to the applied function. The last argument to apply should be a list. Compare their use in the following examples:
(funcall #'make-sequential '(note 1 60 1) '(note 1 62 1)) ->
(sequential (note 1 60 1) (note 1 62 1) )
(apply #'make-sequential '((note 1 60 1)(note 1 62 1))) ->
(sequential (note 1 60 1) (note 1 62 1))
(apply #'make-sequential '(note 1 60 1) '((note 1 62 1))) ->
(sequential (note 1 60 1) (note 1 62 1))
[to do: iets over eval, apply, &rest interactie hier ]
Functional programming makes it possible to construct very general programs that are customized for specific purposes. These are the tools that are badly needed in software design. They deserve to be supplied in software libraries, so that programmers can stop reinventing the wheel each time. As a tool for composers these programs may aim to be as 'empty' as possible, only expressing general abstract knowledge about musical structure and leaving open details about the specific material and relations used. The transformations we have so far designed are not yet that general. They were structure preserving, and thus a transformation of a sequence would always yield a sequence. Only at the note level could the structure expand into a bigger one (e.g., when using double- note). Bearing this in mind we are going to develop a more general transformation device.
Our new transformation is like the old one, except that it takes two more arguments to calculate what a sequential, and what a parallel structure transforms into:
(defun transform (musical-object sequential-transform
parallel-transform
note-transform
&rest args)
"Return a transformed musical object"
(case (structural-type-of musical-object)
(note
(apply note-transform musical-object args))
(sequential
(funcall sequential-transform
(apply #'transform
(first-structure-of musical-object)
sequential-transform
parallel-transform
note-transform
args)
(apply #'transform
(second-structure-of musical-object)
sequential-transform
parallel-transform
note-transform
args)))
(parallel
(funcall parallel-transform
(apply #'transform
(first-structure-of musical-object)
sequential-transform
parallel-transform
note-transform
args)
(apply #'transform
(second-structure-of musical-object)
sequential-transform
parallel-transform
note-transform
args)))))
We now have available a very powerful transformation device. First a rather stupid example of its use: the identity (i.e. no tranformation) transformation which just rebuilds its arguments.
(defun no-note-transform (note)
"Return untransformed note"
note)
(transform (example) #'make-sequential #'make-parallel #'no-note-transform) ->
(sequential (parallel (note 1 60 1)
(note 2 63 1))
(note 4 55 0.5))
In Figure 9 is shown how the results (i.e. musical structures) are passed upward by no- note- transform, make- parallel and make- sequential .
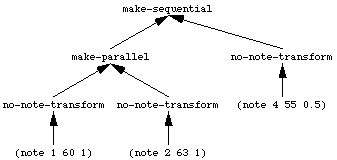
Figure 9. Evaluation hierarchy.
[to do: these trees should be eval-hierarchies ]
Now some more useful transformations can be constructed. The results that are passed upward are numbers. The first transformation calculates the duration of a complex musical structure by adding or maximizing the duration of substructures: adding durations for sequential structures, and taking the maximum of each element for parallel structures:
(defun duration-of (musical-object)
"Return duration of musical object"
(transform musical-object #'+ #'max #'duration))
Similarly it is possible to calculate the duration of the longest note, the number of notes in a piece and the maximum number of parallel voices of a complex structure. Note how easy the transform function is adapted to these different purposes by 'plugging in' different functional arguments.
(defun longest-note-duration (musical-object)
"Return longest-note-duration in musical object"
(transform musical-object #'max #'max #'duration))
(defun count-one (note)
"Return the number 1"
1)
(defun number-of-notes (musical-object)
"Return the number of notes in musical object"
(transform musical-object #'+ #'+ #'count-one))
(defun max-number-of-parallel-voices (musical-object)
"Return the maximum number of parallel voices in musical object"
(transform musical-object #'max #'+ #'count-one))
(duration-of (example)) -> 6
(longest-note-duration (example)) -> 4
(number-of-notes (example)) -> 3
(max-number-of-parallel-voices (example)) -> 2
Figures 10to 13show the way information is communicated upward in the different uses of transform.
[to do: these trees should be eval-hierarchies ]
Figure 10. (duration-of (example)) -> 6
![]()
Figure 11. (longest-note-duration (example)) -> 4
![]()
Figure 12. (number-of-notes (example)) -> 3
![]()
Figure 13. (max-number-of-parallel-voices (example)) -> 2
To demonstrate again the generality of the transform, we will now write a program to draw a piano-roll notation of a musical structure as shown in previous figures. To draw a note at the correct place we need to know the absolute start time of a musical object, information that neither the notes or the transform function itself supplies. When context information is missing, it is a well known trick in AI programming, to calculate a function of the (not yet known) context as temporary result. We could use such a solution here. draw- note function returns a function that will draw a graphical representation of a note when given a start time. As the drawing is done as a side- effect, this function can then return the end time of the note as context (start-point) to use in further drawing. draw- sequential function receives two such draw-functions as arguments and constructs the draw function that will pass its start time to the first and pass the end time returned by the first to the second, returning its end time as the result. function draw- parallel will pass its start time to both sub-structure draw functions returning the maximum end time they return. Thus not numbers or musical structures are passed upward as result of the transformation on sub-structures, but functions that can draw the sub-structure when given a start time. function draw- musical- object just has to apply the draw function resulting from the call to transform to time 0. function draw is the top level function that constructs a graphical window using make- draw- window (that we will be described in section 3.1: object oriented I) and applied our draw- musical- object to it.
(defun draw (musical-object &rest args)
"Make a window and draw the musical object on it"
(let ((window (apply #'make-piano-roll-window args)))
(draw-musical-object musical-object window)
window))
(defun draw-musical-object (musical-object window)
"Draw a musical object on window"
(funcall (transform musical-object
#'draw-sequential
#'draw-parallel
#'draw-note
window)
0))
(defun draw-note (note window)
"Return end time of note, drawn as side effect"
#'(lambda (time)
(draw-horizontal-block time ; x-position
(pitch note) ; y-position
(duration note) ; width
(loudness note) ; height
window) ; output window
(+ time (duration note)) ; end time
))
(defun draw-sequential (a b)
"Return end time of sequential object"
#'(lambda (time)
(funcall b (funcall a time))))
(defun draw-parallel (a b)
"Return end time of parallel object"
#'(lambda (time)
(max (funcall b time)
(funcall a time))))
(defun draw-horizontal-block (left middle width height window)
"Draw block on window"
(let* ((right (+ left width))
(top (+ middle (* height .5)))
(bottom (- middle (* height .5)))
(boundary (list left top right bottom)))
(draw-rectangle window boundary) ; assumed graphical primitive
window))
(draw (example)) =>

Figure 14. The piano roll representation of the example.
Since it turned out to be so useful to be able to talk about functions as objects which are passed to and from other functions, we are now going to examine the possibilities of a special kind of these "other" functions, called combinators. A combinator is a higher order function that has only functions as arguments and return s a function as a result. The first one we will show is the combinator called twice:
(defun twice (transform)
"Return a function that applies a transform twice"
#'(lambda(object)
(funcall transform (funcall transform object))))
(funcall (twice #'rest) '(1 2 3 4 5)) -> (3 4 5)
It can double the action of any function. and therefore (twice #'rest) will be a function that removes the first two elements from a list. (twice #'transpose- note- octave) will yield a function that transposes notes two octaves and (twice #'mirror- note- around- middle- c) will be a useless transformation (the identical transformation).
(transform (example)
#'make-sequential
#'make-parallel
(twice #'transpose-note-octave)) ->
(sequential (parallel (note 1 84 1)
(note 2 87 1))
(note 4 79 .5))
The second combinator is the "function-composition" combinator. It can combine the actions of two transformations into a new one.[18].
(defun compose (transform-1 transform-2)
"Return function composes of two other functions"
#'(lambda(object)
(funcall transform-1 (funcall transform-2 object))))
(funcall (compose #'first #'rest) '(c d e f g a b)) -> d
To construct a transformation that is a doubling applied to the result of an octave transposition we could use this combinator to build it.
(transform (example)
#'make-sequential
#'make-parallel
(compose #'double-note #'transpose-note-octave)) ->
(sequential
(parallel (sequential (note .5 72 1)(note .5 72 1))
(sequential (note 1 75 1)(note 1 75 1)))
(sequential (note 2 67 .5)(note 2 67 .5)))
(draw (transform (example)
#'make-sequential
#'make-parallel
(compose #'double-note #'transpose-note-octave))) =>
Figure 15. The piano roll representation of doubled and transposed notes.
Note that in Figure 15 the y-axis is adapted.
To show the usefulness of these constructions, we will write a function that calculates a complex melody from a simple one by adding a parallel melody that is the doubling of the original one transposed one octave. This is a transformation often used in Javanese Gamelan music. The score of the add- doubled transformation on the example object is shown in Figure 16.
(defun add-doubled (musical-object)
"Return a musical-object with itself doubled and octave higher added"
(make-parallel musical-object
(transform musical-object
#'make-sequential
#'make-parallel
(compose #'double-note
#'transpose-note-octave))))
(draw (transform (example) #'make-sequential #'make-parallel #'add-doubled)) =>

Figure 16. The piano roll representation of add-doubled transformation.
Note that we could have defined twice as a composition of a transform with itself:
(defun twice (transform)
"Return a function that applies a transform twice"
(compose transform transform))
Next we will write some logical combinators that take predicte as argument and return a new one. A simple compose- and- 2, composing two predicates would look like this:
(defun compose-and-2 (predicate-a predicate-b)
"Return predicate that is a logical and of predicates"
#'(lambda(&rest args)
(and (apply predicate-a args)
(apply predicate-b args))))
(funcall (compose-and-2 #'note?
#'middle-c?)
'(note 1 60 1)) ->
(note 1 60 1)
We use a &rest lambda-list keyword and an apply to make it work for predictates that take more than one argument.
Next we can write a compose- and and compose- or that can take more than two predicates as follows:
(defun compose-and (predicate &rest predicates)
"Return predicate that is a logical and of predicates"
#'(lambda(&rest args)
(and (apply predicate args)
(apply (apply #'compose-and predicates) args))))
(defun compose-or (predicate &rest predicates)
"Return predicate that is a logical or of predicates"
#'(lambda(&rest args)
(or (apply predicate args)
(apply (apply #'compose-or predicates) args))))
Below a predicate that tests whether the argument is a sounding middle-c:
(funcall (compose-and #'note?
#'sounding-note?
#'middle-c?)
'(note 1 60 0)) ->
nil
We will now return to our transform function. We saw that it was a general solution for dealing with context information. However, this will not be always the best solution. When information like start-time is used a lot, it may be wiser to adapt the transform function itself so that it passes this information as well to the note-transformation function. Instead of rewriting transform itself, we will wrap a function of time around our sequential, parallel en note-transform arguments, such that they can be used in our existing transform function.
(defun timed-transform (musical-object time
sequential-transform
parallel-transform
note-transform
&rest args)
"Return a transformed musical object"
(first (funcall (apply #'transform
musical-object
(wrap-sequential sequential-transform)
(wrap-parallel parallel-transform)
(wrap-note note-transform)
args)
time)))
We will start by writing the note wrapper. wrap- note will return a function of one argument (the note object), but will apply the transform to both the note and time:
(defun wrap-note (transform)
"Return a note transform that has access to its start-time"
#'(lambda(note &rest args)
#'(lambda(time)
(apply transform note time args))))
Next we rewrite it to return both the transformed note and the end time. In the draw code, where we used this technique for the first time, we could just return the end times of notes (to be used, e.g., to calculate the start time of the next note) because drawing was done as a side-effect. Here we do need the transformed objects as well, so we return both values, the transformed note and its end time, in a list:
(defun wrap-note (transform)
"Return a note transform that has access to its start-time"
#'(lambda(note &rest args)
#'(lambda(time)
(list (apply transform note time args)
(+ time (duration note))))))
The seguential and parallel wrappers will collect these values, apply their transform, and communicate the new objects and end times:
(defun wrap-sequential (transform)
"Return a sequential transform that has access to its start-time"
#'(lambda(object-a object-b)
#'(lambda(time)
(destructuring-bind (result-a end-a) (funcall object-a time)
(destructuring-bind (result-b end-b) (funcall object-b end-a)
(list (funcall transform result-a result-b)
end-b))))))
(defun wrap-parallel (transform)
"Return a sequential transform that has access to its start-time"
#'(lambda(object-a object-b)
#'(lambda(time)
(destructuring-bind (result-a end-a) (funcall object-a time)
(destructuring-bind (result-b end-b) (funcall object-b time)
(list (funcall transform result-a result-b)
(max end-a end-b)))))))
The function wrap- sequential applies a wrapped object- a (a note, sequential or parallel object) to the current time, collects its result and end time, and then applies the other wrapped obect (object- b) to this end time. Next the transform function is applied to both results and returned with the end time of the last object in the sequence. The function wrap- parallel does a similar thing, however apllied both wrapped objects to the same time and returns the maximim of both end times. This is advanced use of functions, so take your time in understanding it.
With our new timed- tranform our previous piano-roll drawing code becomes obsolete: we just need to communicate a draw-function for notes, and do nothing otherwise:
(defun nothing (&rest ignore)
"Return nil and do nothing"
nil)
(defun draw-musical-object (musical-object window)
"Draw a musical object on window"
(timed-transform musical-object
0
#'nothing
#'nothing
#'(lambda(note time window)
(draw-horizontal-block time
(pitch note)
(duration note)
(loudness note)
window))
window))
(draw (example)) =>
Figure 17. Piano-roll example using timed-transform.
We now can built transformations, such as a fade- out (decrescendo), that are time dependent. For that, we first will make a time function. The function decline- time- function is a constructor function: it returns a function of time. It will return values from 1 to 0 (linearly interpolated) over the interval defined by begin and end.
(defun decline-time-function (begin end)
"Return a time-function, a ramp from 1 to 0 over interval [begin, end]"
#'(lambda (time)
(- 1.0
(/ (- time begin)
(- end begin)))))
(funcall (decline-time-function 0 10) 0) -> 1.0
(funcall (decline-time-function 0 10) 2) -> 0.8
We use this function to write a fade- out- transform for notes, scaling the loudness of notes with this time-function.
(defun fade-out-transform (begin end)
"Return note with decresenco applied to it"
#'(lambda (note time)
(if (< begin time end)
(make-note :duration (duration note)
:pitch (pitch note)
:loudness (* (loudness note)
(funcall (decline-time-function begin end) time)))
note)))
fade- out- transform returns a function of two arguments. This function, when applied to a note at a certain time, will return a new note with a loudness depending on the position within the time interval delimited by begin and end.
(draw (timed-transform (make-sequential (example) (example))
0
#'make-sequential
#'make-parallel
(fade-out-transform 0 11))) =>
Figure 18. fade-out example
Sometimes we wish to transform our musical objects to note lists where we add the start time of each note. For example, when we want to play our musical object. All that is required is a function to transform a note to a data structure containing the note and its start time: a timed note. We add a new contructor and two accessors:
(defun make-timed-note (note onset)
"Return a note with start time"
(list (list onset note)))
(defun start-of (timed-note)
"Return start-time of timed-note data structure"
(first timed-note))
(defun note-of (timed-note)
"Return note of timed-note data structure"
(second timed-note))
We can now write a function musical- object- to- note- list that transforms one of our musical objects into a flat list of notes, using our new timed- tranform. In the case of notes we add the start-time to it (with make- timed- note) and add . For sequential objects we simply append its elements, since they are already in the right time order. Only for parallel objects we have to do a little more work. Its elements, which will be two note lists in the right order, will have to be merged. For this we write the function merge- note- lists which takes two note-lists and, depending on the onset of the notes, conses the first note of one list or the first note of the other in the resulting merged list, and this of course recursively. Note the more elaborate list-recursion template used here, with two stop-conditions, an extra test, and two recursive constructions.
(defun merge-note-lists (list-1 list-2)
"Return merged notes list"
(cond ((null list-1) list-2)
((null list-2) list-1)
((<= (start-of (first list-1))
(start-of (first list-2)))
(cons (first list-1)
(merge-note-lists (rest list-1) list-2)))
(t (cons (first list-2)
(merge-note-lists list-1 (rest list-2))))))
(defun musical-object-to-note-list (musical-object)
"Return a flat note-list derived from musical object"
(timed-transform musical-object
0
#'append
#'merge-note-lists
#'make-timed-note))
(musical-object-to-note-list (example)) ->
((0 (note 1 60 1)) (0 (note 2 63 1)) (2 (note 4 55 0.5)))
Using this function we can play the example (readers we will just to have to look at it).
(defun play (musical-object)
"Play a musical object"
(play-notes (musical-object-to-note-list musical-object)))
Figure 19. Score of the played example.
Finally, we will improve of our constructors make- sequential and make- parallel such that they are not restricted to two arguments. We can use the lambda-list keyword &rest that signals Lisp to collect all the arguments of the function in a list:
(defun make-sequential (&rest elements)
"Return a sequential data structure"
(cons 'sequential elements))
(defun make-parallel (&rest elements)
"Return a parallel data structure"
(cons 'parallel elements))
(defun elements (structured-object)
"Return elements of object"
(rest structured-object))
(make-sequential (make-note :duration 1 :pitch 60)
(make-note :duration 1 :pitch 62)
(make-note :duration 1 :pitch 63)) ->
(sequential (note 1 60 1)(note 1 62 1)(note 1 63 1))
(elements '(sequential (note 1 60 1)(note 1 62 1)(note 1 63 1))) ->
((note 1 60 1)(note 1 62 1)(note 1 63 1))
We have to adapt transform to deal with these new definitions, using mapcar to iterate the transform over all the elements of a sequential or parallel structure:
(defun transform (musical-object sequential-transform
parallel-transform
note-transform
&rest args)
"Return a transformed musical object"
(case (structural-type-of musical-object)
(note (apply note-transform musical-object args))
(sequential
(apply sequential-transform
(mapcar #'(lambda(element)
(apply #'transform
element
sequential-transform
parallel-transform
note-transform
args))
(elements musical-object))))
(parallel
(apply parallel-transform
(mapcar #'(lambda(element)
(apply #'transform
element
sequential-transform
parallel-transform
note-transform
args))
(elements musical-object))))))
(defun timed-transform (musical-object time
sequential-transform
parallel-transform
note-transform
&rest args)
"Return a transformed musical object"
(first (funcall (apply #'transform
musical-object
(wrap-sequential sequential-transform)
(wrap-parallel parallel-transform)
(wrap-note note-transform)
args)
time)))
The wrappers for our timed- transform, that uses our newly defined transform (code repeated above), can be simplified a lot using a sequential and parallel iterator that communicate the approiate end-time to the transformation functions:
;;; iterators
(defun sequential-iterator (funs time &optional results)
"Return result of applying transformations sequentically"
(if (null funs)
(list (reverse results) time)
(destructuring-bind (result end) (funcall (first funs) time)
(sequential-iterator (rest funs) end (cons result results)))))
(defun parallel-iterator (funs time &optional results (max time))
"Return result of applying transformations in parall"
(if (null funs)
(list (reverse results) max)
(destructuring-bind (result end) (funcall (first funs) time)
(parallel-iterator (rest funs) time (cons result results) (max end time)))))
;;; wrappers
(defun wrap-sequential (transform)
"Return a sequential transform that has access to its start-time"
#'(lambda(&rest wrapped-objects)
#'(lambda(time)
(destructuring-bind (results end)
(sequential-iterator wrapped-objects time)
(list (apply transform results) end)))))
(defun wrap-parallel (transform)
"Return a parallel transform that has access to its start-time"
#'(lambda(&rest wrapped-objects)
#'(lambda(time)
(destructuring-bind (results end)
(parallel-iterator wrapped-objects time)
(list (apply transform results) end)))))
(defun wrap-note (transform)
"Return a note transform that has access to its start-time"
#'(lambda(note &rest args)
#'(lambda(time)
(list (apply transform note time args)
(+ time (duration note))))))
(defun large-example ()
"Return large musical object"
(make-sequential (example) (example) (example)))
(draw (timed-transform (large-example)
0
#'make-sequential
#'make-parallel
(fade-out-transform 0 18))) =>
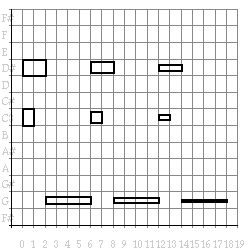
Figure 20. Piano-roll of larger example.
defun can be considered as a device that makes the definition of a function easier to read, but it assumes the name of the function and the function body itself to be constants. define- function is a similar construct that gives a little bit more power than defun that we can use for calculation functions. We will make this construct in chapter nil: imperative styleor (CHAPTER-REF "embedded style")??, for now we will just use it. It takes a name, an anonymous function, and a documentation string. The following expression (re)defines the function duration
(define-function duration
#'(lambda(note) (second-element note))
"Return the duration of note")
With this construct we can calculate a function body instead of using a constant anonymous function. In the example below we calculate one using one of the transformations defined before.
(define-function transpose-note-octave
(transpose-note-transform 12)
"Return a note transposed by an octave")
(transpose-note-octave '(note 1 60 1)) -> (note 1 72 1)
Note that in the definitions above the formal parameters, which appeared in the argument list of the defun form, are no longer needed. If we have access to enough combinators like twice and compose, we can even completely do without parameters.
(define-function double-note
(compose #'twice-note #'half-note)
"Return a doubled note")
(define-function double-and-raise-note
(compose #'double-note #'transpose-note-octave)
"Return a doubled note one octave higher")
(double-and-raise-note '(note 1 60 1)) ->
(sequential (note 0.5 72 1) (note 0.5 72 1))
Languages built on combinators using parameter-freeprogramming are very useful in domains centered around one type of object and many transformations on this object (like the musical structures in our examples). In these domains they facilitate the definition of higher levels of abstraction whereby transformations are considered objects in their own right, so that they can be manipulated, combined and modified. However, when dealing with functions of many arguments we need a lot of combinators for juggling with the order of arguments leading to programs that are difficult to read. For humans, an extra hook into our memory, by means of a mnemonic parameter name, is often indispensable. In addition more heterogeneous domains consisting of different sorts of objects, all subjected to transformations that are conceptually more or less the same, can be modelled better using another style of programming in Lisp. In this style named Object Oriented Programming it is straightforward to express, for example, how both a melody and a synthesizer can have their own definition of transposition. This is the subject of Chapter chapter nil: Object oriented. In the next chapter (chapter nil: imperative style) we will elaborate the use of program generators using define- function.
draw-musical-object (musical-object window) function
a musical object on window
draw-horizontal-block (left middle width height window) function
block on window
draw (musical-object &rest args) function
a window and draw the musical object on it
play (musical-object) function
a musical object
semitone-factor nil function
a constant factor
example nil function
a constant musical object
double-note (note) function
a doubled note
amplitude-to-dynamic-marking (value) function
a dynamic marking associated with an amplitude value
musical-object-to-note-list (musical-object) function
a flat note-list derived from musical object
mirror-note-transform (center) function
a function for mirroring a note around a center
transpose-note-transform (interval) function
a function for transposing a note by interval
twice (transform) function
a function that applies a transform twice
integrate (numbers &optional (offset 0)) function
a list of integrated numbers, starting from offset
transpose-note-list-semitone (notes) function
a list of notes transposed by a semitone
mirror-around-middle-c (musical-object) function
a musical object mirror around middle c
transpose-semitone (musical-object) function
a musical object transposed by a semitone
add-doubled (musical-object) function
a musical-object with itself doubled and octave higher added
make-note (&key (duration 1) (pitch 60) (loudness 1)) function
a note data structure
wrap-note (transform) function
a note transform that has access to its start-time
transpose-note-octave (note) function
a note transposed by an octave
half-note (note) function
a note with half the duration
make-timed-note (note onset) function
a note with start time
make-parallel (&rest elements) function
a parallel data structure
wrap-parallel (transform) function
a parallel transform that has access to its start-time
retrogarde (notes &optional result) function
a reversed note list
accumulating-retrogarde (notes result) function
a reversed note list, an auxiliary function
twice-note (note) function
a sequence of two notes
make-sequential (&rest elements) function
a sequential data structure
wrap-sequential (transform) function
a sequential transform that has access to its start-time
decline-time-function (begin end) function
a time-function, a ramp from 1 to 0 over interval [begin, end]
timed-transform (musical-object time sequential-transform parallel-transform note-transform &rest args) function
a transformed musical object
transform (musical-object sequential-transform parallel-transform note-transform &rest args) function
a transformed musical object
structural-type-of (musical-object) function
a type of a musical object
dynamic-marking-to-amplitude (mark) function
an amplitude value associated with a dynamic marking
duration-of (musical-object) function
duration of musical object
elements (structured-object) function
elements of object
draw-note (note window) function
end time of note, drawn as side effect
draw-parallel (a b) function
end time of parallel object
draw-sequential (a b) function
end time of sequential object
fourth-element (list) function
fourth element of list
compose (transform-1 transform-2) function
function composes of two other functions
large-example nil function
large musical object
longest-note-duration (musical-object) function
longest-note-duration in musical object
merge-note-lists (list-1 list-2) function
merged notes list
minimum (a b) function
minimum value of a and b
nth-element (n list) function
n-th element of list (zero-based)
nothing (&rest ignore) function
nil and do nothing
mirror-note (note center) function
note mirrored around center
mirror-note-around-middle-c (note) function
note mirrored around middle-c
note-of (timed-note) function
note of timed-note data structure
transpose-note (note interval) function
note transposed by interval
transpose-note-semitone (note) function
note transposed by semi-tone
limit-loudness (note low high) function
note with clipped loudness
fade-out-transform (begin end) function
note with decresenco applied to it
exponent (number power) function
number raised to power
transpose-pitch (pitch interval) function
pitch increased by interval
mirror-pitch (pitch center) function
pitch mirrored around center
compose-and (predicate &rest predicates) function
predicate that is a logical and of predicates
compose-and-2 (predicate-a predicate-b) function
predicate that is a logical and of predicates
compose-or (predicate &rest predicates) function
predicate that is a logical or of predicates
parallel-iterator (funs time &optional results (max time)) function
result of applying transformations in parall
sequential-iterator (funs time &optional results) function
result of applying transformations sequentically
second-element (list) function
second element of list
start-of (timed-note) function
start-time of timed-note data structure
loudness (note) function
the amplitude of note
duration (note) function
the duration of note
first-structure-of (musical-object) function
the first element of a musical object
max-number-of-parallel-voices (musical-object) function
the maximum number of parallel voices in musical object
count-one (note) function
the number 1
number-of-notes (musical-object) function
the number of notes in musical object
pitch (note) function
the pitch of note
second-structure-of (complex-structure) function
the second element of a musical object
clip (min value max) function
the value, clipped within [min,max]
third-element (list) function
third element of list
sounding-note? (note) function
true if amplitude of note is non-zero, false otherwise
note? (object) function
true if note, false otherwise
middle-c? (note) function
true if pitch of note is 60, false otherwise
same-note? (note-1 note-2) function
true when notes are equal, false otherwise
between? (value min max) function
true when value in interval <min, max], false otherwise
no-note-transform (note) function
untransformed note
pitch-to-frequency (pitch) function
a MIDI number into a frequency (in Hz.)
(Barendregt, 198?)
(IMA, 1983)
Object Oriented Programming
abstraction
accumulating parameter
anonymous functions
application
body
combinators
consing
data abstraction
downward funargs
first class citizens
function quote
iteration
lambda-list keywords
lexical scope
list
list iterator
list recursion
numeric recursion
parameter-freeprogramming
part-of hierarchy
predicate
program generators
recursion
side- effect
special form
stack
tail recursion
time function
upward funargs
these trees should be eval-hierarchies
these trees should be eval-hierarchies
iets over interactie hier
in (draw (transform ....)) voorbeelden, orginal-and-transform doen?
ongeveer hier iets over een car/cdr recursie? En, symmetrisch, fun op elements and sub-elements, transpose uitschrijven?
vertaal: detwaalfde machtswortel uit twee
[an error occurred while processing this directive]