Some factories (e.g. voice, measure, group) accept a rhythmical tree as a slot input. Such a tree is a list in the form :
(D S) where
So (1 (1 1 1 1)) is a structure whose extent is, say, a whole-note (1), and which contains 4 equally lasting values, 4 quarter notes inthat case.
(2 ( (1 (1 1 1 1)) (1 (1 1 1 1)) )
is a structure lasting, say, two whole-notes, containing two equal substructures, each lasting a whole-note. These substructures in turn contain 4 equal values i.e. quarter notes. So it can be interpreted as a voice containing 2 measures in 4/4.
When the number D is at the level of a voice, it is by convention expressed in whole-note units.
When the number D is at the level of a measure, it is by convention expressed in whole-note units, and it may also be expressed by a ratio e.g.:
4/4, 7/8, 5/2
or a list e.g. :
(4 4) (7 8) (5 2)
which meaning is the usual musical one for time signature. Due to a specificity of the underlying Common Lisp system, ratios like 4/4 are automatically simplified (i.e. 4/4 = 1). In that case, the list form should be chosen (i.e. (4 4)) or , alternatively, he special notation 4//4.
To avoid tedious calculations, D can be replaced by a question-mark '?'. In that case OM will figure out the actual value of D. Our previous example can then be rewritten as :
(? ( (1 (1 1 1 1)) (1 (1 1 1 1)) )
Here are some examples :
(1 (1 1 1 1 1)) considered as a single group. The choice of the quarter note here is arbitrary.
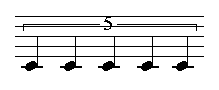
(? ((4//4 (1 (1 (1 -2 1 1)) 1 1)) (4//4 (1 (1 (1 1 1)) -1 1))))
considered as a voice. Note the question mark telling OM that we don't bother with the actual voice duration, and the negative numbers that stand for rests.

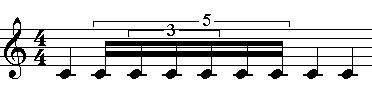
Here we put a triplet inside a quintuplet.
(4//4 (1 (1 (1 (2 (1 1 1)) 1 1)) 1 1)