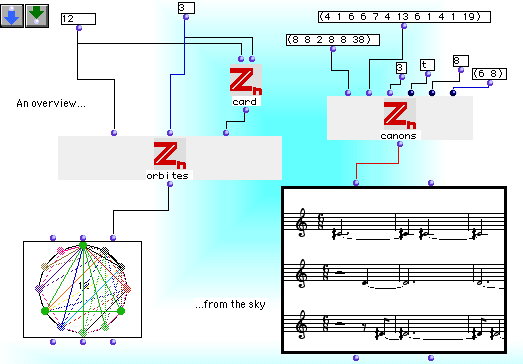
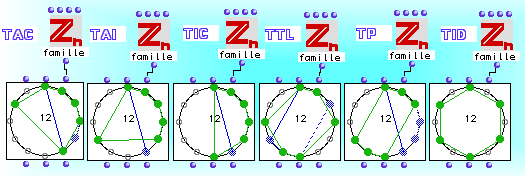
This is a part of the algebraic sky we will try to explore in this library. In the left side you see the cyclic group Zn acting in the pitch domain. The basic philosophy of an algebraic-oriented approach to the formalisation of chords structures is well summarised by the following statement: for any equally tempered division of the musical octave in a number n of parts there is a cyclic group that describes it. By means of this group we can ask for the number of k-chords (i.e. chords having k elements) that are 'qualitatively' different, according to the musical transformation which is canonically associated with: the transposition. We obtain in such a way transposition classes of chords that are called 'orbits', usually represented as polygons in a circle. For example, in the common division of the octave in 12 parts there are 19 different 3-chords (up to transposition), as you can see by evaluating the Zn-card function. All of them are represented in the circle. You can open this box by double clicking in it and see with the help of the letter 'h' the basic options.

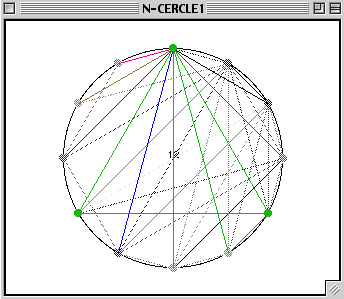
For example, consider the following 3-chords that you have isolated from the remainders by means of 'b' and of the 'change front list' option.

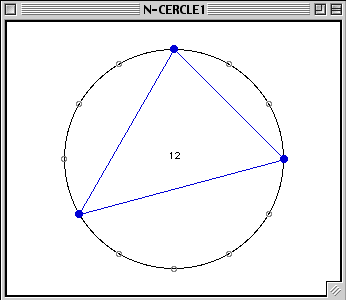
With 'c' you obtain the chord that is complementary to this particular 3-chord, i.e. it consists of all pitches that are not present in this latter. Doing again the complementary means coming back to the 3-chord that we started with. Now try to inverse it with the letter 'i'. This is the resulting chord:

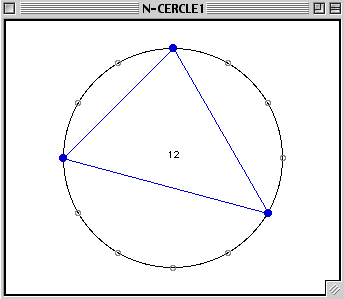
As you see, one pitch has not changed. In fact, inversion means mirror-reflection through an axis (the diameter) and there is no loss of generality in supposing that this axis will be that one connecting the points 0 and 6 in the usual 'clock'-oriented circular representations of pitches (0=do, 1=do#=reb, …, 11=si). In fact, any inversion is a product of this do-based inversion and a transposition (i.e. a rotation). The 'r' option enables transposing a chord by clicking in the point of the circle corresponding to the required transposition. No transpositions of the inverted chord will transform it into the 3-chord that we started with. In other words, this 3-chord is not self-inverse. No question that the complementary could be the same, for only 6-chords may have this self-complementarity. The same conclusion holds if we compare the inversion and the complementary. They are not the same, which means that this 3-chord is not inverse-complementary. It neither belongs to the family TTL of chords having Messiaen' s limited transposition property. In fact, only the augmented 3-chord has this property, as you can verify by looking for 3-chords in the family TTL. Note that you will have no answer if you are asking for more than one solution.

The augmented 3-chord has two more important properties. It is partitioning and idempotent. It is partitioning because the disjoint union of this one and two transpositions of it (respectively of a semitone and a tone) recovers the entire circle. It is idempotent because it corresponds to the subgroup of the cyclic group Z/12Z generated by the major thirds (adding three major thirds to an element means taking the octave of it, i.e. the element itself, because of the equivalence modulo the octave). All these families will be discussed in the second part of the tutorial. Just have a look…

As mentioned in the foreword, some properties of the cyclic group Zn turned out to be particularly relevant in order to study the problem of construction of rhythmic canons tiling musical time space. At the moment the library focuses on the implementation of a family of canons called after Dan Tudor Vuza's model of rhythm "Regular Complementary Canons of Maximal Category" (shortly RCMC-Canons). Here you find an example of such a canon:

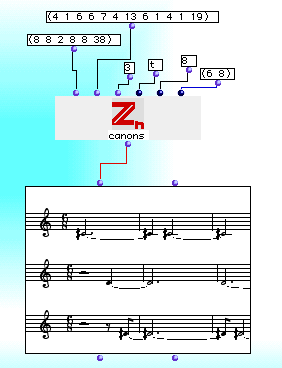
This canon is generated by the rhythmic periodic pattern R=(8 8 2 8 8 38), where the numbers represent the intervals between the onsets. The second rhythmic structure S=(4 1 6 6 7 4 13 6 1 4 1 19), also called 'outer rhythm' specifies (in terms of temporal intervals) when the other voices are coming into. Note that R and S have the same period (this is the maximal category condition). Thanks to the complementarity between the voices (this means neither overlapping nor holes), when all of these are playing, a regular pulsation is perceived. In other words, canons of this type 'tile' the musical time space. We are working in collaboration of the KIT-MaMuTh group of Berlin supervised by Thomas Noll and Guerino Mazzola in order to include the case of canons having voices that are stretched by a given factor. Canons of this type are called by Noll 'augmented canons'.

For the moment we concentrate only on RCMC-Canons. The first part of the tutorial we will progressively present the basic functions that enable obtaining canons of this type.