By definition a chord M in Zn is said to have Messiaen's limited transposition property if it does exist an integer t in Zn (t being different from 0 modulo n) such that t+M=M, where the sum means addition modulo n. The lowest integer t verifying the previous condition is called the 'period' of the chord M. Therefore limited transposition chords are also called periodic chords. In this example we are looking for 6-chords having this property.

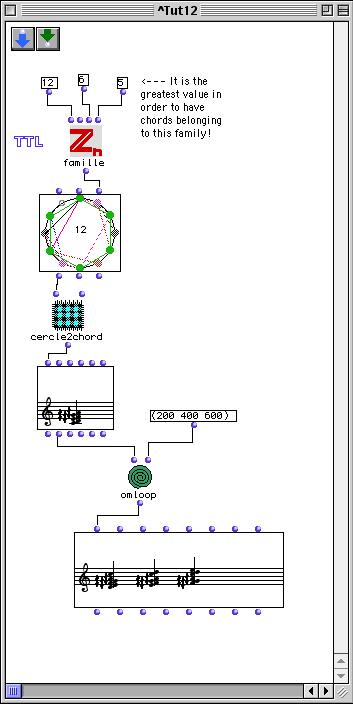
We cannot ask for more than 5 hexachords belonging to the TTL family, otherwise no solution will be given. Double-click in the n-cercle box and see all possibilities with the option 'change front list' (use the letter 'h' for a help). The example shows the chord M=(2 2 2 2 2 2) with three transpositions corresponding to the Z12 integers t=2, t=4, t=6. For all such integers t+M=M. Note that this chord is also belonging to the families TAC, TAI and TIC. Go to the next two tutorials to see why this chord is partitioning and idempotent too.