A chord in Zn is said to be partitioning if the cyclic group is a disjoint union of transposition of the same chords. This means that any pitch-integer of the cyclic group Zn belongs to a transposition (and only one) of the chord.

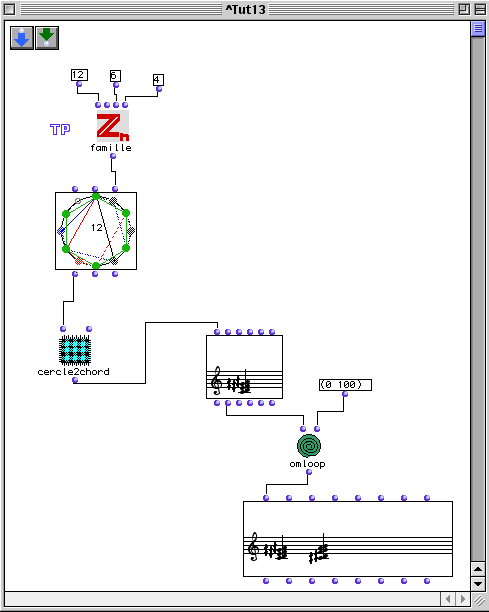
In this example we are asking for partitioning hexachords (only 4 solutions are required).

The first solution is the chord M=(2 2 2 2 2 2) that we mentioned already in the previous tutorial. The union of this chord and its semitone transposition covers all Zn. Obviously, the union is disjoint for the two chords have no elements in common.

See all solutions by double clicking in the n-cercle box. You will discover that Messiaen's limited transposition property is not a necessary condition in order to have a chord belonging to the TP family. In other words there are partitioning chords that are not limited transposition structures.