Formally speaking a chord M of the cyclic group Zn is a said to be an idempotent chord if M*M=M, where * means taking one chord described by the intervallic structure M (say M0) and considering the union of transpositions of this latter by means of the intervallic content expressed by M (this is in fact the generalisation of Boulez 'multiplication d'accords' for any equal division of the octave in n parts, as firstly studied by the Rumanian theoretician and composer Anatol Vieru).

The following example shows that there are no idempotent pentachords in the usual division of the octave

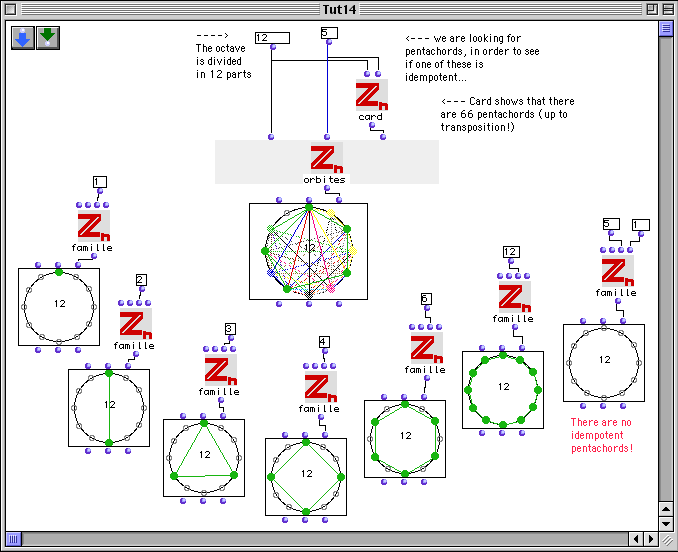
The conclusion is a trivial consequence of the following algebraic statement: the class of idempotent chords is isomorphic to the family of subgroups of the cyclic group Zn. The cardinality of a subgroup must divide the order n of the cyclic groups. This means that idempotent pentachords only exist in a division of the octave in m parts, where m is a multiple of 5.