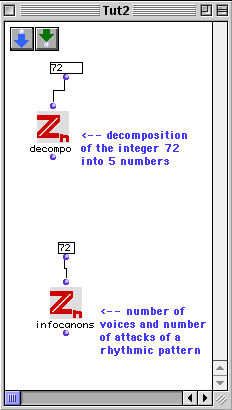
If the period n is a 'good period', we may ask to its decomposition into five numbers (p1 p2 n1 n2 n3) such that:

1) p1 and p2 are different primes

2) The product p1n1 is relatively prime with the product p2n2

3) n3 is an integer greater than 1

Evaluate the output in order to see how the smallest 'good period' can be decomposed.

In the 'infocanons' box we start, as before, with a 'good period', e.g. 72. The evaluation gives a list consisting of two elements: the first one is the number of voices of the canon (i.e. the cardinality of the 'outer rhythm' S), the second one is the number of attacks of a rhythmic pattern (i.e. the cardinality of the 'ground rhythm' R). Note that the product of the two numbers is always equal to the 'good period' that we started with.