This tutorial aims at introducing the enumeration problem for chord structures. With the help of the 'card' function, we will able to answer to questions as the following: how many 7-chords (up to transposition) are there in the division of the octave in 12 parts?

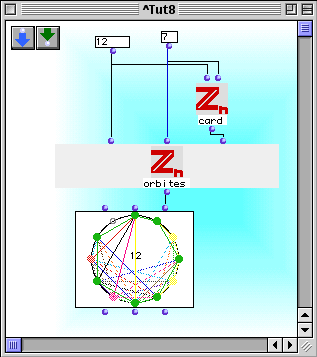
By evaluating the card-box you will see that there are 66 chords of 7 notes (up to transposition). The complete list of these transposition classes, also called orbits, is given by the orbites-box. A chord is usually expressed in terms of pitch-integers. For example the orbit representing the major scale (note that there is no difference between scale and chords in this kind of representation) is expressed by the list (0 2 4 5 7 9 11).

The circular representation is given by means of the class 'n-cercle'.

By double clicking in the n-cercle box you will open an editor that enables some basic manipulation of the chord.

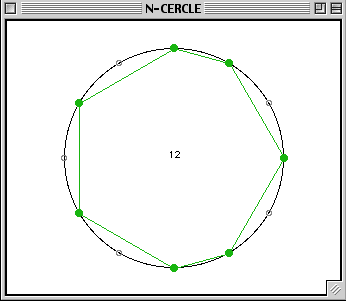
For example, you can eliminate a pitch by clicking on it or add a pitch by clicking in a hole. With the help of the 'h' letter you may have some ideas on the operations that we have already discussed in the overview tutorial. Also notice that you can change the number of division of the octave by clicking in the centre of the circle and moving the mouse up or down.

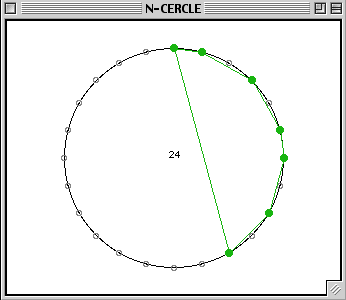
Here you will see the same 7-chord in the division of the octave in 24 parties: