Sans disposer des formalismes combinatoires, Mersenne explore empiriquement des valeurs allant jusqu’à n=22, p = 9, et les 30 partages de p, et trouve, semble-t-il les bonnes réponses.

Le nombre de séquences possibles, exprimé dans le formalisme auquel on est aujourd’hui habitué est:

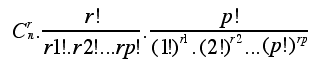
Des problèmes combinatoires aussi complexes ne seront pas réabordés avant Bernoulli, trois-quart de siècle plus tard : les problèmes musicaux sont encore un stimulant des mathématiques " sérieuses ".

Parallèlement aux spéculations sur la consonance des intervalles et la structure diatonique, une approche descriptive du contrepoint se développe au rythme des développements de la polyphonie. Cette démarche est essentiellement non mathématique, ce que l’on comprend bien si l’on considère que les outils formels susceptibles de traiter cette question sont encore inaccessibles. L’approche descriptive constitue progressivement un corpus de règles prescriptives et coercitives sur les enchaînements licites dans la double dimension verticale et horizontale. Le manque de caractère mathématique est aussi lié au statut émergent de la musique comme succession temporelle de choix humains, dans un espace combinatoire contraint par des règles. Il ne s’agit plus en effet de déterminer des propriétés naturelles comme la consonance et de les exprimer dans le formalisme simple de l’arithmétique, comme dans ces systèmes d’engendrement des intervalles par successions des puissances de 2 et de 3, retrouvé dans des manuscrits d’astronomie du XIIème siècle ; il s’agit du déploiement de ces propriétés dans le temps selon une stratégie dont l’objectif est simple (gérer la dialectique du plaisir et du déplaisir).

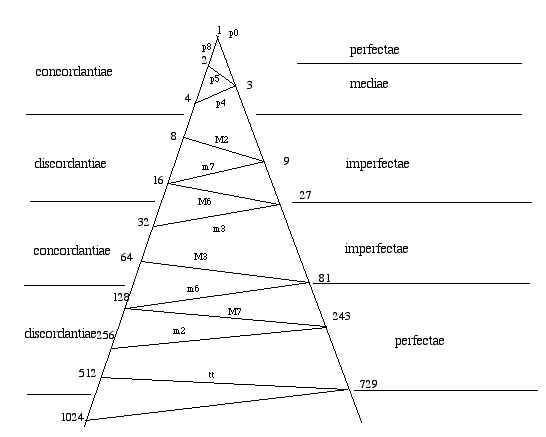
Il est révélateur à cet égard que les calculs combinatoires de Mersennes portent sur des successions monodiques, alors que le corpus théorique traitant du contrepoint est déjà important. Encore ces successions monodiques doivent-elles être considérées comme des structures hors-temps, comme des mots, la formalisation des constructions en-temps restant timide. Notons que si la litanie de ces grands nombres a finalement peu servi les compositeurs, sinon à leur faire sentir le caractère miraculeux du choix qu'opère avec une certaine sûreté le créateur parmi le foisonnement du possible, l'intérêt du texte de Mersenne vient de ce qu'il marque une évolution parallèle de la théorie musicale, qui s'intéresse de plus en plus, au delà du phénomène artificiellement isolé de la consonance, à l'articulation du discours musical dans toutes ses dimensions. On y repère aisément le déplacement d'une conception philosophique de l'univers, d'abord envisagé comme horlogerie immuable, vers la vision inaugurée par Leibniz d'un monde résultant, tel un langage, de l'engendrement combinatoire et exhaustif des possibles.

Cette approche descriptive, au sens de description des règles, qui est le début d’une logique musicale, logique des enchaînements valides, porte en germe l’abolition future de tout déterminisme en musique, dans le sens où, à un ordre naturel, d’essence religieuse ou proto-scientifique, se substitue progressivement un ordre legal, peut être fondée sur l’équivalent d’un droit naturel (ce n’est pas le musicien qui peut décider librement si un intervalle est consonant ou pas), mais qui, par sa nature combinatoire, ouvre un champ de liberté créatrice (ou un champ de rédemption : on peut placer une dissonance, si on s’en repends par une résolution correcte).

Nous avons utilisé le terme logique : en effet, le calcul logique permet d’ériger des systèmes indépendamment des positions d’existence des objets primitifs. Dans le contrepoint, certains énoncés font bien figure d’axiomes (les bons et les mauvais intervalles) et d’autres, de règles d’engendrement des expressions bien formées.

Cette relation avec la logique n’est pas vue à ma connaissance avant le Xxème siècle, c’est à dire avant qu’une compréhension moderne nous informe qu’un système formel peut être bâti sur des axiomes et et des règles de formation arbitraires.

La mutation du compositeur en bâtisseur de système formel est fortement illustrée par la révolution dodécaphonique et sérielle, dans laquelle les axiomes ne sont pas des objets directement dictés par la perception, et les règles de construction s’émancipent totalement du passé. Elle continue sur la lancée avec l’école de Darmstadt et la série généralisée. Elle est enfin menée à un stade proche de la saturation dans la période contemporaine, où l’on voit ce mécanisme de refondation formelle à l’œuvre avec une granularité historique qui n’est plus de l’ordre du siècle ou de la décennie, et qui vient souvent se réduire au temps de gestation d’une composition unique. Ce phénomène est d’ailleurs rendu possible par une utilisation éhontée de l’informatique, ce qui nous rappelle l’enjeu discuté ici, à savoir la calculabilité.

Comme nous y avons déjà insisté, c’est moins avec la logique, au sens habituel du terme, qu’avec celle des systèmes et des langages formels, que le rapprochement de la musique nous semble le plus pertinent. En effet, la logique des prédicats, système formel parmi d’autres, procède-t-elle par un enchaînement de dérivations et de réduction qui finissent par substituer un énoncé, considéré comme final, à un ensemble énoncés constituant des dérivations intermédiaires. Dans le cas musical, l’engendrement temporel ne procède pas véritablement par substitution dans la mesure ou ce qui est dit est dit, et ne vient pas se substituer dans un espace purement formel à une autre expression; au contraire, la perception d’un antécédent conditionne celle d’un conséquent, et la flèche du temps interdit l’écriture d’un signe d’équivalence entre les termes successifs.

Le signe d’équivalence ne pourra être utilisé qu’ entre des termes abstraits de l’élaboration musicale, c’est à dire entre des niveaux successifs de ce que l’on appellera dans la théorie des langages un arbre de syntaxe abstraite, mais en aucun cas entre des termes successifs de la surface musicale, à savoir la frange de l’arbre. De telles substitutions " proche de la surface " ne sont pas absentes de la théorie des langages et apparaissent par exemple dans les grammaires transformationnelles, mais n’opèrent pas entres segments terminaux, les termes concernés disparaissant dans la transformation.

Si l’analogie entre logique musicale et logique tout court ne commence à être discutée que tardivement, c’est qu’elle ne peut émerger qu’après dépassement des théories primitives de la vérité et généralisation de la logique aux systèmes formels, et l’établissement des équivalences théoriques entre ces systèmes et les langages, notamment les équivalences entre décidabilité, calculabilité et reconnaissabilité d’un langage, dont nous parlerons plus loin.

Pour éviter un rapprochement naïf entre logique musicale et logique tout court, il faut se rappeller qu’il n’y a pas de valeur de vérité en musique et qu’il est vain de chercher dans les structures d’enchaînement musical des structures de raisonnement. Par contre il n’est pas du tout absurde de considérer le discours musical, à un certain niveau, comme un langage formel, c’est à dire comme un ensemble d’expressions bien formées relativement à un système de règles et d’objets primitifs posés comme axiomes (ce que certains appellent le matériau) et comme tel de se poser la question de sa calculabilité.

Dans son article Monoïde libre et musique, les musiciens ont ils besoin des mathématiques ? paru en 1987, Marc Chemillier précise : " Parmi les théories présentées ici, certaines s’intéressent à la musique comme organisation d’objets sonores dans le temps, c’est à dire d’une certaine façon à des séquences de symboles : leur cadre abstrait est un monoïde libre A*. Pour d’autres l’étude se porte sur des objets musicaux indépendamment de toute organisation dans le temps (construction des gammes par exemple) ; il s’agit alors d’étudier des structures possibles sur l’alphabet A lui même ".

Le cadre nous semble ici clairement posé. Nous voudrions cependant préciser plus avant le statut du temps dans cette affaire. En effet, la dichotomie instaurée par Chemillier évoque celle, célèbre, proposée par Xenakis sous les termes hors-temps et en-temps, qui nous semble en l’occurence une vision inaboutie de la question. Rappellons brièvement de quoi il s’agit.

La catégorie du hors-temps regroupe des ensembles d’objets, possèdant leurs propre système d’engendrement par loi de composition interne. Ces système d’engendrement sont complètement indépendants de l’ordonnancement qui sera imposé aux objets lorsque ces derniers seront disposés le long l’axe temporel inhérent à la composition. Xenakis y accorde beaucoup d’importance, ces lois sont commutatives, et c’est là probablement leur caractéristique la plus a-temporelle. Lorsque plusieurs paramètres de la musique sont considérés, avec leurs lois de composition, ils forment pour l’auteur un espace vectoriel. Notons que pour Mazzola, la bonne structure pour penser les éléments du vocabulaire musical est le module sur un anneau, soit une structure moins restrictive.

A cela il faut rajouter l’algèbre temporelle, soit une structure d’espace vectoriel de dimension 1 sur les intervalles temporels. Cette dernière structure permet, par concaténation d’intervalles, (cette concaténation n’est pas précisée algébriquement) un repérage de l’axe temporel.

Finalement, une application entre des éléments hors-temps et un repérage particulier de l’axe temporel constitue une structure en-temps.

Georges Bloch a pointé que le hors-temps ainsi défini suppose une conception du matériau comme immanence, que cette immanence soit supposée naturelle ou culturelle, et suppose d’autre part licite les actions de discrétisation nécessaires pour penser ce matériau dans le cadre d’une algèbre commutative.

Nous voulons montrer ici que le fait de rapporter les structures en-temps au mapping final des évènement aux dates est une simplification commode, mais fortement restrictive. Dans le processus qui mène des réservoirs " algébriques " à l’ordonnancement final de la partition, c’est à dire du hors-temps au en-temps, il existe une région intermédiaire dans lesquels la logique d’ordonnancement (les relations de précédence et de simultanéïté entre points remarquables - début, fin, milieu, .. - des évènements sonores ) peut être déjà spécifiée, même si les positions temporelles précises ne sont pas encore définies. Or un grand nombre d’outils formels ont été identifiés qui agissent sur ce niveau logique : théorie des graphes, systèmes de récriture, théorie des grammaires formelles, théorie des automates. Un exemple bien connu en est le système d’engendrement de séquences harmoniques tonales, dont les objets primitifs sont des couples degré, tonalité) et qui peut se penser dans chacun de ces formalismes.

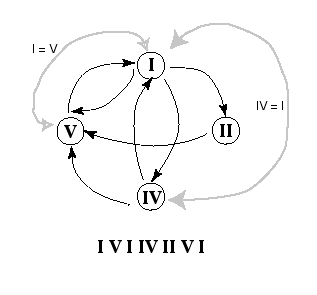
De telles constructions qui évoquent le temps puisqu’elles sont bien des modèles de séquentialité l’évoquent bien plus comme une catégorie logique que comme une catégorie physique. De ce point de vue, ils peuvent aussi avoir une fonction d’immanence par rapport à la composition, et constituer un déjà-là, un inconscient de la partition si l’on veut, qui ne pourra être révélé, à partir de la surface musicale, que par des procédures analytiques.

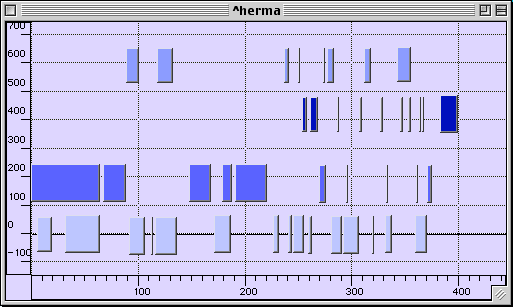
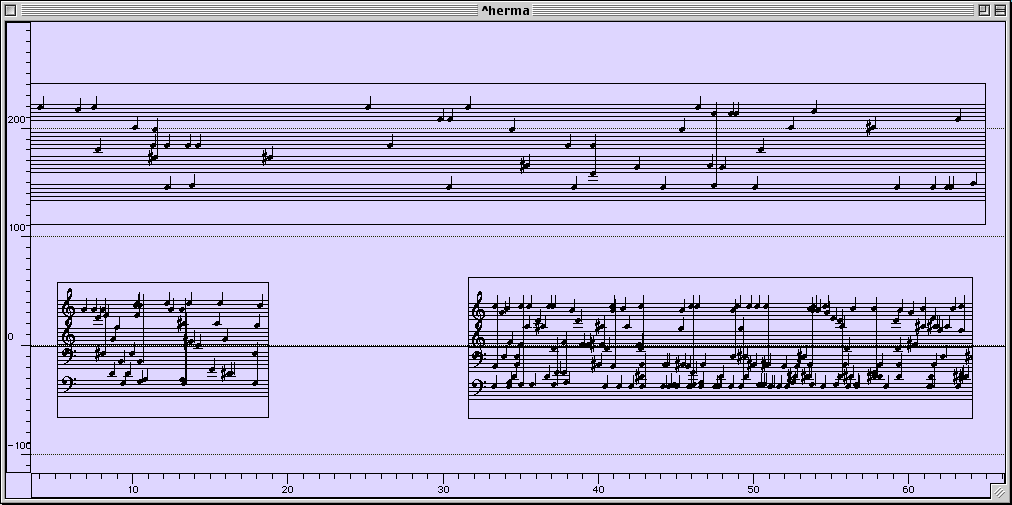
Ces modèles de séquentialité sont souvent, mais pas toujours, des structures de préordre, qui devraient, dans la classification de Xenakis, venir se situer entre l’algèbre hors-temps et l’ordre total du temps physique. Un exemple frappant d’un tel préordre se trouve précisément chez … Xenakis, qui l’utilise mais ne l’identifie pas comme topos, dans la construction de sa pièce Herma pour piano.

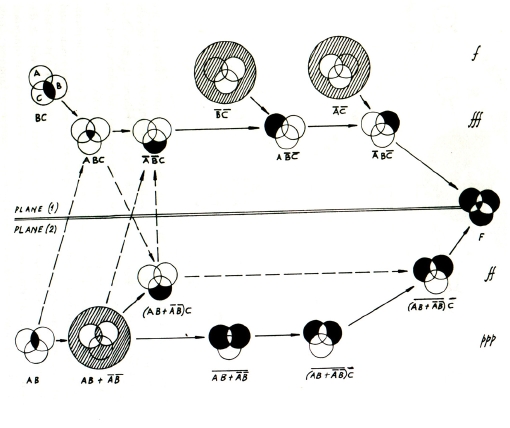
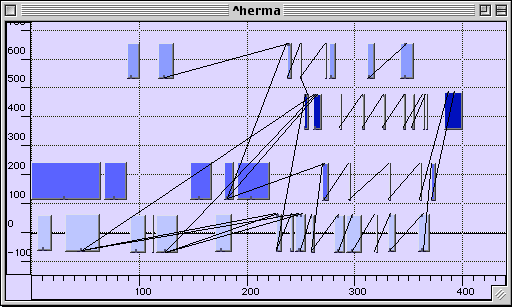
Dans le premier graphe, les flèches entre les ensembles de notes indiquent une préséance liée à l’ordre nécessaire du calcul. Ainsi le dernier ensemble, à droite, représente-t-il le calcul d’une expression booléenne, dont tous les autres sont des étapes. L’ordre de gauche à droite est bien un temps logique, le déroulement du calcul devant se confondre avec celui de la pièce. L’ordre sous-jacent à ce graphe est celui d’un graphe fonctionnel, dans lequel les nœuds sont des opérateurs booleens et les arcs des sous-expressions, qui est donné par ailleurs dans le livre. Le graphe fonctionnel forme bien un treillis, dont la logique d’ordre partiel implique que le réservoir noté doit être exposé après et avant l’expression finale F, mais n’est pas temporellement contraint par rapport au réservoir .

Nous avons voulu mettre en lumière le fait qu’une représentation du temps logique est inévitable, et nous l’avons illustré par le fait que, l’ignorant dans son édifice théorique, Xenakis est toutefois obligé de s’en servir dans sa construction musicale. Le graphe harmonique donné plus-haut, appartient à la même espèce, bien qu’il ne constitue pas un préordre. Interprété soit comme un graphe soit comme un automate fini indéterministe, il propose une topologie du matériau qui légitime certains chemins et en exclut d’autres, et constitue donc une représentation minimale de la classe des séquences qu’il est possible de former sur les labels harmoniques. Or chacune de ces séquences peut encore admettre une infinité de réalisations en temps physique.

Il faut aussi insister sur le fait que les objets pris dans les réseaux du temps logique peuvent être et sont en général des objets abstraits, telles les étiquettes harmoniques et les réservoirs de nos exemples, susceptibles de dériver en des réalisations fort complexes sur la partition : ce n’est pas par hasard ; en effet, plus haute l’abstraction, plus lointaine et difficile sa résolution en une séquence terminale reperée dans le temps physique, et plus commode une représentation non déterministe des enchaînements temporels.

Du point de vue de la calculabilité, il est intéressant de comparer ces deux exemples. Celui de Xenakis est calculable par nature, puisque le graphe compositionnel est en même temps le programme qui le calcule ! Son implémentation est donc directe, et nous l’avons expérimenté dans notre environnement de Composition Assistée par Ordinateur, OpenMusic. Bien sûr ce cas, esthétiquement très spécifique, n’est pas généralisable, sauf peut être à l’école américaine de la musique dite algorithmique, dans laquelle la partition est le programme. Dans le cas du graphe harmonique, il nous faut implémenter une machinerie capable d’éxécuter un automate fini, ce qui n’est pas bien difficile.

Qu’en est il de problèmes musicaux d’un abord plus difficile? Eh bien il faut à toute force tenter de les réduire à des problèmes décidables ou, pour employer la terminologie des grammaires formelles, à des langages reconnaissables.

Marc Chemillier a adopté cette stratégie avec succès dans sa thèse de doctorat sur les structures algébriques en musique, pour une question réputée difficile : une machine peut-elle reconnaître si un texte musical est orthodoxe relativement à la théorie sérielle, et corollairement, peut elle énumérer des séquences polyphoniques obéissant aux canons de ce style ?

Tout d’abord, Chemillier se débarasse, lui aussi, du temps physique, en substituant aux notions communes de dates et de durées, l’idée qu’on peut ramener toute séquence musicale polyphonique à une suite de symboles, en introduisant dans le vocabulaire des hauteurs un symbole nul (qui n’est pas le mot vide) et un symbole de continuation A’ pour chaque hauteur A.

Ainsi la séquence

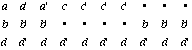
formée sur l’alphabet initial {a,b,c,d} étendu à A = {a,a’,b,b’,c,c’,d,d’,•}, puis à P =A), et qui peut encore se simplifier en :

si l’on ne considère que les attaques et que l’on ignore les silences. L’ensemble des séquences musicales représentables est le monoïde libre P*.

L’exemple donné par Chemillier est le début des Variations pour piano op. 27 de Webern :

v =

Soit la série u = mi fa do# mib do ré sol# la sib fa# sol si et û son miroir. Il existe une décomposition de v en deux mots v1 et v2 :

v1 =

v2 =

tels que v = v1 || v2, où || note la superposition, définie par :

w = u || v w[i] = u[i] v[i] pour i ¾ min (|u|,|v|) et w[i] = soit u[i] soit v[i] selon le plus long des deux mots.

L’existence d’unetelle décomposition v = v1 || v2, dans laquelle v1 et v2 déroulent sans faiblir la série u ou son miroir û, atteste de la sérialité de v. On généralise à v = v1 || v2 || … || vn. Les mots de la forme vi sont appellées formes sérielles. Appellons langage sériel l’ensemble L des séquences de P* sérielles pour une série u. Chemillier montre que L est reconnaissable selon les étapes suivantes :

1. l’ensemble F(u) des formes sérielles sur la série u est reconnaissable
2. l’ensemble F(u)°, résultant de la superposition itérée de F(u), sur lui même est reconnnaissable (théorème de Latteux)
3. L = F(u)°, donc L est reconnaissable

Il est à noter que le théorème de Latteux (la superposition itérée de parties reconnaissables est reconnaissable), qui est un résultat significatif de la théorie des langages, a été suscité par la formalisation de chemillier : il peut encore arriver que la musique soit utile aux mathématique…

Le théorème de Kleene permet d’affirmer que L, reconnaissable, est rationnel (engendré par les opérateur union, concaténation et *) et engendré par automate fini. De plus il existe une relation entre la structure des langages, la décidabilité d’un problème, la calculabilité d’une fonction, et la complexité algorithmique. Notamment (thèse de Turing-Church), il y a équivalence entre les langages décidés par une machine de Turing , récursifs, décidables, calculables, et soluble algorithmiquement (cette classe regroupant des problèmes P et NP).

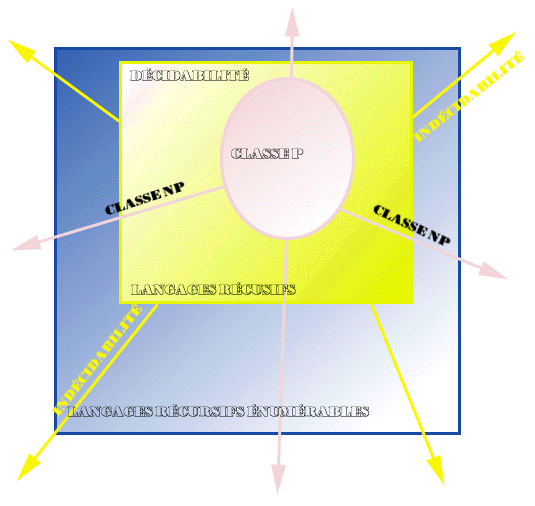
Le problème de la rationalité du langage sériel se situe selon nous à la frontière de P et de NP selon ce que l’on cherche précisément à calculer : si l’on a v1 et v2 et que l’on veut vérifier que v est sériel selon u, alors on a une procédure de calcul des automates associés et l’on est dans P. Si l’on dispose de v mais que l’on ne sait pas quelles séries sont concernées et en quel nombre, et que l’on cherche la décomposition sérielle minimale, alors il est possible que l’on soit dans NP, mais cette étude n’a pas été menée à notre connaissance.

Nous avons cependant mené une étude sur une autre famille de problèmes musicaux, clairement non polynomiaux, pour laquelle nous avons pu nous ramener, en relaxant certaines contraintes, à un problème polynomial.

L’idée générale est de proposer des outils informatiques permettant de refonder des systèmes harmoniques locaux en dehors de toute référence à la série ou à la tonalité, et dépendant des matériaux spécifiques choisis pour une œuvre donnée. Soit par exemple un ensemble d’aggrégats de hauteurs (nous n’utilisons pas, à dessein, le terme accord, pour éviter de supposer une structure à priori de ces objets). Considérons les comme les sommets d’un graphe totalement connecté et dont les arcs sont étiquetés par le résultat de l’application d’une fonction de distance quelconque entre les sommets. Définissons alors un " bon " parcours harmonique comme un chemin parcourant tous les sommets (chemin hamiltoninien) et minimisant la somme des distances. Si la fonction de distance choisie possède un corrélat perceptif pertinent, nous aurons bien calculé par ce procédé un ordonnancement des points harmoniques qui maximise telle ou telle forme d’euphonie. En choisissant des critères simples comme le nombre de notes communes, ou la relation commune à une fondamentale (éventuellement virtuelle), ou la ressemblance de textures, calculables à l’aide des procédés de Hindemith ou d’Estrada, ou encore le degré de ruguosité psycho-acoustique, l’expérience montre une assez bonne adhésion des auditeurs aux résultats du calcul. Notons en passant que cette technique du plus court chemin indexée sur le critère de notes communes est employée par Schönberg, citant Brückner, dans son traité d’harmonie, pour justifier les règles primitives d’enchaînement harmoniques.

Malheureusement, le problème ainsi formulé constitue un instance du fameux " voyageur de commerce ", connu pour être NP-Complet, ce dont les conséquences se font sentir très vite dès lors que l’on désire traiter un grand nombre d’objets musicaux. On décide alors de relâcher quelque peu la contrainte d’optimalité, et de rechercher un chemin dont le coût soit borné par une certaine fonction du coût optimal. Un théorème présenté par Rosenkranz, Stern & Lewis dans un article de 1977 détermine une méthode de construction qui garantit une borne supérieur égale à deux fois l’optimalité.

L’algorithme se déroule ainsi :

La complexité de l’étape 2 est en O(E logV) où E est le nombre d’arcs et V le nombre de sommets. La complexité de l’algorithme est en O(V²) car le graphe est totalement connecté.

La mauvaise nouvelle consiste en ce que, si les objets considérés, associés à la fonction de distance, ne respectent pas l’inégalité triangulaire, il est alors démontré (c’est le théorème de Sahni et Gonzales) qu’il ne peut exister d’algorithme polynomial borné pour le problème du voyageur de commerce, à moins que l’on puisse démontrer la conjecture P = NP. Vous savez qu’une fondation internationale, renouvelant récemment le programme de Hillbert, a inclus la demonstration de cette conjecture (ou de son contraire) dans la liste des défis mathématiques contemporains et a offert une somme considérable au vainqueur, ce qui montre que la recherche musicale n’est pas non plus complètement déconnectée des réalités économiques…

Parmi les critères donnés en exemple, certains ne respectent pas l’inégalité triangulaire. Il est amusant de constater que c’est pour l’un d’entre eux, le comptage des notes communes, que les résultats musicaux ont été le plus satisfaisants. Si l’on examine les séquences ainsi engendrées, on s’aperçoit que les résultats sont excellent sur des segments assez longs et contigus, séparés par des " catastrophes ", ce qui est tout à fait exploitable en effet, et a été exploité avec profit par plusieurs compositeurs. Une piste existe, issue de la recherche en statistique, consistant en la construction d’une hypermétrique à partir de notre pseudo métrique, qui nous permettrait de nous mettre en accord avec la théorie. Mais je dois confesser que les utilisateurs étaient si heureux de disposer de ce procédé que j’ai remis cette étude pour un futur improbable : c’est là, évidemment, la différence entre l’informatique et les mathématiques.

Aujourd’hui, beaucoup d’expériences sont menées sur des environnements d’informatique musicale basés sur le lambda-calcul (Orlarey), la logique du premier ordre (Rueda, Pachet, Roy, Courtot), la théorie des graphes (de Sainte-Catherine). En particulier, les systèmes à base de contraintes (CSP) sont d’un grand intérêt : ils permettent de considérer la texture musicale comme un espace discrétisé muni de relations potentielles de point à point. Essentiellement indéterministe, ces formalismes sont parfois appelés " structures musicales partiellement instanciées " dans la mesure où les descriptions mêlent des littéraux et des variables connectées par des relations (des contraintes) pouvant résulter en un grand nombre de réalisations qui respectent néanmoins les propriétés définies par le compositeur. C’est un changement de point de vue important dans la relation à l’outil informatique, car il ne s’agit plus de fournir les briques de bases et le calcul fonctionnel permettant de construire un objet déterminé, mais de raisonner sur des propriétés, et d’accepter éventuellement la surprise du résultat, surprise d’autant plus grande que le problème sera sous-contraint.

Ces questions sont difficiles à traiter : le problème général de la satisfaction de contraintes est NP-Complet, et les systèmes effectifs s’en sortent par la réduction à des sous-classes de problèmes musicaux et corollairement à des choix de représentation favorisant l’expression de ces sous-classes. Par conséquent les difficultés rencontrées sont toujours liées au manque de généralité et à la difficulté d’exprimer un problème différent des problèmes bien traités : par exemple l’harmonie contre le rythme, le tissu contrapuntique contre l’harmonie. Il y a là probablement un manque de concept unificateur des représentations musicales.

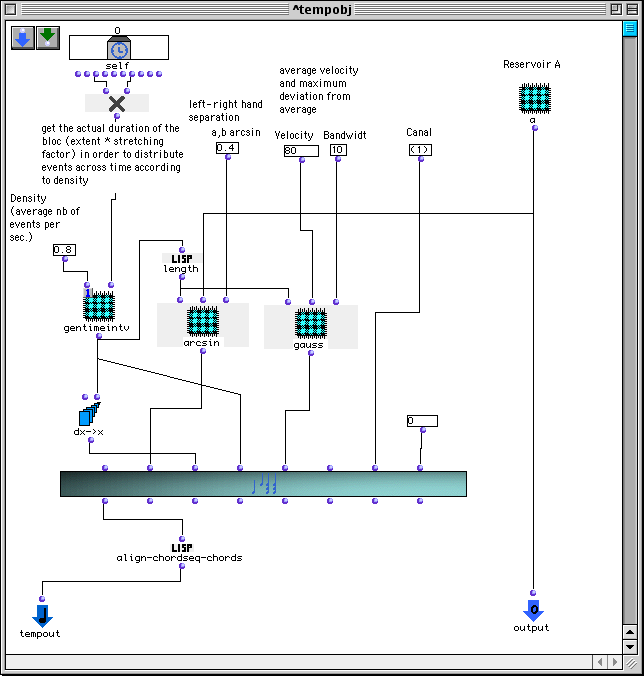
Pour terminer nous voudrions donner un aperçu d’un outil, nommé " maquette ", que nous avons proposé et qui autorise une coexistence pacifique entre représentation procédurale (la partie " calcul ", immergée) et représentation de surface de la musique, donne accès aussi bien à l’organisation hiérarchique de la forme, qu’à l’organisation séquentielle, et permette enfin d’exprimer la tripartition hors-temps / temps-logique / en-temps.

Ce sont là plusieurs logiques musicales qui s’interpénètrent, donnant diverses possibilités de reconfigurations orthogonales :

• Recombinaison au niveau de la forme : les blocs peuvent être réarrangés, dilatés ou compressés dans le temps et la hiérarchie peut être remodelée.

• Modification des relations fonctionnelles (les connexions) : ce sont alors les trajets des matériaux au sein de la pièce qui sont modifiés, sans changer l’organisation formelle.

• Modifications procédurales, c’est-à-dire changement de l’algorithmique sous-jacente aux blocs. L’allure formelle et les relations fonctionnelles sont conservées.

• Modification du matériau. La substance sonore peut ainsi être changée sans modifier le reste.

• Indexation temporelle : les coordonnées temporelles peuvent être des paramètres du calcul, imprimant ainsi une plus grande dynamicité à la mise en-temps.

Cela revient d’une certaine façon à  disposer des calculs dans le temps et dans les strates de l’organisation musicales, sans accroissement de complexité par rapport aux programmes traditionnels : bien que la variété des structures musicales ainsi exprimables soit assez grande, elles sont toutes réduites à un simple treillis d’opérateurs, et réductibles au lambda-calcul. Cela permet aussi d’envisager la partition comme constituant sa propre analyse : plusieurs pièces nouvelles ayant déjà été réalisées à l’aide de ces maquettes, il y aura peut être assez rapidement du grain à moudre pour les musicologues, en particulier ceux que le calcul ne rebute pas.