Gérard Assayag, Peter Hanappe, Carlos Agon, Joshua Fineberg
IRCAM
1 Place I.Stravinsky
75004 Paris
Résumé : Nous abordons ici le problème de la transcription automatique de la musique à partir de séquences calculées par ordinateur ou de signaux sonores enregistrés. Nous présentons un système de quantification des rythmes, puis nous raccordons ce dernier à des procédures d'analyse basées sur des représentation temps/fréquence, de manière à proposer une chaîne complète allant du son aux symboles.
0. Introduction
Lorsqu'on étudie le problème de la nature quantifiée -- donc catégorielle -- des termes élementaires du langage musical, nature indispensable à leur notation, il n'est pas inutile de faire un détour par le langage tout court, et notamment ses aspects phonétiques/phonologiques, qui ont donné lieu à beaucoup d'expériences envisagées selon l'angle de la catégorisation. Petitot-Cocorda [Petitot 85] décrit ce qu'il appelle, à la suite de René Thom, l' aporie fondatrice de la phonologie : "Comment un flux acoustique de nature physique et décrit par des formalismes de type analyse spectrale peut il devenir perceptuellement le support d'un code phonologique de nature linguistique et décrits par un formalisme de type algèbre discrète de traits distinctifs binaires?" Cette question se maintiendra en filigrane tout au long du présent article, puisque, on le verra au dernier chapitre, nous avons tenté, en partant d'un flux acoustique appréhendé selon son analyse temps/fréquence, de déployer des méthodes de quantification et de transcription qui nous conduisent jusqu'à la représentation de ce flux au sein d'un code (la notation musicale) qui se définit comme une combinatoire d'unités discrètes, associées aux catégories de la note, de l'intervalle, de la pulsation, du mètre.
Rappelons en quelques mots ce qu'est la perception catégorielle et la relation que met à jour Petitot-Cocorda entre cette dernière et la théorie des catastrophes de René Thom.
Le phénomène de perception catégorielle a été défini par Liberman en 1957 [Liberman 67]. Pour le mettre en évidence, on construit artificiellement entre deux stimuli A et B (e.g. deux couleurs, deux phonèmes) un "continuum" de stimuli en faisant varier un paramètre donné. Deux tests sont alors expérimentés : un test d'identification et un test de discrimination. Dans le test d'identification, après avoir choisi aléatoirement des stimulis parmi les éléments de la série interpolée, on demande au sujet de les ranger dans les catégories A ou B. Dans le test de discrimination, on présente des triplés XYZ où X est le stimulus n de la série interpolée entre A et B, Y est le stimulus n+1, et Z est toujours égal soit à X soit à Y. On demande alors si Z est égal à X ou à Y. Si la répartition des réponses est proche de 50/50 on en déduit que les sujets ne discriminent pas entre X et Y. S'il y a prédominance d'un type de réponse sur l'autre, les sujets discriminent. Les expériences sur la couleur ont montré que les sujets ont en général une bonne discrimination, à la fois fine (proximité des stimuli n et n+1) et constante (quelle que soit leur position dans la série) et identifient les nuances A et B indépendamment du choix des paires d'échantillons sur le trajet de A à B. En revanche, dans les expériences menées sur les phonèmes, on a constaté que la discrimination intra-catégorielle est très faible : dans la plus grande partie de la série interpolée, les sujets ne savent pas ranger les stimuli. La discrimination inter-catégorielle est, elle, de nature catastrophique : dans la région de la série qui se trouve à mi chemin de A et de B, la discrimination croît brutalement, atteint un maximum et décroît tout aussi brutalement ; le maximum est le point frontière (interface) où l'on bascule soudainement d'une perception de type A en une perception de type B. On parle alors de perception catégorielle.
Les caractéristiques de la perception catégorielle sont donc l'absence de discrimination intra-catégorielle et la discrimination inter-catégorielle catastrophique.
La discrimination est alors subordonnée à l'identification: les sujets ne discriminent que des phénomènes d'abord identifiés comme différents. La discrimination se fait sur des bases absolues et non pas relatives.
Petitot-Cocorda montre ensuite que la modélisation catastrophiste des phénomènes de morphogenèse et de différentiation opère une géométrisation de catégories taxinomiques-structurales auxquelles on n'accordait auparavant qu'un contenu logique. Elle permet de construire des espaces de contrôle dans lesquels les interfaces entre catégories apparaissent sous la forme de discontinuité de trajectoires.
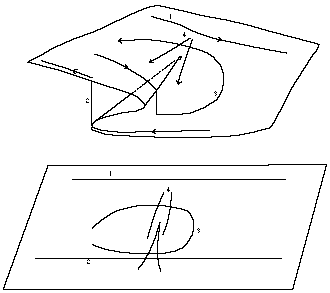
Soit S un système contrôlé par des paramètres de contrôle variant dans un espace de contrôle multidimensionnel W. Pour chaque variable w dans W, le système manifeste une qualité, une "couleur", qw. Lorsque w varie dans W, qw varie de manière continue ou discontinue. Il y a donc deux types de points de W : des points réguliers autour desquels la "couleur" varie continûment, et des points catastrophiques ou singuliers autour desquels la trajectoire saute d'une couleur à une autre. Dans la Figure 1 est représentée une des familles de catastrophes inventées par René Thom [Thom 80]. Des trajectoires types sont tracées dans cet espace paramétriques :
1. évolution lisse
2. transition catastrophique.
3. hystérésis
4. bifurcation

Figure 1. Catastrophe de type cusp d'après [Petitot 85] et [Thom 80]
Qu'en est il des unités du langage musical ? Nous aborderons la question de la quantification -- c'est à dire de la catégorisation -- et de la transcription des éléments musicaux selon les deux grandes catégories de la hauteur et de la durée.
Historiquement, deux phases sont identifiables [Assayag 1995].
La première, qui va en gros de Pythagore à Zarlino aboutit par tatonnements à un modèle où l'univers des sons à hauteur définie est ramené à une valeur de référence (qui deviendra plus tard le la 440). Des proportions de nombres entiers définissant les relations internes entre harmoniques de ce son sont formées puis ramenées à la fondamentale du même son pour construire une échelle. Le mécanisme est appliqué récursivement, des hauteurs issues de ce premier traitement étant à leur tour considérées comme fondamentales, leurs harmoniques analysées etc. La grille complexe issue de ce traitement est une sélection quantifiée du continuum sonore qui peut être déplacée dans son ensemble lorsqu'on change la référence initiale. Elle conserve alors sa structure interne, mais les grilles sont incompatibles entre elles, c'est à dire qu'elles ne sont pas stable pour la transposition.
Ce travers motive la seconde phase, soit l'émergence du tempérament égal au XVIIème siècle. Ici a lieu un deuxième type de quantification qui sort du champ des fractions rationnelles mais accède aux propriétés d'un système formel (Z/12Z) dont [Balzano 80] a montré le caractère optimal pour un certain nombre d'opérations musicales d'importance, notamment la transposition.
Du point de vue qui nous intéresse, il faut noter que la première phase, par son exploration puis son extériorisation des relations internes d'un son défini, met en lumière les aspects du monde sonore les plus susceptibles de donner lieu à perception catégorielle. En effet, il ne semble pas y avoir perception catégorielle dans le continuum des hauteurs, qui s'apparenterait plutôt aux couleurs de notre exemple précédent (on sait que des sons dont la hauteur est très proche, à quelques cents d'intervalle, seront perçus comme ayant non pas une hauteur mais une "couleur timbrale" différente, il reste qu'on les distinguera en tant que phénomènes). En revanche, il n'en va pas de même si l'on passe aux intervalles de hauteurs, et que l'on envisage ainsi des relations de relations.
Si l'on fait varier continûment la note supérieure d'une paire de notes formant un intervalle de tierce mineure de telle sorte que cet intervalle se déplace vers la tierce majeure, il y aura un point de basculement intercatégoriel. Siegel [Siegel 77] note que les musiciens entraînés ont une excellente identification, mais une plus mauvaise discrimination (i.e. ils sont plus categoriels) que les auditeurs non entraînés. Il existe aussi un apprentissage des categories.
Quant à la deuxième phase, celle du tempérament, G. Bloch remarque que son efficace réside peut être dans la réduction du nombre des catégories : une tierce majeure reste la même quelle que soit sa position dans l'échelle.
Ainsi le son musical, selon qu'on l'envisage comme continuum ou ensemble de relations de relations procède-t-il des deux grandes modalités de la perception définies par Liberman. Cela évoque le défi inhérent au style dit "mixte" en musique contemporaine, dans lequel coexistent une écriture pour instruments (écriture de notes) et de la synthèse artificielle de sons (navigation dans le continuum). Il est intéressant de constater que les oeuvres les plus abouties sont souvent celles où les deux domaines convergent : imitation par les instruments du champ continu (glissandi, bruit), contamination de la synthèse par les formalismes de l'écriture instrumentale (combinatoire d'unités identifiables).
3. Quantification dans le champ des durées
Un analogue du tempérament égal dans le domaine des durées est le striage régulier du temps dessiné par la pulsation périodique. Dans un cadre chromatique, une mélodie (dans une tessiture ramenée pour simplifier à une octave) peut être considérée comme une série toujours croissante (modulo 12) d'indices sur le cercle chromatique. Un rythme peut être considéré de même comme une série croissante d'indices sur un cercle dont chaque graduation représente une occurence de la pulsation unité et dont le nombre de graduation dépend de la périodicité de carrure choisie. Cette vision simplifiée suppose évidemment que l'on ne fait pas usage de valeurs rythmiques inférieures (e.g. un triolet) à la pulsation unité (e.g. la croche).
Une vision plus complète est donnée dans [Nicolas 90]. "le tempo peut être vu comme une hiérarchie qui agit simultanément sur trois niveaux emboités. Cette hiérarchie est le coeur de l'organisation mesurée qui permet de distinguer -- en allant de la durée la plus vaste à la plus restreinte -- le niveau de la mesure, celui de la pulsation et celui de l'impulsion". Il n'est alors plus possible de se ramener à l'analogue simplificateur de l'échelle, sauf à opérer un changement d'unité par un facteur égal au plus petit commun multiple de toutes les vitesses d'impulsions (facteur qui serait par exemple 60 si l'on devait considérer, sous la noire, la croche, le triolet, la double croche et le quintolet).
Il nous semble plus raisonnable de considérer que, si la même dynamique de quantification est à l'oeuvre dans la constitution des échelles de hauteur et dans celle du mètre, cette quantification est beaucoup plus mobile dans le deuxième cas en ce qu'elle réajuste sans cesse ses quanta, cette variété étant fondamentalement constitutive du rythme, alors que la variété mélodico-harmonique s'appuie, elle, sur une graduation figée (dans une même pièce tout au moins, et en excluant le cas, rare, de pièces à tempéraments multiples).
On comprend mieux dans ce cas pourquoi la transcription des durées est beaucoup plus complexe que celle des hauteurs. Il suffit pour cette dernière de préciser le tempérament de référence et d'effectuer un calcul trivial d'arrondi. Il faut pour la première reconstituer une hiérarchie métrique en évaluant à chaque niveau et à chaque instant le meilleur choix possible parmi des "tempéraments" multiples. De plus, les solutions n'étant pas uniques, une certaine formalisation des connaissances et de l'expérience musicale est indispensable.
Le projet de quantification et de transcription rythmique "Kant" mené à l'Ircam tente de proposer des solutions à ce problème.
En observant les quantificateurs intégrés dans les logiciels séquenceurs ou d'édition de partition disponible sur le marché, on constate assez vite un certain nombre de limitations qui les rendent inutilisable dans un contexte de production musicale trop éloigné de leurs hypothèses de base. Premièrement, les modèles sous-jacents supposent que les séquences à quantifier se disposent naturellement au sein d'une carrure périodique, traversée par une pulsation tout aussi régulière. Deuxièmement, ils supposent en général que cette carrure et cette pulsation prééxistent dans une partition de référence, absente, qu'il s'agit de retrouver par déduction. C'est certes le cas lorsqu'on cherche à transcrire une pièce de Bach ou de Mozart interprétée sur un clavier : certains éléments du jeu doivent être interprétés comme des déviations relativement à la structure temporelle de référence, déviations dues à des variations expressives volontaires ou involontaires. Dans le cas d'une utilisation créative pour la composition, le problème est différent : la notion de variation expressive est absurde concernant des matériaux calculés ou déduits par analyse de la micro-structure du son. De plus, bien que comportant en général une phase analytique, la démarche est de production plutôt que d'investigation : il ne s'agit pas de reconstituer une partition prééxistante mais d'en construire une inédite. Les critères ne sont pas de fidélité, mais de consistance et de minimalité de la notation. En particulier, des séquences proches d'un point de vue perceptif doivent être proches d'un point de vue notationnel, ce qui est moins simple qu'il n'y paraît. En effet, le déphasage des diverses occurences d'une même figure rythmique (ou de ses variations) par rapport à la grille de la pulsation conduit en général au résultat inverse, à savoir que des formes très proches sont transcrites par des combinaisons de signes très différentes.
L'hypothèse de départ du logiciel "Kant" est donc que le matériau avant quantification est porteur de formes, et ce sont ces formes qui feront l'objet d'investigations. Des méthodes d'analyse dont nous parlerons plus loin sont proposées pour découvrir les traits de structure saillants du point de vue perceptif, ces traits déterminant dans le flux temporel des points d'articulation, et, entre ces points, des segments pertinents. Le découpage métrique et le choix de la pulsation sont déduits de la morphologie des segments. Finalement, les segments, et par conséquent les évènements élémentaires qu'ils incluent, sont soumis indépendamment les uns des autres à un étirement ou une compression temporelle qui garantit leur alignement avec la grille de la pulsation. De ce fait, deux segments porteurs d'une même figuration rythmique bénéficient du même alignement sur la grille de pulsation, ce qui facilitera considérablement leur transcription ultérieure en des expressions identiques. Ce dernier point est important et peut être justifié de la manière suivante : plutôt que d'avoir une erreur de quantification distribuée aléatoirement au sein de la micro structure rythmique -- ce qui provoque en général et le défaut de cohérence et le défaut de minimalité -- cette erreur est localisée et donc à la fois contrôlée et bornée au niveau des segments.
Nous avons indiqué que la pulsation est déduite de la morphologie des segments : les expérimentations menées à cette fin dans le cadre du projet devaient délivrer une surprise intéressante. En effet, les meilleurs résultats furent obtenus en appliquant une technique qui avait fait ses preuves non pas dans le champ des durées mais dans celui des hauteurs, ce qui renforce encore le sentiment d'analogie exprimé plus haut. Il s'agit de l'algorithme de détection de fondamentale virtuelle. Cette dernière est une fréquence grave, non obligatoirement présente dans le spectre des fréquences d'un son, et qui, multipliée par des coefficients entiers, engendre tous les partiels de ce son, à une approximation près. Lorsqu'on se place dans un cadre tempéré (fondamentale virtuelle d'un accord), cette approximation est définie par l'intervalle unité du tempérament choisi (e.g. un quart de ton). Ainsi chaque note de l'accord peut être appariée avec une "harmonique" de la fondamentale, sans lui être tout à fait égale, mais se ramenant tout de même par quantification au même degré de l'échelle définie par le tempérament. Voir [Terhardt 82] et [Assayag 86].
Ce calcul a été beaucoup utilisé ces dernières années par des compositeurs qui s'en servent pour harmoniser des complexes sonores divers relativement à un même spectre harmonique de référence.
Pour comprendre la nature de ce "transfert de concept" que nous opérons entre champ des hauteurs et champs des durées, il faut considérer la série des durées des segments temporels successifs comme une sorte de spectre (où les durées remplacent les fréquences). La "fondamentale virtuelle" de ce spectre est donc une durée constituant un diviseur commun approximé à tous ces segments, qui peut alors être proposée comme durée unité, c'est à dire comme pulsation. Notons que Stockhausen, avec ses "formants" rythmiques avait eu une intuition très proche de cette communauté d'organisation entre champs des hauteurs et champs des durées [Stokhausen 88].
Nous utilisons non pas un mais deux facteurs d'approximation (nous n'entrerons pas dans le détail dans le cadre de cet article, la description complète du processus est donnée dans [Assayag 94]) qui déterminent un plan paramétrique, dans lequel s'opére, là aussi, une catégorisation : dans cet espace apparaissent des "quantal regions" [Petitot 85] à chacune desquelles est associée une et une seule pulsation et qui sont séparées par des frontières catastrophique. Lorsque les facteurs d'approximation varient continûment, la valeur de pulsation approximée reste constante ou change brusquement de palier lorsqu'une frontière de région est traversée.
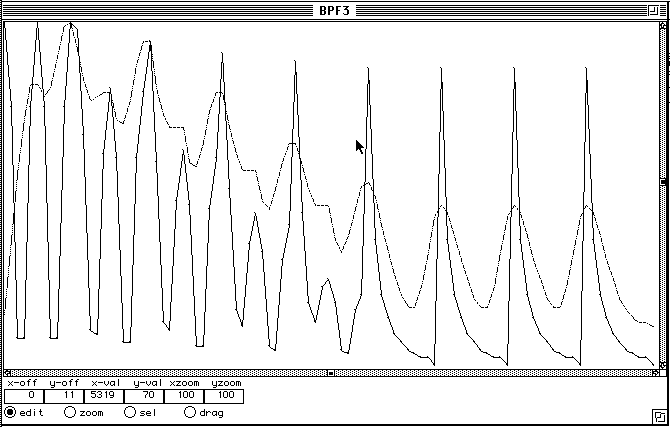
Figure 2. Interpolation rythmique, Tristan Murail. Représentation évènement / durée.

Figure 3. Interpolation rythmique. Quantification traditionnelle.
On introduit donc dans la quantification rythmique un niveau intermédiaire de la hiérarchie métrique, une segmentation en gros équivalente au découpage en mesures, permettant de contrôler localement le bruit de quantification. Reste à déterminer les critères de cette segmentation. Précisons tout d'abord que nous avons voulu donner au musicien le contrôle total de cette phase critique du traitement : le programme est conçu comme un éditeur graphique et interactif permettant d'effectuer manuellement le découpage d'une séquence. Mais il propose tout de même un ensemble de stratégies de segmentation automatique combinables entre elles et avec le découpage manuel.
Parmi ces méthodes, deux se sont avérées efficaces dans le cas de séquence de durées engendrées par des modèles simulant des processus physiques. La première est basée sur la détection de "pics" de durées, soit des durées plus longues que celles qui précèdent et qui suivent. Par lissage du graphe exprimant les durées en fonction du numéro d'évènement, on ne retiendra que les pics les plus significatifs, c'est à dire qu'on comparera chaque valeur de durée avec une moyenne des durées environnantes sur un voisinage plus ou moins large. Le critère perceptif pertinent ici est l'accent agogique : en segmentant aux positions de ces accents, on aligne ces derniers avec la pulsation, évitant ainsi qu'ils n'apparaissent au milieu d'une figure compliquée. La seconde méthode est fondée sur la courbe de densité obtenue en déplaçant le long de la séquence à quantifier une fenêtre temporelle constante dans laquelle on calcule une valeur de densité fonction du nombre d'évènements présents. L'étude de cette courbe permet de détecter des groupements d'évènements rapprochés dans le temps qui tendent à être nettement isolés par la perception de leur contexte passé et futur. D'autres méthodes sont basées sur la reconnaissance de formes (patterns de durées) avec approximation ou de quasi-synchronismes dans le cas de séquences polyphoniques.
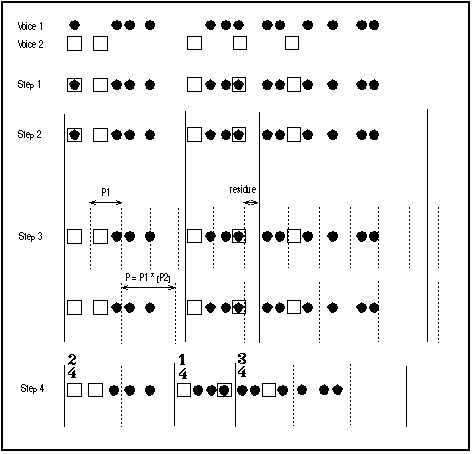
Figure 4. Les étapes de l'analyse dans Kant.
L'approche du rythme sous-entendue dans le modèle "Kant" implique la considération du phénomène sonore de référence comme une boîte noire sur laquelle on dispose de peu de connaissance. Elle est particulièrement justifiée dans le cas de phénomènes complexes, notamment chaotiques, sur lesquels l'imposition d'une pulsation arbitraire est dénuée de sens, et cause en général l'échec des quantificateurs traditionnels. Plutôt que de considérer le phénomène comme une surface sur laquelle on tracera une grille de quantification, nous effectuons un détour par un modèle de perception impliquant l'aggrégation de phénomènes élémentaires en objets de plus haut niveau (que nous avons appelé segments), ce qui impose un premier niveau de structuration des données avant leur quantification. Ce sont, dans une première phase, ces objets qui seront cadrés, au prix d'une déformation, dans une pulsation (puisque la contrainte que nous nous donnons est malgré tout la transcription dans un système de notation métrique) et non pas les évènements sonores élémentaires. Ces derniers le sont à leur tour dans une deuxième phase du traitement. C'est cette pré-structuration qui assure la propriété de cohérence (même phénomène, même notation). Bien sûr plusieurs segmentations sont possibles selon les structures que l'on veut mettre en évidence : c'est là un des principaux degrés de liberté du système.
Kant a été implémenté par G.Assayag et C. Agon et a bénéficié de l'expertise musicale de J. Fineberg [Agon 94] [Assayag 94].
Le graphe figure 2 montre une représentation évènement/durée d'un processus rythmique dû à Tristan Murail et obtenu par une interpolation continue entre une sinusoïde (accélération et décélération périodique) et une exponentielle (accelerando). L'accelerando, une fois atteint, est répété trois fois. Entre la sinusoïde et l'exponentielle, la zone intermédiaire de l'interpolation a un caractère d'instabilité très perceptible. Les pics de durée dénotent des évènements longs (agogiques) environnés d'évènements plus courts. La courbe lissée permet de sélectionner les agogiques les plus marquants (figure 2).
Dans la figure 3, la quantification de cette séquence par l'approche traditionnelle (métrique et pulsation arbitraires) montre le défaut de cohérence (l'accelerando est noté quatre fois de manière différente) et de simplicité (sans commentaire).
La figure 4 résume le traitement spécifique à Kant. Les ronds et les carrés représentent les débuts d'évènements élémentaires. Dans le cas polyphonique, les voix sont d'abord fusionnées (step 1). Puis les segments sont calculés ou donnés par l'utilisateur (step 2). L'algorithme de fondamentale virtuelle extrait une pulsation (step 3, trait pointillé). Les segments sont dilatés ou compressés pour s'aligner sur la pulsation (step 4). Le reste du traitement, non figuré ici, consiste à disposer les évènements à l'intérieur de la pulsation en calculant des subdivisions (croche, triolet etc.) optimales de cette dernière.
Le résultat est présenté sous la forme d'une partition rythmique. On note que des phénomènes identiques sont représentés de manière identiques, que le caractère symétrique de la sinusoïde est bien matérialisé par la structure miroir des trois premières mesures. Dans la partie centrale, instable du point de vue rythmique, les phénomènes de symétries et de répétitions avec déformation sont bien notés. La simplicité est acceptable compte tenu du caractère irrégulier du phénomène analysé (figure 5).

Figure 5. Interpolation rythmique. Quantification avec Kant.
5. Du signal aux symboles
Nous avons montré dans les paragraphes précédents comment l'on pouvait quantifier et transcrire des ensembles de valeurs, fréquences ou durées supposées données. Cette phase étant assurée, nous avons essayé de compléter la chaîne d'analyse en la faisant redescendre jusqu'au son lui même, créant une passerelle entre le domaine du son et le domaine symbolique de la partition. Nous sommes partis de deux logiciels existants à l'Ircam, Audiosculpt et PatchWork. PatchWork est un logiciel écrit en CommonLisp qui manipule des structures musicales symbolique et qui est utilisé comme environnement pour la composition assisté par ordinateur (CAO). PatchWork possède une interface graphique de programmation visuelle et un ensemble d'éditeurs spécialisés dans la représentation et la manipulation de partitions musicales. AudioSculpt est un logiciel d'analyse et de synthèse des sons. Il possède une interface graphique servant à visualiser et manipuler les analyses notamment sous la forme de sonagrammes.
L'idée consiste à analyser des sons dans AudioSculpt pour en extraire une représentation symbolique qui sera envoyée vers PatchWork, puis traitée dans Kant (Kant est un module de PatchWork).
Précisons encore une fois que notre but n'est pas la reconstitution d'une partition existante. En effet, nous nous situons dans un cadre de production et de composition dans lequel on suppose que le musicien, partant d'un signal sonore (enregistrement, signal synthétisé) dont il désire se servir comme matériau générateur, va, à l'aide d'un ensemble de procédures combinant automatisme et interaction, en extraire des informations musicales "nécessaires et suffisantes" pour constituer une trame mélodique, harmonique, rythmique et dynamique, représentable dans le cadre de la notation instrumentale. Dans ce contexte, une description partielle du son peut suffire si les paramètres extraits sont pertinents au regard de la perception.
Dans le flux du signal sonore, des régions considérées comme significatives vont donc être isolées et extraites. Régions temporelles : il s'agit de segments du son perçus comme des événements. Régions spectrales : il s'agit de sous ensemble de partiels, allant de la fondamentale (si cela a un sens dans le cas du son analysé) jusqu'à des sous ensembles de partiels considérés comme significatifs du point de vue de la couleur harmonique du son. Ces partiels ont eux même une composante temporelle et énergétique et seront donc constitués comme objets dotés d'attributs. Les critères qui permettent de juger de ce qui est ou n'est pas significatif intègrent évidemment des éléments subjectifs : d'où l'importance capitale de fournir au compositeur un interface de sélection et d'édition des objets (segments, partiels) issus de l'analyse.
Cette démarche visant à quantifier un processus sonore et à le réintroduire ainsi dans l'univers de l'écriture musicale est largement pratiquée par les compositeurs depuis une vingtaine d'année (citons par exemple Tristan Murail, Gérard Grisey, Joshua Fineberg, Claudy Malherbe, Georges Benjamin, Kaija Saariaho, Marco Stroppa, Hugues Dufour). Messiaen en fut un pionnier avec ses transcriptions de chants d'oiseaux. François Bernard Mâche [Mâche 90] fut probablement le premier, dès les années soixante, à utiliser la technologie électronique et numérique pour transcrire des enregistrements sonores en partitions, à partir de sonagrammes.
Il est intéressant de noter que cette technique reproduit localement (i.e. à l'échelle d'un processus sonore spécifique, éventuellement inharmonique) le mécanisme plus général de discrétisation, de réduction et d'abstraction de l'univers sonore (réduit auparavant aux phénomènes purement harmoniques) qui a progressivement contribué à former les systèmes d'échelles de l'écriture musicale occidentale.
Les paramètres musicaux qui sont visés comme les plus importants sont:
* le temps: dates de début des événements significatifs ou des partiels sélectionnés.
* la fréquence: valeur en fréquence des sous ensembles de partiels sélectionnés.
* intensité: rapports d'intensité des partiels sélectionnés afin de pouvoir reconstituer une dynamique ou un timbre.
Parmi les applications de ce projet, notons l'intégration de
matériaux sonores exogènes dans l'écriture musicale
instrumentale, notamment la possibilité de déterminer des "points
d'accroche" musicaux (hauteurs, durées, intensités) pour
l'articulation fine entre instruments et sons concrets ou
synthétisés. D'autres applications peuvent être
proposées dans le
domaine de l'ethnomusicologie (transcription
d'enregistrements en notation traditionnelle aux fins d'en analyser les
échelles et le rythme) et transcription de musiques
électroacoustiques (aux fins de constituer, sous la forme de la
partition, un support visuel à l'écoute)
5.1 Symbolique / subsymbolique
Peter Hanappe [Hanappe 95] rappelle l'opposition symbolique /subsymbolique qui nous sera utile pour expliciter les phases successives d'analyse dans Audiosculpt et PatchWork.
Nous appelons symbolique, à la suite de [Camurri 94] tout système de représentation dans lequel les "atomes" sont eux même des représentations, c'est à dire qu'ils sont dotés d'une signification élémentaire et qu'ils ont un rôle syntaxique élémentaire au sein d'une organisation plus vaste. Ainsi de la note, qui désigne une unité musicale clairement définie. Dans le domaine symbolique nous trouvons les notes, les accords, les figures rythmiques élémentaires etc.
Nous appelons sub-symbolique tout système de représentation dans lequel les atomes ne sont pas des représentations. C'est le cas, par exemple, de la représentation sonagraphique dans laquelle les unité élémentaires (les "pixels") n'ont de signification qu'une fois pris dans une organisation supérieure (e.g. un ensemble de pixels formant un partiel).
De ce point de vue, nous voulons créer une passerelle qui permet de passer d'un environnement sub-symbolique à un environnement symbolique.
5.2 Représentations temps/fré-quence
Un sonagramme est la représentation en deux dimensions d'une "surface" dans un espace tridimensionnel dans lequel la première dimension représente le temps, la deuxième dimension la fréquence et la troisième dimension l'amplitude. On utilise généralement la transformation de Fourier pour la construction de cette "surface".
Cette surface étant traitée numériquement, elle est discrétisée à la fois dans le domaine temporel et dans le domaine fréquentiel. Les "pixels" pris dans ces deux domaines (trames d'analyse constituées de bandes fréquentielles) sont sub-symboliques. Un premier niveau de regroupement "pré-symbolique" consiste à tracer les lignes de crêtes sur la surface sonagraphique : c'est le suivi de partiels. Un autre type de construction pré-symbolique est la segmentation le long de l'axe temporels d'unités dont le début est déterminé par des déplacements brusques d'énergie : c'est la reconnaissance d'évènements. Ces deux élaborations pré-symboliques se font dans AudioSculpt. Les données sont ensuite envoyées à PatchWork qui se consacre à les transformer en représentations symboliques : les évènements deviennent des notes ou des accords, les configurations de partiels déterminent le contenu harmonique, enfin, les configuration de dates et de durées dans le domaine temporel deviennent en passant dans Kant une écriture rythmique.
La phase "pré-symbolique" se déroule selon deux modalités possibles.
Dans la première nous modélisons le son comme une suite d'unités sonores distinctes, chaque unité commençant à la fin de la précédente.Pour chaque unité, un suivi de partiel local au segment temporel considéré délivre une collection de hauteurs qui sera plus tard interprétée comme un accord dans PatchWork. Nous appelons cela : représentation en suite d'accords.
Dans la seconde, le son est considéré dans sa globalité et le suivi de partiels détermine les naissances et les morts d'unités de fréquence pré-symboliques où qu'elles arrivent dans le son. Cette analyse débouche sur une configuration temps/fréquence complexe qui se rapproche de la notion de polyphonie et dans laquelle l'idée d'événement devient plus lâche, notamment s'il s'agit de trames sonores très continues. Nous appelons cette analyse le suivi de partiels.
La technique d'analyse de base est le vocodeur de phases qui opère une transformation de Fourier à court-terme (TFCT) glissante sur le signal sonore [Moorer 78]. Le vocodeur implémenté dans Audiosculpt est Super Vocodeur de Phase de Philippe Depalle. Nous rappelons l'équation
S(k, q) =
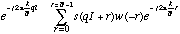
avec
s(n): le n-ième échantillon du signal
w(n): fenêtre de pondération (Hanning, Hamming ou Blackman)
N: taille en nombre d'échantillons de la FFT
I: le pas d'avancement
q: l'indice du temps
k: l'indice des fréquences
L'indice k représente la dimension de fréquence, l'indice q représente la dimension de temps. S(k, q) est un nombre complexe. Fe est la fréquence d'échantillonnage. Les fréquences discrètes de l'analyse sont données par k.Fe / N. Les valeurs discrètes du temps sont données par q.I / Fe.
5.3 Suite d'accords
Dans ce mode d'analyse, nous cherchons les endroits où un déplacement d'energie assez important se manifeste dans le spectre. Ces changements d'énergie sont calculés par la différence de deux trames d'analyse consécutives (dérivée du spectre):
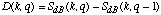
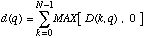
De manière à minimiser les variations locales, le spectre S(k, q) est moyenné sur cinq trames consécutives. De plus, la dérivée d(q) est normalisée en la divisant par l'énergie à l'instant q :
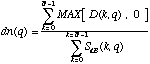
La dérivée dn(q) peut êter considérée comme une mesure de distance entre deux spectres consécutifs et l'arrivée d'un événement est repérée comme un maxima dans cette fonction de distance. Les positions temporelles auxquelles dn(q) est supérieur à un seuil spécifié sont repérées et des marqueurs graphiques sont alors ajoutés à ces positions. L'utilisateur peut éditer ces marqueurs (en les déplaçant ou en les effaçant).
Une fois les positions temporelles détectées, la structure fréquentielle de chaque segment est analysée localement à ce segment, selon la procédure générale de suivi de partiels décrite ci-après.
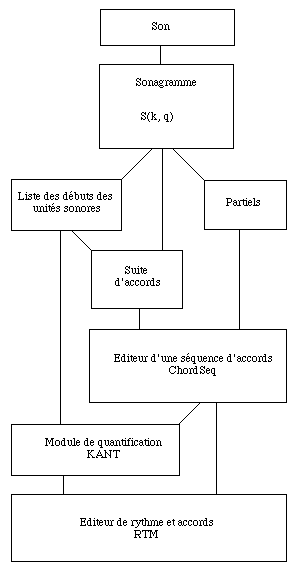
Figure 6. Quantification et transcription dans Audiosculpt et PatchWork.
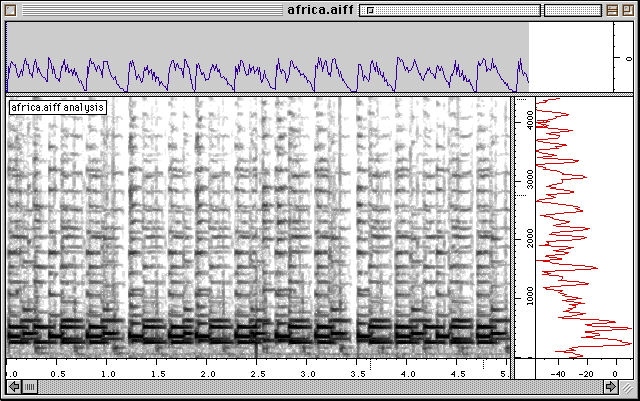
Figure 7 Sonagramme

Figure 8 Sonagramme contrasté
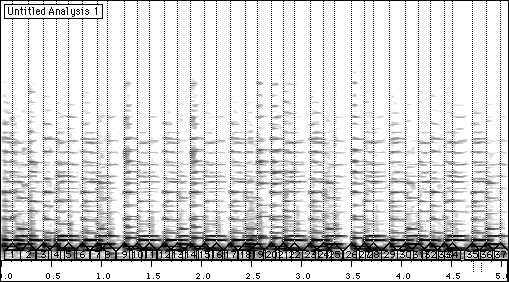
Figure 9 Détection d'évènements et segmentation.
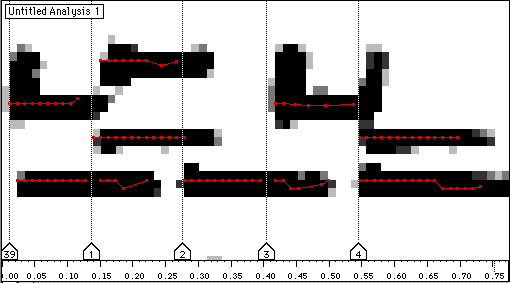
Figure 10 (Grossissement) Détection des partiels à l'intérieur des segments.
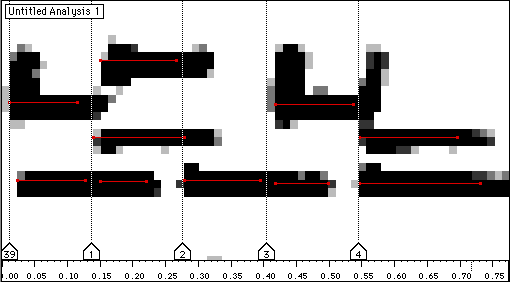
Figure 11 Moyennage des partiels.
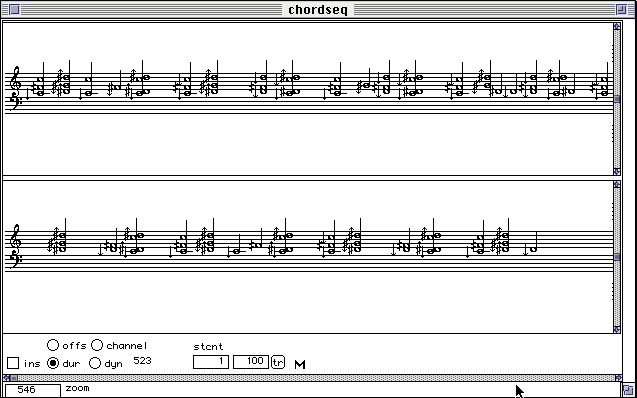
Figure 12 Interprétations des données d'analyse dans PatchWork. Quantification des hauteurs dans une grille de 1/8ème de ton.
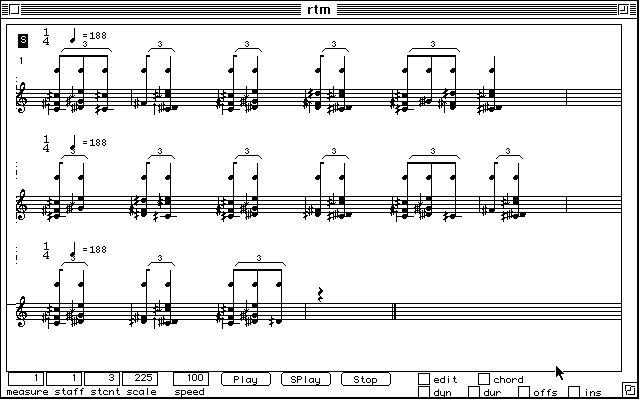
Figure 13 Quantification des durées et transcription complète à l'aide du module Kant.
5.4 Suivi de partiels
Le sonagramme est d'abord réduit en seuillant à 0 toutes les amplitudes plus petites qu'une valeur réglée par l'utilisateur grâce à un contrôle de contraste qui lui donne un feed-back visuel instantané. Puis les pics d'amplitude sont détectés dans chaque trame d'analyse.
Soient F(n,t), n = 1, ..., N, les fréquences des pics détectés dans le spectre à l'instant t, et F(m,t - 1), m = 1 , ... , M, les fréquences des pics dans le spectre à l'instant t - 1.
Nous définissons une mesure de distance:
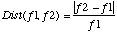
et une distance maximale DMAX destinée à limiter les trop grands sauts en fréquence.
La connexion entre les pics du spectre S(t-1) avec les pics du spectre S(t) est faite comme décrit ci-dessous. A chaque fois nous partons du spectre qui a le moins de pics (S(t) ou S(t-1)). Les connections sont faites en évitant que deux partiels se rejoignent ou au contraire qu'un partiel se divise en deux. Les pics ne peuvent alors être attribués qu'à un seul partiel.
Si M > N, il y plus d' "anciens" pics que de "nouveaux" pics. Les connections sont cherchées à partir de S(t).
* Pour chaque pic F(n, t) de S(t) nous cherchons le pic F(j, t-1) de S(t-1), pour lequel Dist(F(n,t), F(j, t-1)) est minimale.
* Si la distance minimale est plus que petite que DMAX, on regarde si le pic F(j, t-1) n'a pas encore été connecté avec un pic F(i,t), i!=n. Ainsi nous évitons qu'un partiel se divise en deux. Si en effet le pic trouvé F(j, t-1) a déjà été connecté avec un pic F(i,t), i!=n, on connecte F(j, t-1) avec le pic (F(i,t) ou F(n,t)) pour lequel la distance est la plus petite.
* Si la distance minimale est plus grande que DMAX la connexion entre F(n,t) et F(j, t-1) n'est pas établie.
* Les fréquences F(n,t) qui ne sont pas connectées commencent des nouveaux partiels. Les fréquences F(m,t-1) qui ne sont pas connectées terminent des partiels.
Le traitement se déduit aisément pour N > M.
La séquence des traitements est résumée dans la figure 6.
Les extensions d'Audiosculpt pour la segmentation et le suivi de partiels ont été programmées par Peter Hanappe [Hanappe 94] dans le cadre de son DEA (direction G. Assayag) et ont bénéficié de l'expertise musicale de J. Fineberg, C. Malherbe. et T. Murail.
5.5 Un exemple
Nous avons analysé et transcrit un échantillon de musique pour harpe du peuple Nzagara de Centrafrique, enregistré par Marc Chemillier [Chemillier 95]. Les étapes successives de la quantification et de la transcription sont données dans les figures 7 à 13.
[Agon 94] Agon, A. KANT: Une critique de la quantification pure, Mémoire de DEA Informatique, Université de Paris XI, 1994.
[Assayag 86] Assayag G., Castellengo M., Malherbe C. Functional Integration of Complex Instrumental Sounds in Music Writing, Proceedings of the ICMC, Den Haag, 1986.
[Assayag 93] Assayag G., Rueda C. The music representation project at Ircam, Proceedings of the ICMC, 1993, Tokyo, Japan.
[Assayag 94] Assayag, G., Agon, C., Fineberg, J., Rueda, C. Kant: a Critique of Pure Quantification, Proceedings of the ICMC, Aarhus, 1994.
[Assayag 95] Assayag A., Cholleton J.P. Musique, nombres et ordinateurs, La recherche ndeg. 278, Paris, Juillet/Août 1995.
[Balzano 80] Balzano, Gerald J, The Group-theoretic Description of 12-Fold and microtonal Pitch Systems, Computer Music Journal, vol 4, ndeg.4, pp 66-84, 1980.
[Brown 92] Brown, G.J., (1992), Computational auditory scene analysis: a representational approach, TR CS-92-22, University of Sheffield: Department of Computing Science
[Brown 93] Brown J.C, Determination of the meter of musical score by autocorrelation, J.Acoust.Soc.Am. 94. 1953-1957. (1993)
[Camurri 94] Camurri, Frixione & Innocenti, A cognitive model and a knowledge system for music and multimedia, Journal of New Music Research, 23(4), December 1994, p317-347.
[Cerveau 94] Cerveau, L., (1994), Segmentation de phrases musicales à partir de la fréquence fondamentale, Mémoire DEA ATIAM, Paris VI
[Chafe 82] Chafe, Mont-reynaud & Rush, (1982), Towards an intelligent editor of digital audio: recognition of musical constructs, Computer Music Journal, 6(1), p42-51, Spring 1982, Mass. Inst. of Techn.
[Chemillier 95] Chemillier M. Ethnomusico-logie et informatique. Bull. de l'AFIA. ndeg.23.pp 44-45. 1995.
[Chemillier 95] Chemillier M. La musique de la harpe. in Une esthétique perdue. Dampierre ed. Presse de l'ENS. Paris. 1995
[Desain 91] P. Desain, H. Honing, "The Quantization Problem : Traditional and Connectionist Approaches", in M. Balaban, K. Ebcioglu & O. Laske (Eds) Understanding Music with AI : Perspectives on Music Cognition, pp 448-463, The AAAI Press, 1992.
[Eckel 92] Eckel, G, (1992), Manipulation of sound signals based on graphical representation: A musical point of view, Proceedings of the 1992 Int. Workshop on Models and Representations of Musical Signals, Capri, 5-7 October, 1992
[Entretemps 89]. La musique Spectrale. Entretemps No 8, sept. 1989.
[Hanappe 95] Hanappe P. Intégration des représentations temps/fréquence et des représentations musicales symboliques, Mémoire DEA ATIAM, Ircam/Paris VI, 1995.
[Krimphoff] Krimphoff, McAdams & Winsberg, (1994), Caractérisation du timbre des sons complexes. II. Analyses acoustiques et quantification psychophysique, Journal de Physique, 4(C5), Les Editions de Physique, Les Ulis, 1994.
[Lepain] Lepain Ph. & André-Obrecht R., (1995), Micro-segmentation d'enregistrements musicaux, Deuxièmes Journées d'Informatique Musicale JIM, LAFORIA, Inst. Blaise Pascal, Avril 7-8, 1995, Paris
[Liberman 67] A.M. Liberman, F.S. Cooper, D.P. Shankweiler, M. Studdert-Kennedy, Perception of the speech code, in Psychological review, 74, 6, pp 431-461 (1967)
[Mâche 90] Mâche, François-Bernard, Musique, mythe, nature ou les dauphins d'Arion, Klinksiek, Paris, 1990 [1ére édition 1983]
[McAdams 95] McAdams, St., Audition: physiologie, perception et cognition, dans "Traité de psychologie expérimentale 1", ed. Richelle, Requin & Robert, Presses Universitaire de France.
[Miranda 93] Miranda, E.R., (1993), From symbols to sound: Artificial intelligence investigation of sound synthesis., DAI Research Paper No. 640, Dept. of AI, University of Edinburgh, UK.
[Moorer 77] Moorer, J., (1977), On the transciption of musical sound by computer, Computer Music Journal, November 1977, p32-38, Mass. Inst. of Techn.
[Moorer 78] Moorer, J., (1978), The use of the phase vocoder in computer music applications, Journal of The Audio Engineering Society, 26(1/2): 42-45.
[Nicolas 90] Nicolas, François, Le feuilleté du tempo, Entretemps ndeg.9, 1990.
[Petitot-Cocorda 85] Petitot-Cocorda, Jean, Les catastrophes de la parole, Maloine, Paris, 1985
[Piszczalski 77] Piszczalski & Galler, (1977), Automatic music transcription, Computer Music Journal, November 1977, p24-31, Mass. Inst. of Techn.
[Siegel 77] Siegel, J.A. & W. Categorical Perception of Tonal Intervals. Perception and PsychPhysics, 21, 5, 1977.
[Stokhausen 88] Stokhausen, K. Comment passe le temps, Contrechamps ndeg.9, 1988. (Article original : Wie die zeit wergeht, Die Reihe 3, 1957)
[Terhardt 82] Terhardt, Stoll & Seewann, (1982), Algorithm for extraction of pitch and pitch salience from complex signals, J. Acoust. Soc. Am., 71(3), p679-688, March 1982, Acoust. Soc. of America
[Thom 80] R. Thom, Modèles Mathématiques de la morphogenèse. Christian Bourgois. Paris, 1980