
La Recherche. Numéro spécial sur les nombres Ndeg.278; Juillet/Aout 1995.
"La musique est la science du nombre rapportée aux sons". (Jean de Garlande, 1275) "L'action de l'ouye n'est autre chose que le desnombrement des battements de l'air, soit que l'âme les compte sans que nous l'apercevions, ou qu'elle sente le nombre qui la touche" (Mersenne, vers 1636). "La musique est un exercice occulte de l'arithmétique de l'âme qui ne sait pas qu'elle compte" (leibniz, 1712).
Comme le laissent entrendre ces citations, la musique et les nombres ont entretenu une relation profonde et constante pendant toute l'histoire la civilisation occidentale. Depuis les précurseurs grecs et latins jusqu'à la période moderne, où cette relation tend à se matérialiser à travers l'utilisation généralisée de l'ordinateur, un dialogue fécond et quelquefois tendu s'est tenu entre "harmonistes par calcul" convaincus de l'intérêt de la théorie et "harmonistes par l'oreille" défendant la supériorité de l'intuition. Le débat est ancien, puisque ces deux expressions désignaient au début du moyen âge deux écoles de pensée antagonistes dont le dialogue quelquefois conflictuel se continue aujourd'hui autour de la pratique de l'informatique musicale. Les analystes de la musique admettent cependant pour la plupart que chez tout compositeur ces deux fonctions, calcul et intuition, sont présentes dans des proportions variables.
Jusqu'au XVIIIème siècle la musique constitue sous l'angle de la science des nombres un champ de spéculation théorique et d'expérimentation pratique pour beaucoup savants, qu'ils soient eux même compositeurs ou non. De Pythagore ou Boèce à Kepler, Rameau ou Euler, il est peu d'entre eux qui n'aient commis un traité musical ou du moins qui n'aient associé à un moment ou à un autre dans leur oeuvre les concepts mathématiques, astronomiques, philosophiques à ceux de la musique.
Aristoxène au IVème siècle puis Pythagore au Vème siècle avant J.C., observant les propriétés acoustiques d'une corde vibrante dont la longueur est modifiée par un stylet mobile, pensèrent les premiers à caractériser les relations entre sons musicaux par des proportions de longueur de corde.
Au VIème siècle, Boèce, philosophe d'inspiration pythagoricienne et platonicienne, élabora un traité, De Institutione Musica, qui s'imposa par la suite comme la référence obligée des théoriciens de la musique durant tout le moyen âge. Dans cet ouvrage, Boèce envisage toutes les relations numériques connues et leur interprétation musicale : proportions de nombres entiers classifiées en familles diverses, suites numériques dont celle des nombres premiers, moyennes arithmétiques ou géométriques. Reprenant les principes du système de Pythagore, il les place dans une perspective nettement spéculative allant, par degrés successifs, des relations de base entre propriétés acoustiques et proportions numériques jusqu'à la musique des sphères, dispositif cosmogonique où s'articulent, en un tout cohérent réglé par l'ordre des nombres, les grands cycles de la nature, le mouvement des corps célestes, les éléments primordiaux, en une sorte de symphonie symbolique inaccessible à nos sens mais réglée par le même ordre.
La musique fait alors partie du Quadrivium, ensemble des quatre grandes disciplines de la pensée rationnelle. A ses cotés figurent arithmétique, géométrie et astronomie. Les savants qui s'adonnent à ces études ne sont pas spécialisés. Expériences et spéculations croisées issues de tous ces domaines s'échangent et se fertilisent mutuellement, souvent au sein d'un même ouvrage. Comme l'a traduit Boèce, un substrat philosophique commun justifie cette "pluridisciplinarité" : l'univers réglé par Dieu est harmonie et cette harmonie s'exprime dans les manifestations de la nature comme dans les créations de l'homme, dans la musique comme dans le ballet des astres et planètes. Arithmétique et géométrie constituent des modèles, au sens ou nous l'entendrions aujourd'hui, de cette harmonie des sphères. Comprendre le mystère caché des nombres, c'est alors comprendre le fonctionnement de l'univers, accéder au principe divin qui met la matière en mouvement, et, de manière tout à fait cohérente dans le contexte idéologique de l'époque, pénètrer les arcanes de la musique qui est une représentation sensible de cet ordre numérique.
Les auteurs de traités du XIIème au XIVéme siècle, Jean de Murs, Jean de Garlande, Franco de Cologne, Philippe de Vitry et bien d'autres, affrontent un problème musical et acoustique dont la solution ne sera trouvée de manière satisfaisante qu'au XXème siècle grâce à la théorie des bandes critiques : certains sons, lorsqu'on les entend simultanément produisent une impression agréable, d'autres un sentiment désagréable de tension, de frottement, de ruguosité dirait on aujourd'hui. Consonance et dissonance sont des concepts clés pour comprendre le fonctionnement musical ; en acquérir la maîtrise devient une question centrale au cours de la période évoquée car la polyphonie, superposition de plusieurs voix menant un discours musical "parallèle" et néanmoins cohérent, s'y développe considérablement, jusqu'à atteindre des sommets de richesse et de complexité lors de la période dite de l'Ars Nova (du titre d'un ouvrage de Philippe de Vitry) puis de l'Ars Subtilior ("art plus subtil", à la fin du XIVème). C'est à un travail de classification que se livrent les auteurs de traités, en utilisant un instrument appelé monocorde [voir figure] : consonance parfaite, moyenne, imparfaite, dissonance parfaite (la pire), moyenne, imparfaite -- acceptable à la rigueur comme consonance. Cette taxinomie est mouvante, les catégories sont mobiles car n'ayant pas de sens dans l'absolu, nous le savons mieux aujourd'hui. Tel rapport entre deux notes, consonant dans le registre aigu devient dissonant dans le grave. Telle dissonance classée comme telle par un auteur est considérée comme consonance par un autre. Ce travail de classification s'applique alors aux proportions numériques qui définissent la relation entre deux sons dans la tradition Pythagoricienne.

Au manque de moyens expérimentaux qui permettraient d'affiner le concept de consonance s'ajoute la difficulté inhérente à cette volonté toujours vive de tout faire cadrer avec l'harmonie universelle. Vouloir comprendre dans le même modèle la musique humaine et celle des sphères constitue certainement une difficulté majeure; heureusement, le discours radical et spéculatif du Musicus, du théoricien, est-il équilibré par la pragmatique du Cantor, l'éxécutant, le praticien. La pratique musicale a toujours été en avance sur la théorie, lui proposant, toujours renouvelé par telle création inattendue, un horizon qui s'échappe à mesure qu'elle croit l'atteindre.
La musique polyphonique peut être analysée selon les deux catégories de l'harmonie et du contrepoint. Selon le Dictionnaire encyclopédique de la musique de l'Université d'Oxford, "Si l'on définit le contrepoint comme le désaccord entre les voix ou les parties d'une oeuvre, l'harmonie peut être considérée comme l'élément d'accord entre ces parties". Par accord il faut entendre ici la consonance se produisant lorsque les voix se superposent à un instant donné.Le désaccord autorisé par le contrepoint est le degré de liberté qui permet aux différentes voix de s'émanciper et de trouver leur propre logique mélodique, tout en respectant la consonance harmonique aux points clés du parcours musical spécifiés par les règles. Du Xvème au XVIIème siècle fleurissent les traités de contrepoint tels ceux de Johannes Tinctoris ou Gioseffo Zarlino. Très schématiquement, on peut considérer le contrepoint comme un ensemble de décisions locales déterminées par des règles contextuelles : si, à un instant donné, les différentes notes superposées ont tel type de relations de consonance ou de dissonance, à l'instant suivant tel autre type sera autorisé ou interdit, les notes de chacune des voix évoluant entre les deux points selon des mouvements (parallèles, contraires, petits ou grands sauts etc.) eux aussi déterminés par les règles. Cette pensée par règles locales induit une conception de la partition qui ressemble à un immense arbre de possibilités, chaque choix déterminant les possibilités de choix futurs, et déplace progressivement les objectifs théoriques de l'analyse de la consonance per sui vers l'étude combinatoire. Voir Figure.

Ainsi, Mersenne, dans son Harmonie Universelle (1636), se demande s'il est possible de composer le meilleur chant imaginable ; il répond par la négative car le nombre de chants possibles est trop grand et l'on ne pourrait procéder par une technique d'essais et d'erreur. Il se donne néanmoins la peine d'effectuer des dénombrements fastidieux dont il ne donne que les résultats [voir figure dénombrement].

Le lecteur apprend ainsi qu'il existe 362880 mélodies de neuf sons sans répétition (362880 est la factorielle de 9) et seulement 90720 si ces neufs sons ont été choisis parmi sept dont le premier peut être répété 2 fois, le deuxième 2 fois, et les 5 derniers une fois seulement. Enfin, si ces sept sons peuvent eux même être choisis dans un réservoir plus grand de 22 notes (trois octaves) 324 906 785 280 mélodies sont obtenues. Dans son étude sur Mersenne le musicologue Edouard Knobloch a vérifié ces calculs et leur a associé les formules de combinatoire qui sont aujourd'hui usuelles. Il note cependant que ces formules assez compliquées et faisant intervenir factorielles, arrangements et combinaisons n'ont été explicitées par le mathématicien Bernoulli que cinquante ans après la parution de l'Harmonie Universelle. Si la litanie de ces grands nombres a finalement assez peu servi les compositeurs, sinon à leur faire sentir le caractère miraculeux du choix qu'opère avec une certaine sûreté le créateur parmi le foisonnement du possible, l'intérêt du texte de Mersenne vient de ce qu'il marque une évolution parallèle de la théorie musicale, qui s'intéresse de plus en plus, au delà du phénomène artificiellement isolé de la consonance, à l'articulation du discours musical dans toutes ses dimensions, et d'une conception philosophique de l'univers, d'abord envisagé comme horlogerie immuable, à la vision inaugurée par Leibniz d'un monde résultant, tel un langage, de l'engendrement combinatoire des possibles.
Cette systématisation de l'idée combinatoire aux XVIIème et XVIIIème siècles a débouché naturellement sur l'idée d'automatiser certains aspects de la production musicale et sur l'apparition des premières "machines à composer", précurseurs de nos ordinateurs. La "caisse musicale" (arca musurgica) d'Athanasiuss Kircher contient des lattes mobiles, sur lesquelles sont portées des nombres codant divers paramètres musicaux, et qui peuvent être déplacées ou permutées. A la fin du XVIIIème siècle apparaissent des jeux musicaux comme le Musikalisches Wurfespiel de Mozart qui, à base de tables, de cartes et de dés, engendre par un principe de simple combinatoire des menuets de 16 mesures. Le componium de Diederich Winkel (1826) est un "improvisateur mécanique" basé sur des mécanismes d'horlogerie et qui a l'avantage de posséder une sortie sonore directe utilisant des tuyaux d'orgues.

L'apparition de l'ordinateur dans la deuxième moitié du XXème siècle suscite un regain d'intérêt pour les questions combinatoires : les espaces de recherche gigantesques entrevus par Mersenne sont, semble-t-il à portée de puissance des calculateurs. Le début des années 60 voit fleurir un certain nombre d'expériences : Xenakis, Hiller, Barbaud sont alors les pionners de la composition assistée par ordinateur. Mais, d'une part, même avec des puissances de calcul non négligeables, la combinatoire musicale à l'échelle d'une pièce entière et non plus de quelques accords reste d'un coût considérable. D'autre part, un problème qui avait été quelque peu escamoté tant que ces questions n'avaient pas rejoint le champ expérimental resurgit : l'énumération de solutions n'est rien si l'on ne dispose pas d'un modèle fixant les critères de choix. Et l'on ne sait toujours pas pourquoi devant la multitude des solutions le compositeur, sûr de son métier, va directement à la bonne -- une chose est certaine cependant : le praticien ne procède pas de manière énumérative.
Xenakis, considéré par beaucoup comme un des grands compositeurs du siècle, n'en est pas resté à l'utilisation de l'ordinateur comme système de production combinatoire. A partir d'une réflexion sur l'hisoire de la musique et de ses relation avec les sciences il a inauguré une approche dans laquelle le phénomène sonore est envisagé sous un angle statistique et peut être modélisé selon des lois stochastiques. Il établit néanmoins un pont avec une tradition séculaire dans l'utilisation qu'il fait de l'arithmétique des nombres entiers, des proportions liées au nombre d'or [voir encadré sur le nombre d'or], et dans les relations qu'il établit entre ses réalisations musicales et architecturales.
L'utilisation de l'ordinateur dans la composition progesse de manière significative depuis quelques années. Sans chercher à confier à la machine l'organisation à tous les niveaux d'une architecture musicale, ce qui reste hors de portée, les musiciens construisent avec son aide des matériaux structurés qui peuvent consister en systèmes d'échelles, d'accords, de rythmes, de timbres sonores. Ces systèmes, ou modèles, une fois programmés donnent lieu par paramétrage à une exploration systématique. Les programmes d'analyse acoustique, utilisant notamment la transformée de Fourier, permettent enfin de chercher de nouveaux éléments au coeur même des sons et d'élargir le champ d'investigation à l'ensemble de l'univers sonore, notamment aux sons inharmoniques dont les composantes spectrales peuvent être dans des rapports irrationnels. Contrairement à l'opinion quelque fois exprimée qui voudrait voir dans l'utilisation de l'ordinateur en musique une soumission aliénante à la modernité technologique, nous n'avons peut être jamais été aussi proche de l'esprit de recherche et d'innovation qui prévalait au moyen âge. Il suffit d'ouvrir les traités anciens, emplis de graphes, de schémas fonctionnels, de caculs numériques, d'algorithmes, pour se convaince que ces ancètres eussent adoré avoir un ordinateur à portée de main pour faciliter leurs calculs et expérimenter de nouvelles idées.
Les notes de la gamme diatonique (do, ré, mi, fa, sol, la, si, do) se différencient par leur hauteur qui peut être caractérisée de manière univoque par la fréquence de vibration de l'onde sonore associée. La relation existant entre deux notes est appellée intervalle par les musiciens. Ainsi, l'intervalle entre do et sol est qualifié de quinte juste et celui allant de do à do sept notes plus haut est une octave. Ces intervalles sont très stables mais les rapports de fréquence précis qui les caractérisent ont varié au cours de l'histoire suivant l'évolution des théories de la consonance. Le phénomène physique qui sous-tend l'existence des intervalles musicaux est la présence, dans le spectre de fréquences d'un son périodique, d'énergie aux fréquences multiples (harmoniques) de la fréquence fondamentale. Ces "hauteurs" cachées sont audibles sous certaines conditions, et les proportions formées entre les premières harmoniques de la série sont caractéristiques des intervalles les plus consonants : unisson (1:1), octave (2:1), quinte (3:2), quarte (intervalle de do à fa, 4:3).
Pythagore et ses disciples, au Vème siècle A.C., déterminèrent des proportions, non de fréquence mais de longueur de corde vibrante, ce qui est équivalent à une inversion près. Leur approche expérimentale était soumise à des contraintes d'un ordre mystique qui les poussait à exprimer toutes les relations sous la forme de proportions de nombres entiers puissances des chiffres 2 et 3, considérés comme des générateurs universels. Exprimée selon ce formalisme, la gamme diatonique contient les rapports de fréquence suivants, donnés pour chaque note relativement au do d'origine.
1 9/8 81/64 4/3 3/2 27/16 243/128 2
do ré mi fa sol la si do
Bien que cette contrainte symbolique ait éloigné les pythagoriciens d'une formulation plus proche de la réalité physique, l'influence de ces derniers se fera sentir durant tout le moyen âge. Reprenant la classification des consonances données par Francon de Cologne vers 1280, le musicologue Christian Meyer en a retrouvé la source pythagoricienne dans le commentaire de Calcidius sur le Timée de Platon, sous la forme d'un diagramme à deux branches portant les puissances de 2 et de 3, dans lequel les lignes transversales dénotent des proportions. Les lignes horizontales délimitent les catégories encore en usage au XIIIème siècle : consonances (concordantiae) et dissonances (discordantiae) parfaites, médianes et imparfaites.
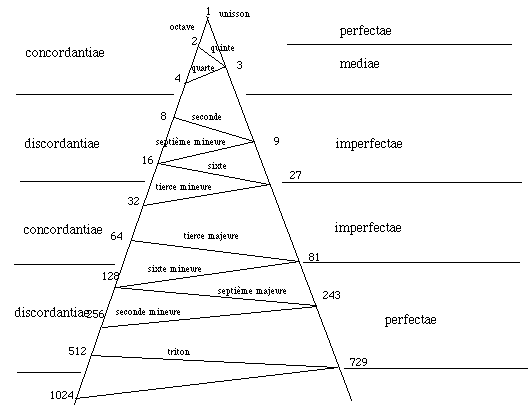
[d'après Meyer 1992]
Il reviendra à Zarlino (1573) de caractériser la gamme diatonique selon des proportions directement dérivées de la série harmonique :
ratios : 1 9/8 5/4 4/3 3/2 5/3 15/8 2
gamme diatonique do ré mi fa sol la si do
On s'aperçoit que les consonances (indiquées en gras) correspondent aux ratios les plus simples, c'est à dire à ceux qui sont formés le plus tôt dans la série harmonique, ce qui s'explique par le fait que les premières hamoniques sont les plus fortes en énergie, et doit être mis en relation avec l'intuition pythagoricienne que les proportions de petits nombres entiers étaient la clé de l'harmonie cachée.
En 1877, Hermann Helmholz, fonde la consonance sur la structure harmonique interne des deux sons formant un intervalle musical : lorsque les fondamentales des deux sons sont dans un rapport simple, par exemple 3:2, certaines parmi les premières harmoniques de la série entrent en coïncidence, ici la 2ème et la 3ème, créant un sentiment de fusion agréable. Lorsque ce n'est pas le cas, certaines harmoniques, proches sans être égales provoquent des battements (la "ruguosité") qui perturbent l'audition et sont identifiés comme dissonances.
Dans la figure suivante, helmoltz a construit à la main et à l'oreille une courbe de dissonance obtenue en superposant deux Do (C') joués par des violons et en faisant glisser continument le second jusqu'au do (C'') de l'octave supérieure. Les battements sont comptés pour chaque paire d'harmonique et reportés sur la courbe. Les consonances sont les minima de la courbe (c : unisson, g' : quinte, c'' : octave supérieure). On voit par exemple que l'intervalle de quinte do (c') à sol (g') est une consonance parfaite, mais que dans la région à gauche et à droite de g' la dissonance augmente rapidement car les harmoniques 2 de sol et 3 de do (indiquées 2:3), qui coïncidaient, se désaccordent, provoquant desbattements, de même pour les paires 4:6 et 6:9.

En 1965, R. Plomp et W. Levelt de l'Institut pour la perception d'Eindhoven précisent la notion de ruguosité en partant la théorie des bandes critiques formulée par E. Zwicker (Université technique de Munich) en 1957: selon ces auteurs, il existe autour de chaque fréquence du continuum spectral une bande critique de fréquence dont la largeur est quasi proportionnelle à sa fréquence centrale. Lorsque deux sons sont entendus simultanément, le phénomène de ruguosité se produit à chaque fois qu'une harmonique de l'un entre dans la bande critique d'une harmonique de l'autre. En effet, c'est dans ce cas un même groupe de cellules nerveuses qui seront excitées dans l'oreille interne, perturbant ainsi la discrimination entre les deux harmoniques. La figure suivante, calculée à partir d'un modèle informatisé des bandes critiques, représente la courbe de consonance obtenue à partir de deux sons contenant six harmoniques, le premier à 250 Hz, le second variant entre 250Hz et 500Hz. Ce sont ici les maxima de la courbe qui indiquent les consonances (les rapports 1:1, 3:2 et 2:1 représentent les intervalles d'unisson, de quinte et d'octave entre les fondamentales des deux sons. ) .
 Encadré
: le nombre d'or en musique.
Encadré
: le nombre d'or en musique.
Le nombre d'or correspond, d'un point de vue géométrique, à une proportion partageant un segment en deux parties inégales dont la plus grande est dans le même rapport au tout que la plus petite à la plus grande. Il s'exprime également comme la limite du rapport entre deux nombre successif de la série de Fibonacci. Représentant un principe de croissance equilibré, les grecs en firent un usage remarqué dans leur système esthétique. Dès le troisième siècle avant Jésus Christ, Euclide laisse un témoignage des propriétés de ce nombre dans ses éléments de géométrie. Avec l'émergence de la pensée pythagoricienne qui allait marquer tout le Moyen-Age, des qualités mystiques furent associées à ce nombre, les relations numériques exprimant l'équilibre et l'harmonie de l'univers et rendant compte de la création divine.
Dans le domaine musical, le nombre d'or a été utilisé jusqu'à notre époque par de nombreux compositeurs. Dufay, au XVème siècle, y eut recours pour certaines de ces oeuvres. Des compositeurs de la Renaissance comme Roland de Lassus l'utilisèrent comme moyen de structurer leur discours musical en relation avec l'aspect réthorique de celui-ci. Il semble que l'on puisse retrouver ce principe formel dans certaines symphonies de Mozart et de Haynd et dans des sonates de Beethoven.
A l'aube de notre siècle, le nombre d'or fut également utilisé par des compositeurs comme Debussy, Bartok, Ravel ou encore Webern.
Roy Howat a rappelé comment Debussy, esprit curieux s'intéressant à la numérologie et aux structures numériques dans l'art a eu connaissance d'articles sur les proportions et sur le nombre d'or publiés dans des revues symbolistes, mouvement artistique et intellectuel auquel Debussy fut associé. On peut en déduire, comme l'a montré Roy Howatt, que Debussy utilisa, sans doute, de manière consciente ces techniques dans certaines de ses oeuvres comme Reflets dans l'eau ou la Mer.
Le musicologue hongrois Ernö Lendvai a mis en évidence comment Bartok en fit un principes de structuration dans un grand nombre de ses oeuvres. Le premier mouvement de la musique pour cordes percussions et celesta est construit sur ce principe. Ce mouvement comprend 89 mesures. La mesure 56 correspondant à la section d'or marque le point culminant d'une progression amorcée dès le début de l'oeuvre, se traduisant par une écriture de plus en plus dense et dramatique, et le point de départ d'un processus inverse à celui constaté jusqu'alors. La densité d'écriture va peu à peu diminuer pour revenir à une seule ligne mélodique puis au silence. A l'intérieur de ces deux sections principales la proportion de chacune des sous-sections est également conçu d'après le nombre d'or. D'autres oeuvres utilisent ce principe de structuration qu'il s'agisse du divertimento pour orchestre à cordes, de la sonate pour deux pianos , des contrastes pour piano, violon et clarinette ou de l'allegro barbaro. On pourrait ainsi multiplier les exemples.
Plus proche de nous, Stockhausen a utilisé le nombre d'or dans certaines de ses oeuvres. Le Klavierstucke IX est basé sur ce nombre remarquable. La durée des sections est déterminée par la série de Fibonacci. La disposition des accents, les mouvements dynamiques dans les sections reposant sur des accords répétés, les rapports existants entre ces sections et d'autres sections sont calculés d'après la "divine proportion". Comme pour Bartok, l'utilisation du nombre d'or est liée, dans cette oeuvre, à un souci de créer un principe d'organicité .
Xenakis a eu également recours dans certaines de ses oeuvres à ce principe proportionnel. Metastasis, datant de1953-54 est intéressante à cet égard car elle intègre des processus compositionnels basées sur la série de Fibonacci et sur les principes du modulor de Le Corbusier utilisés comme système de mesures et élément unificateur. Jouant constamment sur la notion d'espace (l'oeuvre est pensée pour soixante et une parties séparées), faite d'évolution de volumes et de transformation de surfaces sonores, l'oeuvre préfigure musicalement ce que sera la réalisation du pavillon Philips conçu par Xenakis pour l'exposition universelle de Bruxelles en 1958. Dans son livre "musique formelle" Xenakis évoque "la chaîne causale d'idées qui [le] conduisit à formuler l'architecture du pavillon Philips à partir de la partition de Metastasis". [figure : partition de Metastasis et Pavillon Philips].
Références Bibliographiques
Ouvrages anciens
Boèce. De Institutione Musica. V-VIème siècle.
Jean de Murs; Musica Speculativa. 1233.
Jean de Garlande. De mensurabili Musica. 1275.
Kepler. WeltHarmonik. 1619.
Zarlino (Gioseffo) Le Institutioni harmoniche 1558.
Mersenne. Harmonie Universelle. 1636.
Galilée. Discours sur les deux principaux systèmes du monde. 1636.
Kircher. Musurgia Universalis. 1650.
Leibniz. Dissertation sur l'art combinatoire. 1666. (?? vérifier).
Bernoulli. Ars Conjectandi. 1713.
Rameau. Traité de l'harmonie réduite à ses principes naturels. 1722.
D'Alembert. Eléments de musique théorique et pratique suivant les principes de Mr. Rameau. 1762. ou 1779.
Leonhard Euler. Essai d'une nouvelle théorie de la musique. 1739, trad. française 1839.
Ouvrages récents.
HelmHolz H. On the sensation of Tone. (1877). Dover, New York, 1954.
Zwicker, Flottorp, Stevens. Critical Bandwith in Loudness Sommation. J.ofAc.Soc.of.Am. 29 (1957) : 48.
Plomp, R., Levelt, W. Tonal Consonance and Critical Bandwidth. J.Acoust.Soc.Amer.38, 548-560. 1965.
Gut S. La notion de consonance chez les théoriciens du moyen âge. Acta Musica. Vol XLVIII. 1976.
Xenakis (Iannis) Musiques formelles. Nouveaux principes formels de composition musicale. Paris : Stock, 1981.
Pierce J. Le son musical. Bibliothèque Pour la Science, Belin. 1983.
Christian Meyer. Mathématique et musique au moyen âge. Quadrivium : Musiques et sciences. La Villette, Paris. IPMC, 1992. (Acte du colloque organise du 8 au 10 mars 1991 a Metz par l'IPMC)
Eberhardt Knobloch. Rapports historiques entre musique, mathématique et cosmologie. Quadrivium : Musiques et sciences. La Villette, Paris. IPMC, 1992. (Acte du colloque organise du 8 au 10 mars 1991 a Metz par l'IPMC)
Roy Howatt. Debussy in proportion. A musical analysis. Cambridge University Press.1983.
Jean Bernard Condat Editeur. Nombre d'or et musique. Peter Lang, 1988.