Gérard Assayag, Carlos Agon, Joshua Fineberg, Peter Hanappe

Ircam 1 Place Stravinsky 75004 Paris.

e-mail : assayag@ircam.fr

" Longtemps je me suis couché sur le papier réglé "

Claudy Malherbe

1. La note en abyme

L'équipe représentations musicales de l'Ircam conçoit et développe des systèmes informatisés d'aide à la composition musicale. Parmi toutes les significations que l'on peut associer à cette expression, nous nous restreignons à ce que l'on nommera l'aide à l'écriture. Cela signifie que notre problème n'est pas la performance en temps réel, non plus que l'analyse ou la synthèse des sons, bien que ces divers aspects puissent être traités comme extensions nécessaires à l'expérimentation. La substance que traiteront nos modèles, c'est l'écriture elle même, prise comme univers de formes, de structures, de relations.

Une fois cet objectif posé, la question de la notation surgit immédiatement. En effet, qui dit écriture dit notation. Risquons une définition : la notation est un dispositif a deux faces : une face concrète et sensible, un jeu de signes matérialisables (sur la feuille, sur l'écran) et une face abstraite, un jeu de relations contraignant l'utilisation de ces signes. L'écriture est le processus dynamique d'utilisation de la notation pour mettre en forme des structures et des relations de plus haut niveau. Le premier de ces niveaux supérieurs de structuration est directement discernable dans la substance concrète de la notation : par exemple une répétition. Par analogie avec le langage on qualifiera ce niveau de syntaxique. Le second de niveau de structuration de l'écriture n'est pas directement discernable : il faut pour cela imaginer une exécution virtuelle, ce que font les musiciens expérimentés à la lecture d'une partition. Par exemple, l'évolution d'une couleur harmonique. Il y a besoin ici d'un au-delà de la notation qui puise dans notre expérience et notre imaginaire et c'est pour cela, toujours par analogie, qu'on proposera de qualifier ce niveau de sémantique.

Nous avons évoqué le cas de figure, traditionnel, de la partition musicale. Mais dans le cas qui nous préoccupe, c'est à dire avec l'ordinateur, la partition n'est plus qu'un aspect parmi d'autres. En effet, le compositeur devant son écran manipule divers objets dont certains sont des objets de calcul. Cela n'est pas en soi nouveau : bien naïf qui croit que la musique s'écrit directement sur la portée. Mais avec l'ordinateur, le degré d'interaction est tel, entre objets calculés, fragments littéraux de musique injectés dans le système, éléments de matériaux de bas niveau, structures formelles de haut niveau que c'est la notion même de partition qui tend à s'effacer devant l'idée de modèle dynamique (et informatisé) de partition.

C'est alors à tous ces niveaux qu'intervient la notation. Notation des programmes calculant des matériaux musicaux. Notation des résultats de ces programmes, sous forme mathématique (des courbes) ou musicale (des notes). Notation des structures formelles qui articulent ces matériaux. Notation des programmes qui prennent en entrée ces structures formelles et les transforment encore. On entre dans une récursion infinie qu'il appartient au créateur de terminer quand il le décide en calibrant le niveau de complexité qu'il désire (ou qu'il peut) maîtriser.

Notre équipe s'est spécialisée dans les langages de programmation visuelle pour le musicien. La considération du programme comme une notation devient dans ce cas encore plus évidente, le programme s'inscrivant alors dans une schématique. Nous avons essayé de rendre plus continue encore la transition entre les divers niveaux de schématique intervenant dans la conception musicale. Ces réflexions se concentrent dans un environnement qui s'appelle -- provisoirement -- OpenMusic.

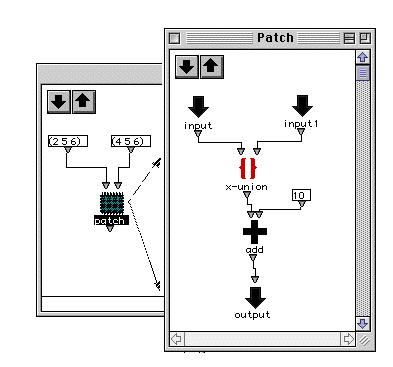
OpenMusic prend la suite, dans notre travail, de PatchWork, un environnement qui utilisait déjà la notion de programmation visuelle. De même que dans PatchWork, l'unité de calcul est la fonction. Une fonction est matérialisée par une icône qui dispose d'entrées et de sorties. Les icônes se connectent entre eux pour former un patch. Le patch est l'unité de programme. Il peut à son tour être condensé en un icône et, masquant sa complexité interne devenir à son tour un atome de calcul dans un autre patch. Premier aspect récursif dont on jouera pour montrer ou cacher la complexité. La programmation devient alors un art graphique par lequel on essaiera de rendre évidents les aspects syntaxiques et sémantiques.

A la différence de PatchWork, les fonctions sont dotées de généricité (ou polymorphisme). Une fonction est alors à considérer comme un ensemble de méthodes, qui implémentent chacune un calcul dépendant du type de ses arguments. Ainsi, la fonction "addition" appliquée à deux nombres en fera la somme, et appliquée à deux structures musicales pourra en faire la fusion rythmique, si c'est là la signification que l'on désire lui donner. Cela représente un avantage considérable qui est de favoriser l'abstraction. Le même icône sera utilisé dans les deux cas, et dans les deux cas un aperçu rapide du programme donnera une indication du type d'opération en jeux. On passe donc de la notion de calcul à la notion de classe de calcul par un artifice de notation : l'identité visuelle.

En plus des fonctions est utilisée la notion d'objet. Un objet est une instance, une concrétisation, d'un autre objet, que l'on appelle une classe, et qui est un modèle abstrait nécessaire à sa fabrication. Par exemple, les classes entier, tableau, structure-musicale, etc. Une classe peut avoir des sous-classes, par exemple les classes séquence-midi ou partition sont des sous-classes de structure-musicale. Les objets créés directement par l'utilisateur ou résultats d'un calcul peuvent être matérialisés : ils émergent littéralement à la surface du patch, sous formes de nouveaux icônes, et deviennent des sources de valeur ou des lieux de stockage d'information. Un objet peut être un simple nombre, un texte ou une polyphonie à vingt-quatre voix. Les objets peuvent être mis dans d'autres objets, etc.

Les objets comme les patches peuvent être "plongés" dans une maquette, qui est une sorte de surface dont une dimension est le temps. Ainsi sont créées, par superposition et concaténation, les articulations entre objets élémentaires. Une maquette peut être plongée dans une maquette et articulée dans le temps à d'autres objets ou d'autres maquettes. Ainsi, par récursion, seront emboîtés les niveaux successifs de l'articulation formelle. Une maquette peut être plongée dans un patch, et devenir à son tour un atome de calcul : la structure musicale qu'elle représente devient source de valeur, simple paramètre pour un calcul de plus haut niveau. Encore une fois il appartient au créateur de calibrer la complexité, mais le système lui même n'impose aucune limite.

Il est clair qu'une maquette est une notation. Le patch aussi, d'une autre sorte. Mais les uns sont plongés dans les autres et réciproquement : à ce stade, ce qu'apporte l'ordinateur n'est plus seulement quantitatif mais qualitatif. On bascule dans la mise en abyme de la notation.

Un patch plongé dans un autre patch.

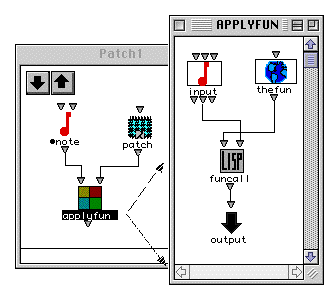
Un patch passé en argument fonctionnel à un autre patch. Ce type d'opération d'ordre 2 permet de rendre paramétrisable la nature même d'un calcul .

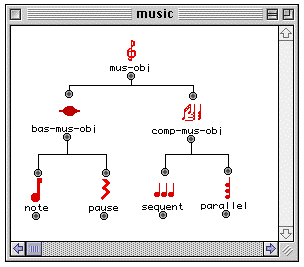
Une hiérarchie de classes

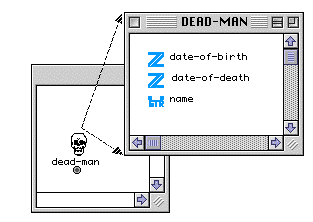
Les champs (typés) d'une classe

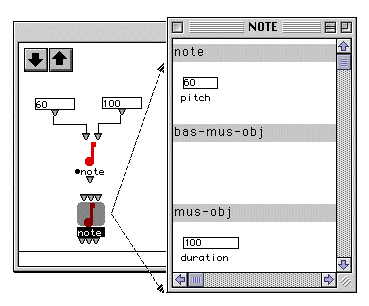
La classe note permet de générer des instances concrètes de notes. Un mode d'évaluation graphique permet de faire "émerger" l'instance dans la fenêtre (objet en bas de la fenêtre).

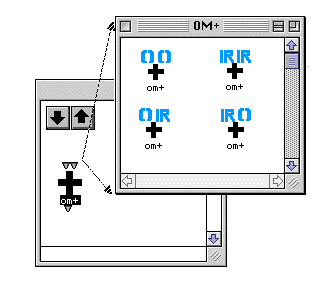
La fonction générique d'addition et quelques méthodes pour les nombres (type R) et les listes (type ()).

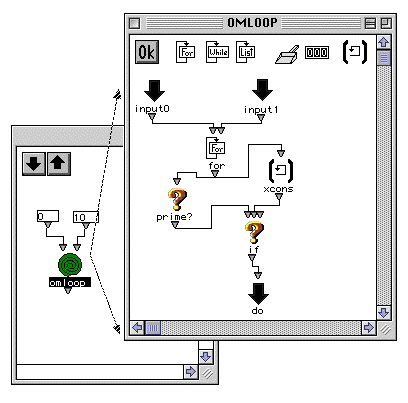
Un itérateur complexe. Le calcul montré dans cet exemple est l'extraction de la liste des nombres premiers entre deux bornes (0 et 10).

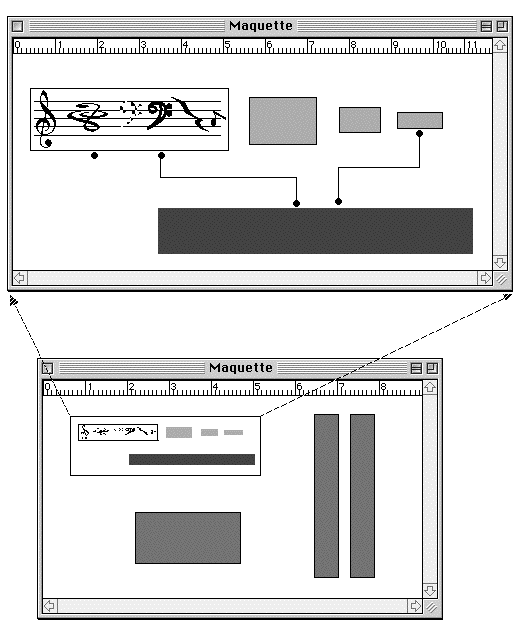
Une maquette (en bas) contenant une autre maquette et trois patches. Les connections dans la maquette contenue (ouverte en haut) permettent de créer des échanges de données entre les divers patches qui la composent.

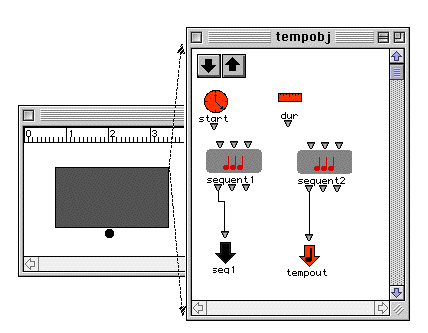
Lorsqu'un patch est plongé dans une maquette, il obtient deux entrées supplémentaires qui sont sa position temporelle et sa durée. La sortie tempout est la sortie correspondant à la structure musicale pertinente du point de vue de la maquette. La sortie seq1 est une sortie arbitraire rajoutée par l'utilisateur et qui permet de faire communiquer le patch avec d'autres patches dans la maquette.

Ainsi, seule sequent2 appartient à la "surface musicale", c'est à dire à ce qui serait effectivement joué et imprimé dans la partition finale. Sequent1 appartient à "l' inconscient" de la partition, c'est à dire un matériau intermédiaire, associé à la région de la partition figurée en grisé dans la maquette, et qui peut éventuellement alimenter en données d'autres régions à travers un lien..

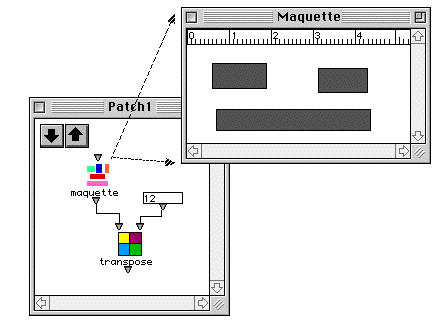
Une maquette a été plongée dans un patch. On lui applique un opérateur de transposition.

Un WorkSpace (espace de travail) permet de ranger tous les objets.

2. Le temps abymé

Les maquettes ouvrent un espace récursif (une mise en abyme) dans lequel s'articulent en largeur, en hauteur et en profondeur des structures musicales qui peuvent être : des séquences Midi, des fichiers audio, des scripts de synthèse, des structures musicales notables sous la forme de partitions, ou des patches qui calculent les précédents. Ces patches peuvent contenir à leur tour des maquettes et les maquettes peuvent à leur tour figurer dans un patch comme source de valeur.

Du point de vue temporel, on est amené à faire coexister des entités qui ressortent de systèmes d'unités très différent. Système d'unités plat en millisecondes (par exemple) pour les fichiers sons et les séquences Midi. Système d'unités hiérarchiques fonctionnant sur le principe du partage d'entiers pour les structures musicales symboliques. On comprendra aisément ce dernier point à partir d'un exemple. Le fragment rythmique suivant :

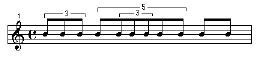
peut être schématisé selon le partage d'entiers suivant, dans lequel la noire vaut 1 (u = 1):

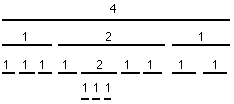
sans qu'il soit besoin de commenter beaucoup plus. Si l'on note la structure récursivement :

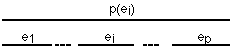
on peut noter l'extension (durée) du composants ei par la formule

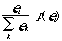
Ainsi, la croche de triolet la plus emboîtée de notre exemple a pour extension :

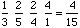
Nous faisons le choix de n'utiliser que des nombres entiers pour représenter les structures temporelles emboîtées. Nous espérons, par un choix judicieux d'échelles, faciliter le passage à la notation ainsi que la coexistence d'objets décrits en temps hiérarchique et en temps continu. Nous voulons aussi éviter les problèmes de conversion entre entiers et réels qui débouchent, dans le cas du rythme, à une non-inversibilité du processus de traduction entre temps hiérarchique et en temps continu.

Il suffit dans le dernier exemple de décider que la noire vaut 15 unités (u = 15), auquel cas l'extension de notre croche sera 4. Mais alors elle ne sera pas commensurable avec la croche du quatrième temps qui implique u = 2. Si l'on veut rendre commensurable toutes les valeurs, il faut choisir pour l'ensemble de la mesure u = ppcm(2,3,5) = 30. Dans ce cas, les valeurs recherchées seront 8 pour la croche de triolet et 15 pour la croche du quatrième temps.

Il sera ainsi toujours possible de calculer une valeur pour u, a un certain niveau de structure, qui rende commensurable toutes les valeurs contenues dans les niveaux immédiatement inférieurs. On peut calculer la valeur de u correspondant à l'ensemble d'une partition et en déduire toutes les valeurs des structures inférieures : voix, mesures, groupes, notes. Mais on arrive très vite à de très grands nombres, gérables dans certains environnement (e.g. BigNums en CommonLisp) mais qui posent tout de même des problèmes de mémoire et d'efficacité. De surcroît cette complexité n'est pas nécessaire à tous les niveaux : si l'on extrait une sous-structure (e.g. une mesure) d'une sur-structure (e.g. une voix) pour lui appliquer un opérateur (e.g. la jouer), une valeur de u locale, nécessaire et suffisante compte tenu de la complexité interne de la sous-structure, doit faire l'affaire. D'où l'idée d'un système d'échelles variables, toujours en nombres entiers, adapté à chaque niveau d'emboîtement des structures musicales.

Cette organisation est schématisée dans la figure suivante.

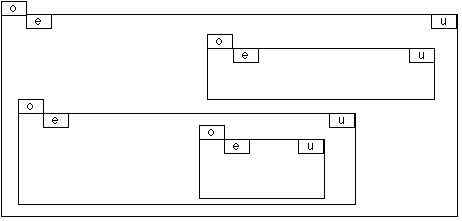
Toute structure musicale est un conteneur qui contient d'autres structures musicales. Tout conteneur a une extension temporelle (e) et un temps de début ou offset (o) relatif à son contenant. o et e sont des entiers qui s'expriment dans une échelle dont l'unité est une fraction 1/u de la noire, où u est un entier redéfinissable à chaque niveau d'emboîtement.

Ainsi les les offsets successifs des 6 notes suivantes par rapport au début du quintolet sont : 0, 6, 10, 14, 18, 24 pour u = 15.

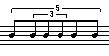
Chaque conteneur possède donc trois attributs entiers:

u qui définit l'échelle pour ce conteneur.

o est l'offset de ce conteneur, exprimé par rapport à l'attribut u du conteneur immédiatement englobant. o est égal à 0 s'il n'y a pas de conteneur englobant.

e est l'extension de ce conteneur exprimée par rapport à l'attribut u appartenant à ce même conteneur.

Les primitives de manipulation de base des structures musicales sont alors les suivantes :

NewContainer

Crée un container vide. u = 1 par défaut.

AddTo container1 container2 at

Place le container2 dans le container1 à la position at. at est exprimé en fraction de noire.

u = u(container1)

p = ppcm(u, denominator(at))

u(container1)= p

o(container2) = at * p

o(conti) = o(conti) * p / u pour tout conti sous-conteneur immédiat de container1

Insérer container2 dans container1.

RemoveFrom container1 container2

o(container2) = 0

Libère le container2 du container1.

QReduce container [n]

Calcule u' = ppcm ( u(conti) ) où conti parcourt tous l'arbre des containers dont container est la racine. Effectue ensuite u(conti) = u' puis change corrélativement les o(conti) et les e(conti). Rend donc toutes les parties de container commensurables.

Si n est spécifié, u' = ppcm ( u(conti), n)

QNormalize container

Fonction symétrique de Qreduce.

Affecte à chaque conti de l'arbre un u nécessaire et suffisant grâce à un calcul de pgcd sur les parties immédiates de conti.Change corrélativement les o(conti) et les e(conti).

Ainsi, pour ramener à la même échelle deux structures c et c' aux fins de les comparer, de les fusionner, etc., la séquence des opérations est la suivante :

c'' = NewContainer ()

AddTo (c'', c, 0)

AddTo(c'', c', 0)

QReduce (c'')

RemoveFrom(c'', c)

RemoveFrom(c', c')

Le modèle présenté ici s'applique naturellement aux structures musicales symboliques dans lesquelles les catégories traditionnelles de polyphonie, voix, mesures, groupes, sous-groupes, valeurs (container terminaux) sont aisément représentées comme des sous-classes de la classe container.

Mais il nous sert aussi à faire le lien, au sein des maquettes, entre ces structures symboliques et des objets hétérogènes comme les séquences audio ou Midi, et les scripts de synthèse.

Par exemple, si l'on voulait placer dans le même conteneur une séquence audio, au temps 1.3 secondes, et une structure symbolique au temps 4 secondes (avec une noire par défaut à 60) :

c = NewContainer ()

AddTo (c, csymb, 4)

AddTo(c, caudio, 1300/1000)

La lecture des valeurs après installation donnerait :

u(c) = 10, o(csymb) = 40, o(caudio) = 13

Si l'on voulait en extraire une partition mixte avec une impulsion de noire à 60, il serait facile de calculer que la séquence audio commence sur une seconde croche de triolet du deuxième temps et la séquence symbolique sur le quatrième temps.

L'évaluation et l'affichage d'un conteneur englobant des objets hétérogènes pourrait ressembler à l'image suivante :

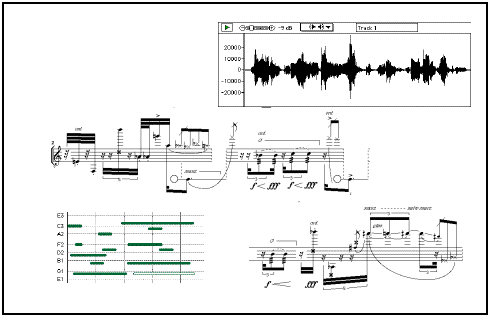
Ainsi, après avoir évoqué la mise en abyme des structures formelles de programmation et des objets musicaux, c'est à la mise en abyme du temps musical lui même que nous avons procédé. Ces structures récursives sont bien sûr présentes dans les représentations musicales traditionnelles ; l'informatique et particulièrement la composition assistée par ordinateur ouvrent à notre sens une opportunité inédite d'aller au bout de leur logique interne.

Remerciements

Les fragments de partitions utilisés dans la dernière illustration sont extraits de " Huskless " de Paul Steenhuisen.

Bibliographie

[Assayag 95] Assayag G., "Visual Programming in Music." Proceedings of the ICMC 96, Banff, 1996.

[Assayag & al 93] Assayag G., Rueda C. "The Music Representation Project at IRCAM." Proceedings of the ICMC 93, Tokyo, 1993.

[Laurson & al 90] Laurson, M. Duthen, J. "A compositional environment based on Preform II, PatchWork and Esquisse." Proceedings of the ICMC 1990. Glasgow 1990.

[Lindemann 90] Lindemann, E. "Animal: A Rapid Prototyping Environment For Computer Music Systems". Proceedings of the ICMC 1990. Glasgow. 1990.