Guessing the Composer's Mind: Applying Universal Prediction to Musical Style

Gérard Assayag (Ircam) , Shlomo Dubnov (Ben Gurion Univ.), Olivier Delerue (Ircam)

http://www.ircam.fr/equipes/repmus

Abstract

In this paper, we present a dictionary based universal prediction algorithm that provides a very general and flexible approach to machine learning in the domain of musical style. Such operations as improvisation or assistance to composition can be realized on the resulting representations.

1. Introduction

It is commonly admitted that musical perception is guided by expectations based on the recent past context. Predictive theories are often related to stochastic models which estimate the probability for musical elements to appear in a given musical context, such as Markov chains, already used extensively in computer music. The main problem with these models is that the length of musical context (size of memory) is highly variable, ranging from short figurations to longer motifs. Taking a large fixed context makes the parameters difficult to estimate and the computational cost grows exponentially with the size of the context.

2. Dictionary-based prediction

In our work we present a dictionary-based prediction method, which parses an existing musical text into a lexicon of phrases/patterns, called motifs, and provides an inference method for choosing the next musical object following a current past context. The parsing scheme must satisfy two conflicting constraints. On the one hand, one wants to maximally increase the dictionary to achieve better prediction, but on the other hand, enough evidence must be gathered before introducing a new phrase, so that a reliable estimate of the conditional probability is obtained. The secret of dictionary-based prediction (and compression) methods is that they cleverly sample the data so that most of the information is reliably represented by few selected phrases. This could be contrasted to better known Markov models that build large probability tables for the next symbol at every context entry. Although it might seem that the two methods operate in a different manner, it is helpful to understand that basically they employ similar statistical principles.

Incremental Parsing

We chose to use an incremental parsing (IP) algorithm suggested by Lempel and Ziv [LZ78]. IP builds a dictionary of distinct motifs by sequentially adding every new phrase that differs by a single next character from the longest match that already exists in the dictionary. For instance, given a text {ababa...}, IP parses it into {a,b,ab,aa, ...} where motifs are separated by commas. The dictionary may be represented as a tree (see last section).

Probability Assignment

Assigning conditional probability of a symbol given as context is done according to the code lengths of the Lempel Ziv compression scheme. Let c(n) be the number of motifs in the parsing of an input n-sequence. Then, log(c(n)) bits are needed to describe each prefix (a motif without its last character), and 1 bit to describe the last character (in case of a binary alphabet). For example, the code for the above sequence is (00,a),(00,b),(01,b),(01,a) where the first entry of each pair gives the index of the prefix and the second entry gives the next character. Ziv and Lempel have shown that the average code length c(n)log(c(n))/n converges asymptotically to the entropy of the sequence with increasing n. This proves that the coding is optimal. Since for optimal coding the code length is 1/probability, and since all code lengths are equal, we may say that, at least in the long limit, the IP motifs have equal probability. Thus, , taking equal weight for nodes in the tree representation, will be deduced as a ratio between the cardinality of the subtrees (number of subnodes) following the node . As the number of subnodes is also the node's share of the probability space (because one codeword is allocated to each node), we see that the amount of code space allocated to a node is proportional to the number of times it occurred.

Relation to Markov models

An interesting relation between Lempel-Ziv and Markov models was discovered by [WIL91] when considering the length of the context used for prediction. In IP every prediction is done in the context of earlier prediction, thus resulting in a sawtooth behavior of the context length. For every new phrase the first character has no context, the second has context of length one, and so on. In contrast, the Markov algorithm makes predictions using a totally flat context line determined by the order of the model. Thus, while a Markov algorithm makes all of its prediction based on 3- or 4-character contexts, the IP algorithm will make some of the predictions from lower depth, but very quickly it will exceed the Markov constant depth and use a better context. To compensate for its poor performance in the first characters, IP grows a big tree that has the effect of increasing the average length of the phrase so that beginnings of the phrase occur less often. As the length of the input increases to infinity, so does the average length, with the startling effect that at infinity it converges to the entropy of the source. In practice though, the average phrase length does not rise fast enough to provide for reliable short-time predictions. On the other hand, it behaves surprisingly well for long sequences. Our experiments show that this IP scheme, along with the appropriate linear representation of music, provides with patterns and inferences that successfully match musical expectation.

Another important feature of the dictionary-based methods is that they are "universal". If the model of the data sequence was known ahead of time, an optimum prediction could be achieved at all times. The difficulty with most real situations is that the probability model for the data is unknown. Therefore one must use a predictor that works well no matter what the data model is. This idea is called "universal prediction" and it is contrasted to Markov predictors that assume a given order of the data model. Universal prediction algorithms make minimal assumptions on the underlying stochastic sources of musical sequences. Thus, they can be used in a great variety of musical and stylistic situations. Our IP based predictor is one such example of universal predictor. This differs also from knowledge-based systems, where specific knowledge about a particular style has to be first understood and implemented [COP96].

3. The Incremental Parsing (IP) algorithm

The IPMotif function computes an associative dictionary (the motif dictionary) containing motifs discovered over a text.

dict is a set of pairs (key, value) where the keys are motifs and values are integer counters. text and motif are ordered lists of untyped objects (we don't restrict to characters). value(dict,motif) retrieves the value associated with motif in dict. W!k notates the list obtained by right-appending object k to list W. Pop(var) returns the leftmost element from the list pointed to by var and advances var by one position to the right.

The text is processed linearly from left to right, object after object, without any backtracking or look-ahead. At any current time, the variable motif contains the current motif W being discovered and the variable text contains the remaining text, beginning just after W. Now a new object k is popped from the text and appended to the right of motif, which value changes to W!k. If W!k is not already in the dictionary, it is added to it and motif is reset to an empty list (), thus being prepared to receive the next motif. The LZ78 compression algorithm would, at that time, output a codeword for W, depending on W's index in the dictionary, along with the object k. Compression would occur because W, which must have been previously encountered, is now output as a simple code. But since we are not concerned with compression, we do nothing more. If W!k is already in the dictionary, we increment the counter associated with it and iterate. By doing this, we compute for each motif W!k the frequency at which object k follows motif W in the text. It is an IP property that, if motif W is in the dictionary, then all its left prefixes are there. So, if for instance motifs ABC, ABCD, ABCE, ABCDE, are discovered at different places, the frequency of C following AB will be equal to 4. Another way to look at it is to consider that, for each motif W in the dictionary, for which there exists other motifs W!k_i in the dictionary, we will easily get the (empirical) conditional probability distribution P(k_i | W) (probability of occurrence of k_i knowing that W has just occurred).

In order to achieve this, we have to transform the motif dictionary into another one, called a continuation dictionary, where each key will be a motif W from the previous dictionary, and the corresponding value will be a list of couples (.. (k, P(k | W)) ..) for each possible k in the object alphabet, representing in effect the empirical distribution of objects following W.

The IPContinuation function computes a continuation dictionary from a motif dictionary.

The function Normalize turns the counters in every element of dict2 into probabilities.

As can be seen in the previous example, a single pass IP analysis on a short text is not sufficient to detect a significant amount of motifs. There is no information on continuations for motif b or motif ba. Due to the asymptotic nature of IP, these motifs will eventually appear when analyzing long texts. Another way to increase redundancy and to detect more motifs is to parse several times the same text using the same motif dictionary, rotating each time the text to the left by one position.

The IPGenerate function generates a new text from a continuation dictionary. Suppose we have already generated a text (a₀ a₁ ... a_n-1). There is a parameter p which is an upper limit on the size of the past we want to consider in order to choose the next object.

4. Resolving the polyphonic problem

The IPGenerate algorithm works on any linear stream of objects. It was successfully tested on linear streams of midi pitches from solo pieces or isolated voices of polyphonic pieces. In order to be able to process polyphony, thus fully capturing rythmical, countrapuntal and harmonic gestures, we had to find a way to linearize multivoice midi data in a way that would musically make sense and take advantage of the IP scheme. The best results were achieved by using a variant of the superposition languages defined by Chemillier & Timis [CHE90].

To understand this, take the 2-voice example shown below.

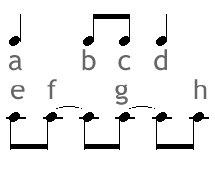
Only the rhythm is notated. Pitch, as well as other relevant information are coded with letters a through h. If we slice time with respect to the common time unit (the gcd of the durations, i.e. the eighth note) we may code the sequence using 2 parallel words:

 

aabcdd

effggh

where the letter x in bold means the continuation of the previous (contiguous) letter x (which is either a beginning symbol or itself a continuation). In order to linearize, we go from the normal alphabet, augmented by continuation symbols, S = {a, b, c, .., a, b, c, ..} to the cross-alphabet SxS. Now the sequence is:

 

(a,e) (a, f) (b, f) (c, g) (d, g) (d, h).

In order to cope with any arbitrary time structure and to optimize the parsing, we use the following variant.

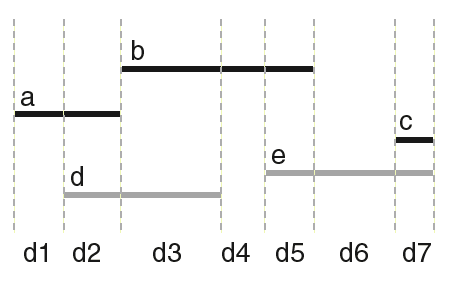
Time is sliced at each event boundary occuring in any voice. A set of durations D = {d₁,..d₇} is thus built. Using the cross alphabet SxSxD we build the linear triplet sequence:

 

(a, -, d₁) (a, d, d₂) (b, d, d₃) (b, -, d₄) (b, e, d₅) (-, e, d₆) (c, e, d₇)

where - denotes the empty symbol (musical rest).

These triplets can easily be packed into 3 bytes numbers if we code only the pitches along with the durations. In order to optimize the duration alphabet, we quantize the original durations into a reasonable set of discrete rhythmic values. The idea is then easily generalized to n-voice polyphony.

5. Experiments

Once a multi-voice midi file is transformed into a linear text based on the cross alphabet, it is presented to the IPMotif/IPcontinuation algorithm. The resulting continuation dictionary can then be randomly walked by IPGenerate to build variants of the original music.

The cross-alphabet representation used has proven to fit decisively into the IP framework. In particular, the continuation symbols encode the fact that certain notes, in certain contexts, have a certain probability of being sustained while other notes are playing on other voices. The result is that countrapuntal gestures, as well as harmonic patterns, tend to be generated in a realistic way with regard to the original. Another caracteristic of IP is that if not only one text but a set of different texts are analyzed using the same motif dictionary, the generation will "interpolate" in a space constituted by this set. This interpolation is not a geometrical one, but rather goes randomly from one model to another when there exists a common pattern of any length and a continuation from the second model is chosen instead the first one.

IPGenerate has been tested, in normal and interpolation mode, over the set of 2-voices Bach Inventions, normalized for tonality and tempo. While the lack of overall harmonic control do not favors consistant harmonic progression in the resulting simulations, these should be seen as "infinite" streams where very interesting subsequences, show original and convincing counterpoint and harmonic patterns.

On the Bach material, we have established empirically that 0 rotation of the original text would lead to a poor, unusable, continuation dictionary; 3-4 rotations are optimal, in that whole phrases from the original may be generated; more rotations do not improve the generation quality. This is certainly due to the way phrases are built from combination of small motifs in this style of music.

In the Jazz domain, a new piece by Jean-Rémy Guedon, miniX, has been created recently at Ircam by the French "Orchestre National de Jazz" with the assistance of Frederic Voisin. In this 20 mn piece, about half of the solo parts were IPGenerated and transcribed on the score.

These experiments were carried-out using OpenMusic, a Lisp-based visual language for music composition [ASS99]. Some results are available at:

 

http://www.ircam.fr/equipes/repmus

 

6. Towards a real-time IP improviser

Once a continuation dictionary, capturing a polyphonic style or style space, has been built in OpenMusic, it can be provided to a real-time interactive program that will use it in order to improvize a voice in response to a human performer playing another voice. As an improvement to known digital improvisers, we want to take advantage of the IP capacity to capture and render convincing polyphonic-contrapuntal gestures.

Implemented in Java, the (still experimental) IPImpro program responds to a performer playing the soprano voice by generating bass notes in accordance with: the continuation dictionary, the past context, and the last note played by the performer. In the following example, where bold symbols denote the sustaining of the previous symbol:

 

sop: a b c c a a b

bass: b b a b a b ?

durs: 2 2 1 1 3 1 ?

the soprano has begun to play b and we have to decide for the bass. If we find, for example, a motif ((a a 3) (a b 1)) with continuation (b b 2) in the continuation dictionary we could decide to ask the bass to play b with a duration of 2 units (as b is a continuation symbol, this would really mean " keep on playing the previous b for 2 units). We have now a real-time specific problem: we don't know if the (human) soprano is actually going to keep on playing b during 2 time units, so we are never sure we have chosen the right triplet. If soprano plays b during one time unit then moves to c, we'll try to find a new triplet that matches the suffix ( ... ((a a 3) (a b 1) (b b 1)), which will eventually cause the bass to stop playing b sooner than expected. If the soprano plays b longer than expected, then we'll consider he is now playing a continuation b of b, and look for a new triplet in accordance with the new context.

As for the OpenMusic version, for each generation step a past context of a predetermined maximum length is checked for a possible continuation in the dictionary. If no continuation is found, one element is cropped on the left of the context and the new context is checked until success is achieved.

Another real-time concern is that the motif dictionary representation used in OpenMusic (table or hash-table) is too costly in retrieval time for fast interaction. IPImpro rather uses a tree representation. Suppose we have, in the dictionary, the following set of pairs

 

context : continuations

 

A : B

AB : B,D

ABD : A,C

C : B

CB : D

D : A,C

This can be easily represented as a tree structure:

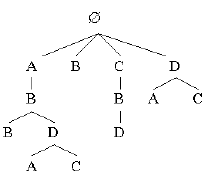
Each node of the tree is associated with a triplet (bass, soprano, duration) notated as a symbol. Paths from the root to a leaf contain, in a condensed representation, available motifs as well as their continuations. Continuation probabilities are easily computed by giving weight 1 to all the leaves, then recursively, bottom-up computing other nodes' weights by summing their children's weights, then normalizing. As long as new continuations are found without needing to crop the current context, a pointer to the tree may move in a contiguous way from node to node and keep track of the last node generated. The new context is simply the path from the root to this node. But when the context has to be cropped (a leaf has been reached) , a new search , starting from the root must be started. If, for instance, the current context was ABDC, the search for a possible continuation in the tree would lead us to examine the A branch down to its leaf (C). Then, as no continuation is found, we would consider the cropped context BDC and examine the B branch. Finally, the context would reduce to C so we would go to the C branch and choose the continuation B. As this research is bounded only by the size of the tree, we might have unpredictable latencies that would endanger real-time interaction.

To overcome this problem, we finally chose a representation that was more costly in space but more effective in time. A tree is built, in the same way, from the continuation dictionary, except the contexts (left side of the arrows) are reversed. So the branch A -B-D becomes D-B-A. At each node N we attach a set of pointers to direct children of the root. They represent the continuations available for the motif matching the path from N up to the root.

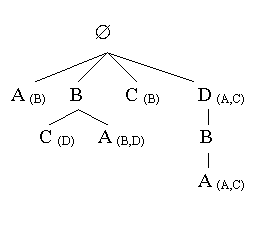
Suppose the current context is ABD. As D is the last object of the context, the pointer is on the D node right under the root. We descend the branch downwards as much as we can, looking for the longest match between the reversed context (DBA) and the successive nodes. We arrive at node A, where we found the continuations (A,C). Suppose we choose to generate C: the new context is ABDC, the pointer moves to the C node under the root. At the next generation step, we'll see immediatly that the new context has no continuation, only it's last suffix C has continuation B.

Now the search is bounded by the maximum depth of the tree, not its total size, which works fine for real-time.

References

[ASS99] Assayag, Agon, Laurson, Rueda. Computer Assisted Composition at Ircam: PatchWork & OpenMusic. Computer Music Journal, to come,1999.

[CHEM90] Chemillier, M, Structure et méthode algébriques en informatique musicale. Doctorat,LITP 90-4, Paris VI, 1990.

[COP96] Experiments in Musical intelligence. Madison, WI:A-R Editions, 1996.

[LZ78] Ziv J, Lempel A, "Compression of individual sequences via variable rate coding", IEEE Trans. Inf. The., 24:5, pp.530-536, 1978.

[WIL91] Williams, R.N, "Adaptive Data Compression", Kluwer Academic Publishers, Norwell, Massachusetts, 1991.