OpenMusic et le problème de la construction de canons musicaux rythmiques.

Moreno ANDREATTA (m_andreatta@hotmail.com)

Augusto AGON (agonc@ircam.fr)

Marc CHEMILLIER (marc@info.unicaen.fr)

Introduction

Parmi les formes musicales qui, à des époques différentes, ont intéressé le plus les musiciens, les théoriciens et, très souvent, les mathématiciens, celle des canons musicaux occupe sans doute une place particulière. Ce terme vient, comme nous l'explique Rousseau - en reprenant Zarlino - par métonymie de certaines règles qui "marquoient comment il falloit chanter ces sortes de fugues (perpétuelles)" ([Rousseau1977], p.107). Les canons musicaux ont été souvent considérés comme le lieu privilégié d'une pensée compositionnelle abstraite et énigmatique [Bizzi1986]. Au cours du XXème siècle, on doit à Olivier Messiaen l'introduction et l'emploi systématique de formes canoniques où l'imitation entre les différentes parties ne concerne que les valeurs rythmiques, indépendamment des autres paramètres (mélodie et harmonie). Le canon rythmique suivant, extrait de la 7ème partie de sa pièce Harawin (Adieu) est intéressant par rapport à la théorie des rythmes non rétrogradables :

fig.1 ([Messiaen1992], p.45)

Si on prend comme unité la double croche, on s'aperçoit facilement que chaque partie est un enchaînement (c.-à-d. juxtaposition) de trois rythmes non rétrogradables :

R₁ = (3, 5, 8, 5, 3)

R₂ = (4, 3, 7, 3, 4)

R₃ = (2, 2, 3, 5, 3, 2, 2).

La distance entre les entrées de ce triple canon est fixe et elle correspond à une croche.

On connaît très bien l'importance, chez Messiaen, des rythmes non rétrogradables : une importance tout d'abord philosophique et symbolique ([Messiaen1992], p.7) mais aussi structurelle, par rapport à une analogie avec les "modes à transpositions limitées". Ce problème nous donne, peut-être, la meilleure introduction au modèle modal et rythmique proposé par le mathématicien roumain Dan Tudor Vuza d'après l'oeuvre théorique du compositeur Anatol Vieru. On trouve l'explication de la complète analogie des rythmes non rétrogradables et des modes à transpositions limitées dans [Messiaen1944], point repris dans ([Messiaen1992], p.9) : "les modes à transpositions limitées réalisent dans le sens vertical (transposition) ce que les rythmes non-rétrogradables réalisent dans le sens horizontal (rétrogradation)". Cette analogie, qui fonctionne très bien au niveau métaphorique, pose des problèmes du point de vue mathématique, comme souligné dans [Mazzola1990].

Le modèle rythmique que nous allons présenter ici permet, au contraire, d'établir une analogie complète (voire un isomorphisme) entre un 'univers modal' (dans un sens très large) et un 'domaine rythmique' (dans un sens, au contraire, plus strict que dans Messiaen, et ce à cause de la notion de périodicité qui entre dans la définition du rythme chez Vuza). Le modèle algébrique de Vuza a des affinités remarquables avec le Système d'Intervalles Généralisés (GIS) du théoricien américain David Lewin [Lewin1987] et la "théorie mathématique de la musique" (MaMuTh) de Guerino Mazzola [Mazzola1990]. La discussion critique de ces liens est l'objet du travail d'un des auteurs dans le cadre du D.E.A. "Musique et Musicologie du XXème siècle" (IRCAM-EHESS) mais ne sera pas évoqué ici.

Aspects mathématiques du modèle de D. Vuza.

Les premiers travaux de Vuza [Vuza1982] représentent une formalisation rigoureuse de la théorie modale d'Anatol Vieru. Dans son ouvrage majeur [Vieru1980], le compositeur roumain avait présenté à un niveau quasi-formel une collection d'opérations et de structures algébriques liées au concept de "modes" (ensembles de classes de hauteurs) et de "classes modales" (classes d'équivalence des modes à isomorphisme près). Pour la construction d'un modèle algébrique de la théorie modale de Vieru, Vuza utilise la notion bourbakiste d'ensemble principal homogène à travers laquelle il obtient une classification des familles principales de classes modales (parmi lesquelles on peut retrouver les modes de Messiaen à transpositions limitées). Un schéma résumant les relations ensemblistes entre les différentes familles de classes modales, avec une discussion sur les approches contemporaines d' autres théoriciens (Babbitt, Halsey et Hewitt...) est contenue dans [Andreatta1997]. L'approche de Vuza de la théorie modale d'Anatol Vieru est bien résumée dans son commentaire de l'oeuvre de Lewin [Vuza1987]. On retrouve ici la thèse avancée dans [Vuza1985], selon laquelle les résultats obtenus en général pour des ensembles principals homogènes trouvent une application naturelle dans son modèle du rythme périodique. En effet, le lien entre modèle mathématique du rythme et théorie modale "est fourni par l'existence des bijections canoniques entre certains sous-ensembles de rythmes (respectivement classes rythmiques) et l'ensemble des modes (respectivement classes modales) dans un système tempéré à n degrés" ([Vuza1985], p.73).

À la différence du modèle rythmique proposé par Lewin, Vuza se concentre sur un objet musical très particulier, le rythme périodique qui est formalisé comme un sous-ensemble périodique et localement fini du corps Q des nombres rationnels, plus précisement ([Vuza1991], p.38) un sous-ensemble R de Q (éventuellement vide) tel que:

1. L'ensemble S_R des nombres rationnels positifs t tels que t + R = R est non vide
2. Pour tous éléments a, b du groupe additif Q tels que a<b, l'ensemble RÇ [ a,b[ est fini.

Par analogie avec les classes modales (qui à partir de [Vuza1991] seront indiquées simplement comme "classes de translation" d'un groupe G fixé), on a ainsi la définition de la classe rythmique R comme la classe de translation d'un rythme R par rapport au groupe additif Q ([Vuza1991], p.39). L'analyse complète de la correspondance bijective entre les ensembles de classes de translation et certaines classes rythmiques ne peut pas être abordée ici. On renvoie, par exemple, à ([Vuza1991], p.43).

Les conséquences sont, au contraire, plus facilement analysables. Il y a tout d'abord une importance pratique, si on observe que "dans certaines situations compliquées du point de vue rythmique, les calculs sur les classes de translations sont plus faciles que les opérations directes sur les classes rythmiques" ([Vuza1991], p.42). Mais l'importance fondamentale de cette correspondance est liée au fait qu'elle donne la base théorique pour l'étude d'une famille particulière de canons musicaux rythmiques, liés, d'une façon surprenante, à un ancien problème de "pavage".

Groupes de Hajós et Canons rythmiques.

Parmi les familles de canons rythmiques décrites par Vuza dans la série d'articles parus dans Perspectives of New Music, il y a toute une classe de canons qui sont, depuis plusieurs années, l'objet d'études différentes (voir [Vuza1991], [Vuza1995], [Andreatta1997]).

Voilà un exemple :

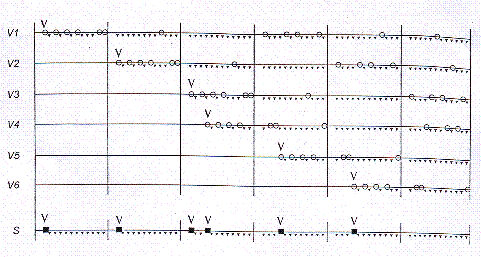
fig.2 [Andreatta1997]

Il s'agit d'un canon rythmique (infini) en 6 parties représenté graphiquement selon le modèle originel de Vuza. On a marqué le début de chaque voix avec un accent et les attaques sont indiquées par des petits cercles vides. Sans prendre en compte tous les paramètres liés à un canon rythmique, on peut noter que ceci est bien défini quand on a donné :

1. Le nombre de voix qui forment le canon.
2. La classe rythmique (dite "ground class" et indiquée avec la lettre R) d'une voix (voire de toutes les voix)
3. La classe rythmique (dite "metric class" et indiquée avec la lettre S) qui organise les entrées des différentes voix (correspondantes aux carrés pleins).

La structure du canon précédent est liée à une factorisation du groupe cyclique Z_n (n=108) comme une somme de deux sous-ensembles ("supplementary sets") non-périodiques. On peut démontrer qu'une telle factorisation n'est pas possible si le groupe cyclique possède la propriété de Hajós [Andreatta1997]. On découvre que les groupes de Hajós sont liés à un problème de pavage ("tiling") qui remonte à fin de XIXème siècle et connu comme la conjecture de Minkowski. Dans sa forme géométrique (1907) elle affirme que :

"Dans un pavage [lattice tiling] d'un espace à n-dimensions par des cubes unité, il y a au moins un couple de cubes qui ont en commun une face entière de dimensions n-1" (voir [Stein1994], p.22).

fig.3

La conjecture, judicieusement exprimée sous la forme d'une conjecture équivalente sur des groupes abéliens finis, a été résolue par le mathématicien hongrois G. Hajós en 1941. Il est surprenant de voir que le lien entre conjecture de Minkowski et canons rythmiques n'a été établi que très récemment [Andreatta1997].

Canons rythmiques dans l'environnement OpenMusic [Assayag&Agon 1996].

Le canon montré dans la . 2 est un exemple très particulier de canon rythmique. Après l'entrée de la dernière voix, on finit par entendre une pulsation régulière où chaque instant temporel est rempli par une attaque (et une exactement) d'une voix. Les 6 voix sont, ainsi, complémentaires, l'une de l'autre. De plus, si on indique par Per(R) (et respectivement Per(S)) le période de la classe rythmique R (résp. S) du canon (c.-à-d. le nombre de pulsations après lesquelles S et R répètent leur pattern rythmique), on a la propriété suivante :

Per(R) = Per(S) = 108.

Suivant Vuza nous appelons ces canons qui ont la propriété précédente canons réguliers complémentaires de catégorie maximale.

Bien que Vuza ait fourni dans [Vuza1991] et [Vuza1995] un algorithme "algébrique" pour obtenir tous les canons rythmiques ayant cette propriété, il nous semblait que ces problèmes n'avaient jamais trouvé une application satisfaisante dans le domaine de l'informatique musicale. C'est pour cette raison que nous avons commencé à étudier le problème avec le logiciel OpenMusic de l'IRCAM. Tout d'abord, nous avons établi la liste de valeurs de n correspondantes aux groupes cycliques Z_n qui ne possèdent pas la propriété de Hajós. Voilà la liste pour les entiers inférieurs de 1000. Elle est obtenue d'après ([Vuza1991], p.33) en supprimant de la liste des entiers de 1 à 1000 tous les entiers qui sont (1) puissance d'un nombre premier, (2) produit d'une puissance d'un nombre premier par un autre nombre premier, (3) produit des carrés de deux nombres premiers distincts, (4) produit de deux nombres premiers par un troisième nombre premier ou son carré, (5) produit de quatre nombres premiers :

(72 108 120 144 168 180 200 216 240 252 264 270 280 288 300 312 324 336 360 378 392 396 400 408 432 440 450 456 468 480 500 504 520 528 540 552 560 576 588 594 600 612 616 624 648 672 675 680 684 696 700 702 720 728 744 750 756 760 784 792 800 810 816 828 864 880 882 888 900 912 918 920 936 945 952 960 968 972 980 984 1000)

fig.4

On sait ([Vuza 1995], Prop. 4.3 p.95) que tout n de ce type peut être ainsi décomposé :

n = p₁·p₂·n₁·n₂·n₃

où:

• p_i sont premiers (différents)
• p₁ · n₁ _p₂ · n₂ = 1 (c.-à-d. les p_i · n_i sont relativement premiers entre eux)
• n_i _2 , 1 _ i _3.

La ure 5 suivante montre que dans la majeure partie des cas la décomposition n'est pas unique. Ce fait a des conséquences importantes sur le nombre de voix admissibles pour de tels canons ( par exemple pour n=120 on a deux solutions).

72 : { (2 3 2 3 2) }

108 : { (2 3 2 3 3) }

120 : { (2 3 2 5 2), (2 5 2 3 2) }

144 : { (2 3 2 3 4), (2 3 4 3 2) }

168 : { (2 3 2 7 2), (2 7 2 3 2) }

180 : { (2 3 2 5 3), (2 3 2 3 5), (2 3 5 3 2), (2 5 2 3 3 ) }

200 : { (2 5 2 5 2 }

216 : { (2 3 2 3 6), (2 3 2 3 6), (2 3 4 3 3 ) }

240 : { (2 3 4 5 2), (2 3 2 5 4), (2 5 2 3 4), (2 5 4 3 2 ) }

252 : { (2 3 7 3 2), (2 3 2 3 7), (2 3 2 7 3), (2 7 2 3 3 ) }

264 : { (2 3 2 11 2), (2 11 2 3 2 }

270 : { (2 3 5 3 3) }

280 : { (2 5 2 7 2), (2 7 2 5 2 ) }

288 : { (2 3 4 3 4), (2 3 2 3 8), (2 3 8 3 2 ) }

300 : { (2 3 2 5 5), (2 5 2 5 3), (2 5 2 3 5), (2 5 3 5 2 ) }

312 : { (2 3 2 13 2), (2 13 2 3 2 ) }

324 : { (2 3 2 3 9), (2 3 2 9 3 ) }

336 : { (2 3 2 7 4), (2 3 4 7 2), (2 7 2 3 4), (2 7 4 3 2 ) }

360 : { (2 3 10 3 2), (2 3 4 5 3), (2 3 4 3 5), (2 3 2 5 6), (2 3 2 3 10),

 (2 3 5 3 4), (2 5 2 3 6), (2 5 2 3 6), (2 5 4 3 3) }

... ...

fig.5

L'étape suivante consiste à établir, pour tout n de ce type, une factorisation du groupe cyclique Z_n comme somme de deux sous-ensembles M et N supplémentaires (c.-à-d. tels que (cardM)(cardN) = cardZ_n = n et que tout x de Z_n est représentable (d'une façon unique) comme somme d'un élément de M et d'un élément de N). Le calcul a été implémenté en OpenMusic par Carlos Agon et les deux ures 6 et 7 suivantes montrent un exemple de cette implémentation. Les ensembles M et N obtenus ont respectivement comme cardinalité·n₁·n₂ ·et p₁·p₂·n₃.

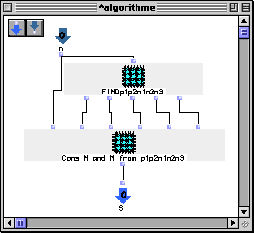
fig.6

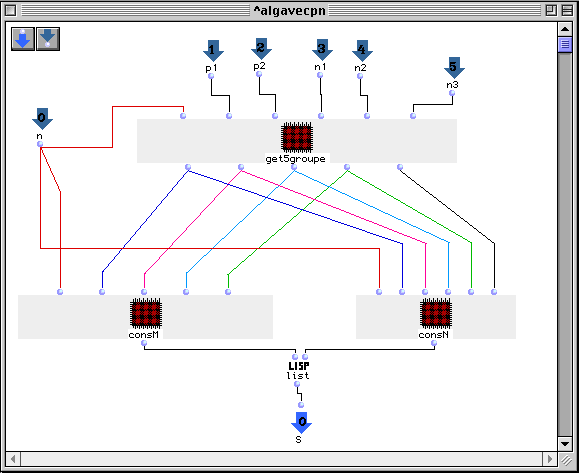
fig.7

On obtient ainsi les deux classes rythmiques, respectivement "ground class" R et "metric class" S du canon ([Vuza1985, p.82]). Le nombre de voix est la cardinalité de l'ensemble M, c.-à-d. n₁·n₂. Il faut souligner que bien que la décomposition de n soit parfois unique (comme pour n=72) on obtient cependant des factorisations différentes (M,N) pour le même groupe cyclique (d'où des canons rythmiques différents mais ayant tous le même nombre de voix). Pour le canon de la ure 2, on a :

M = {39, 51, 63, 66, 78, 90}

N = {16, 18, 20, 22, 26, 27, 36, 52, 56, 58, 62, 72, 81, 88, 90, 92, 94, 98}

d'où les valeurs rythmiques correspondantes :

R = [2, 2, 2, 4, 1, 9, 16, 4, 2, 4, 10, 9, 7, 2, 2, 2, 4, 26]

S = [12, 12, 3, 12, 12, 57]

obtenus à partir de la différence des éléments consécutifs [Andreatta1997 , p. 28].

La ure 8 suivante montre un exemple de canon musical à 6 voix dont l'organisation des hauteurs est modelée d'après une cadence employée par I. Stravinskij dans sa Sonate pour piano (1924).

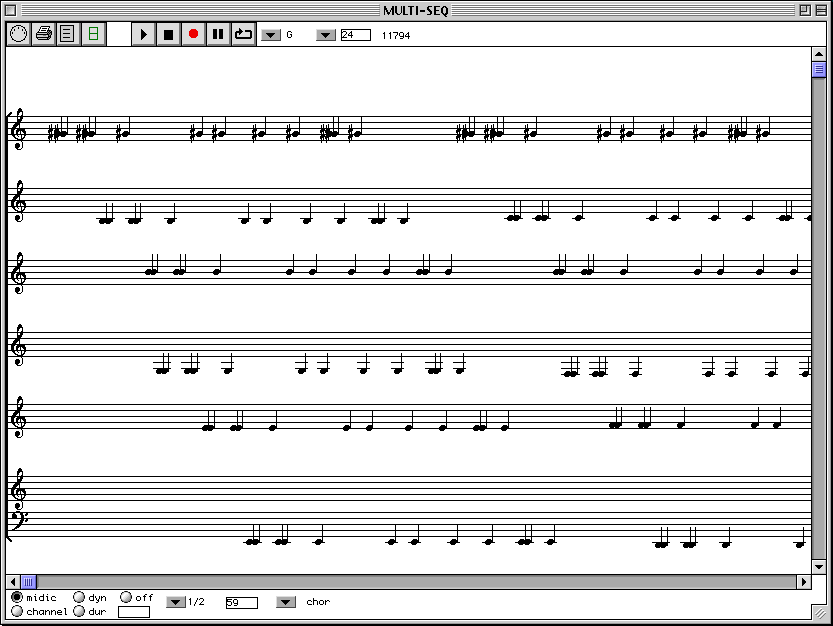
fig.8

OpenMusic peut donc être employé pour mieux comprendre la structure de cette famille très riche de canons musicaux. En particulier, en reprenant l'exemple de Harawin, on est conduit à affaiblire une hypothèse appelée (un peu pompeusement) la M-Conjecture ([Andreatta1997], p.30). Elle affirmait que dans un canon régulier complémentaire de catégorie maximale, la classe métrique est - au moins d'une valeur initiale ou terminale - un rythme non-rétrogradable dans le sens de Messiaen. La nouvelle conjecture affirme que pour toute n correspondant aux groupes cycliques Z_n qui ne possèdent pas la propriété de Hajós il y a au moins un canon régulier complémentaire de catégorie maximale dont la classe métrique S est -au moins d'une valeur initiale ou terminale- un rythme non-rétrogradable (c'est un résultat qui ne semble pas dériver, directement, de la théorie de Vuza).

Remerciements.

Merci à Gérard Assayag d'avoir donné la possibilité de présenter une partie des résultats obtenus dans les 'Séminaires de Recherche' de l'IRCAM.

Bibliographie: