ANNEXE I.
Situation dans OpenMusic.
Nous exposons dans cette annexe la façon dont on a intégré Situation à OpenMusic en tant qu'une librairie. Situation est un langage pour la composition musicale, basé sur les contraintes [RuBo98]. Avant d'illustrer cette interaction, à l'aide de quelques exemples, nous allons introduire les concepts de base dans Situation (pour une description complète voir [BoRu97]).
II.1 Description.
Dans Situation, les objetssont construits à partir de deux notions : les points et les distances. En ce qui concerne le domaine musical, Situation a été optimisé pour la résolution des problèmes harmoniques et rythmiques. Dans le premier cas, les objets de base sont les accords, définis par un nombre de points (les hauteurs) espacés selon certaines distances (les intervalles) mesurés dans une unité de base (demi-ton, quart de ton, etc.). Pour les problèmes rythmiques, l'objet de base est appelé le plan rythmique. Les points constituent des points d'articulation. Les intervalles définissent les durées. L'unité peut être choisie parmi des figures rythmiques telles que la noire, la croche, etc. L'intérêt de Situation, dans la composition, provient de la possibilité de construire des objets d'ordre supérieur (séquence d'accords ou polyrythmies). Ces objets sont contraints à des relations entre n'importe quels points de n'importe quels objets. Situation se fonde sur la notion d'objet et non d'élément (un élément ,une hauteur par exemple, est un objet ne comportant qu'un seul point et aucune distance interne).
La définition d'un problème dans Situation se fait en deux étapes : la définition du "domaine" de possibilités et la définition des "contraintes".
- Pour la définition du domaine dans le cas d'une application musicale, il faut spécifier pour un problème harmonique : le nombre d'accords, l'ensemble des hauteurs possibles, le nombre de hauteurs dans chaque accord, les intervalles possibles entre les hauteurs d'un même accord et les intervalles possibles entre des hauteurs d'accords différents. Pour un problème rythmique : le nombre de plans rythmique, l'ensemble des points d'articulation possibles, le nombre de points d'articulation dans chaque plan rythmique, les durées possibles entre des points d'un même plan rythmique et les durées possibles entre des points de plans rythmiques différents.
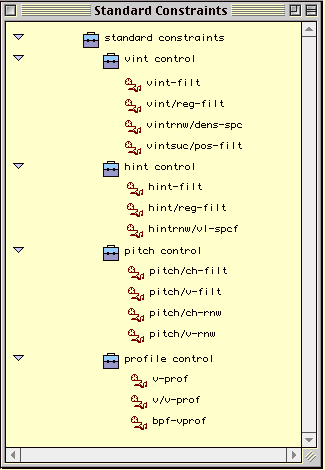
- Il existe quatorze contraintes définies par le système. Elles sont classées en fonction de l'attribut sur lequel elles agissent : les distances, les points ou les profils. Les contraintes sur les profils permettent de contrôler l'évolution d'une voix seule ou d'une voix par rapport à une autre. Nous entendons par voix la mise en relation des points appartenant à des objets différents.
La figure suivante montre les contraintes prédéfinies.

Figure II.1 Contraintes prédéfinies dans Situation.
L'utilisateur peut définir ses propres contraintes au moyen d'une librairie de modules prévue à cet effet. L'inclusion de Situation dans OpenMusic garantit une définition totalement graphique des contraintes, car les fonctions et les patches sont citoyens de première classe.
En général, le domaine d'une variable ne contient pas des valeurs simples, comme des entiers par exemple, mais plutôt des ensembles de valeurs simples. Ces ensembles, sont calculés avant l'exploration et constituent l'espace de possibilités qui doit être filtré par les contraintes. Ce choix de représentation s'avère plus adapté aux problèmes musicaux pour lesquels Situation a été conçue [BoRu98]. Situation permet aussi d'établir des hiérarchies à l'intérieur d'un domaine. Chaque niveau de la hiérarchie est défini par rapport à une fonction particulière. Par exemple si l'on hiérarchise, au moyen de la fonction +, le domaine des séquences de distances, les séquences [1, 7, 5] et [9, 4] sont regroupées dans un même sous-ensemble, identifiés par la valeur 13. Ainsi les contraintes peuvent porter soit sur les "vraies données" - les séquences -, soit sur les valeurs projetées.
Une fois le problème défini, la résolution s'effectue par l'évaluation de la boîte csolver qui déclenche la recherche d'une ou plusieurs solutions au problème spécifié par ses entrées.
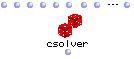
Figure II.2
Les entrées de cette boîte, de gauche à droite spécifient :
1. Le nombre d'objets qui font partie de la solution (dans le cas d'un problème harmonique le nombre d'accords cherchés).
2. Le nombre de points pour chaque objet (notes dans un accord).
3. Les distances possibles pour chaque objet (les intervalles d'un accord).
4. Le Domaine des points pour chaque objet (l'ambitus de chaque accord).
5. Une liste de contraintes du problème.
6. Le nombre de solutions souhaité (-1 pour toutes).
7. La définition des objets en extension (une liste d'accords pour chaque accord dans la séquence). Cette entrée est optionnelle.
8. Force le moteur de résolution à trouver une autre solution en gardant tous les objets déjà trouvés mais un cherchant une nouvelle valeur pour l'objet spécifié par cette entrée. Cette entrée est optionnelle.
9,... Chacune de ces entrées représente un nouveau sous-problème qui est ajouté au problème courant déjà supposé résolu.
Étant donné la généralité du moteur de résolution l'évaluation du module csolver se présente sous forme d'une liste de liste de nombres qu'il s'agit de traduire.
Pour les deux types de problèmes musicaux il existe deux modules permettant de construire les solutions : ch-sol (harmonic solution) pour les problèmes harmoniques et rtm-sol (rhythmic solution) pour les problèmes rythmiques. Nous concluons cette annexe avec un exemple de chaque type de problème.
II.2 Un exemple harmonique.
La figure II.3 montre un patch OpenMusic définissant un problème de contraintes pour l'harmonisation du début de Syrinx de Debussy. La mélodie est tirée d'un fichier MIDI qui sert de référence à la boîte (A).
Les entrées de la boîte csolver, de gauche à droite, contiennent les valeurs :
1. 16. Ce qui signifie qu'on va construire 16 accords.
2. (0_15 (36 84)). Cette liste force les notes à appartenir à l'ambitus définit par Do2 et Do5.
3. (0 (3 3) 1_7 (interp (3 3) (7 7)) 7_13 (interp (7 7) (3 5)) 13_15 (interp (3 5) (3 4)). En ce qui concerne la densité, le premier accord doit contenir 3 notes, les sept accords suivants, une densité définie par une interpolation linaire entre 3 et 7 notes, finalement les 8 derniers accords ont une densité définie par une interpolation entre 7 et 3 ou 5 notes.
4. (0_7 ((4 3)) 8_15 ((4 6 10))). Les huit premiers accords ne contiendront que des tierces majeures et mineures superposées et les huit derniers des tierces majeures, des quartes augmentées et des septièmes mineures.
La liste qui définissant les deux contraintes du problème est construite par les patches voice-profile et force-voice.
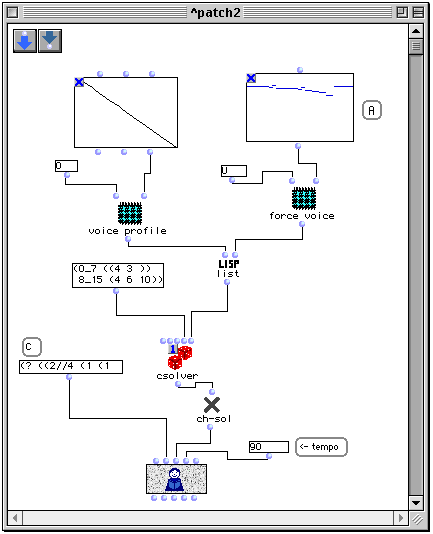
Figure II.3
Le patch force-voice (figure II.4) extrait la liste des hauteurs du fichier Midi passé comme deuxième paramètre (input1). Cette liste et le nombre de voix (Upper) sont passés à la boîte omloop qui à son tour construit une expression contraignant les hauteurs de la voix supérieure aux valeurs du fichier. La contrainte est construite et retournée en utilisant la boîte pitch/v-filt.
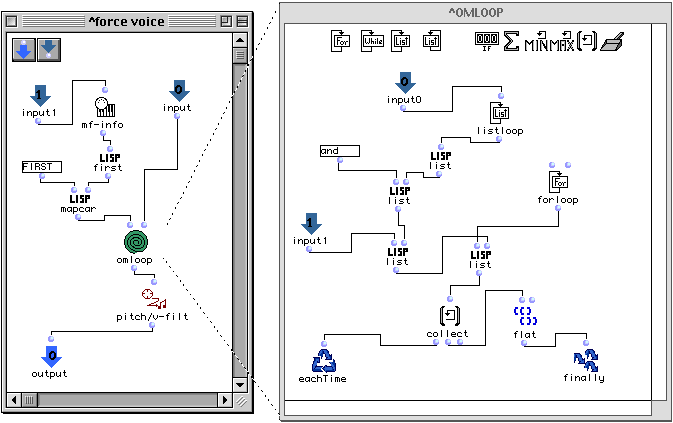
Figure II.4
Le patch voice-profile (figure II.5) force la voix la plus grave à être monotoniquement décroissante. La boîte v-prof reçoit la liste (0_15 (0 (-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1))) et construit une contrainte qui impose pour la voix basse (0) une direction descendante (-1). En fait ce patch est capable de construire une contrainte pour n'importe quel nombre de voix (input) à partir d'une fonction par segments quelconque (input1).
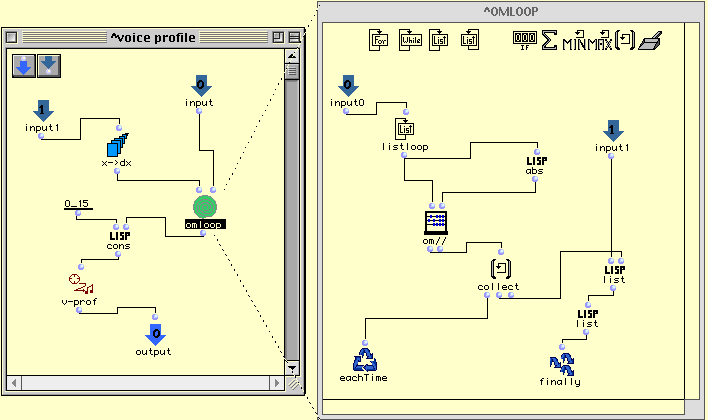
Figure II.5
Une fois la solution trouvée (si elle existe) la boîte ch-sol prend la solution de csolver et la transforme en une liste d'objets OpenMusic, des instances de la classe chord. Une solution du problème est illustrée dans la figure suivante (le rythme est construit à la main, voir C dans la figure II.3) :
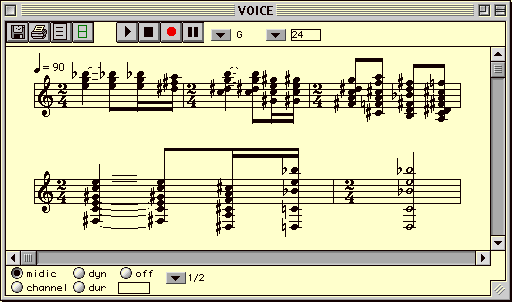
Figure II.6
II.2 Un exemple rythmique.
Le patch de la figure II.7 calcule trois objets rythmiques (voix) dont les points correspondent à des motifs rythmiques.
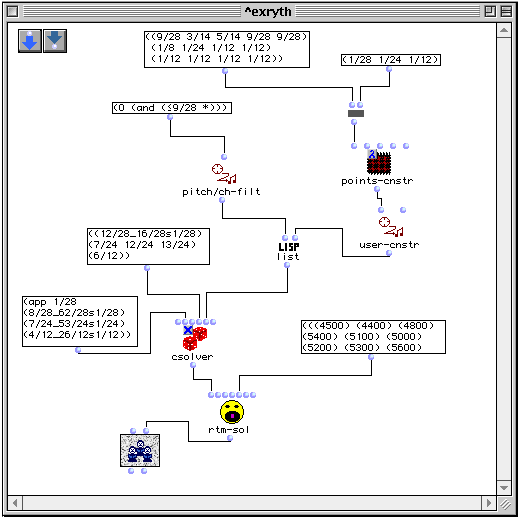
Figure II.7
Les entrées de la boîte csolver, de gauche à droite, contiennent les valeurs :
1. 3 . Trois voix à calculer .
2. (app 1/28 (8/28_62/28s1/28) (7/24_53/24s1/24) (4/12_26/12s1/12). L'approximation minimum est de 1/28 (la double croche de septolet). La première voix est mesurée en doubles croches de septolets et peut contenir des points compris entre 8/28 et 62/28 La deuxième voix est mesurée en double croche de sextolets avec des valeurs comprises entre 7/24 53/24. Finalement, la troisième voix ne peut utiliser que les croches de triolet comprises entre les 4/12 26/12.
3. ((5) (4) (4)). Les trois objets comportent successivement 5, 4 et 4 points d'articulation.
4. ((12/28_16/28s1/28) (7/24 12/24 13/24) (6/12)). Spécifie les distances internes possibles pour chaque voix : entre 12 et 16 doubles-croches de septolet pour la première, entre 7 et 12 doubles-croches de sextolet pour la seconde, et 6 croches de triolet pour la dernière.
La liste qui définissant les deux contraintes du problème est construite par les boîtes pitch/ch-filt et user-cnstr.
La boîte pitch/ch-filt force les points d'un objet à s'accorder avec le motif passé comme paramètre. Dans notre exemple, la liste (0 (and (²9/28 *))) force la durée de la première note du premier motif à être inférieure à 9/28.
La boîte user-cnstr permet à l'utilisateur la construction d'une contrainte définie par un prédicat (première entrée) et par une liste spécifiant les objets que le prédicat contraint (deuxième entrée). Le prédicat est implémenté sous la forme d'une boîte de patch avec visualisateur d'état en mode lambda.
Le patch de la figure II.8 permet de contrôler qu'aucun motif ne se recouvrira lorsque les points des trois objets seront instanciés (la programmation de ce prédicat nécessite évidemment de connaître la taille des motifs et l'unité de distance de chaque objet : celles-ci apparaissent comme arguments de la boîte).
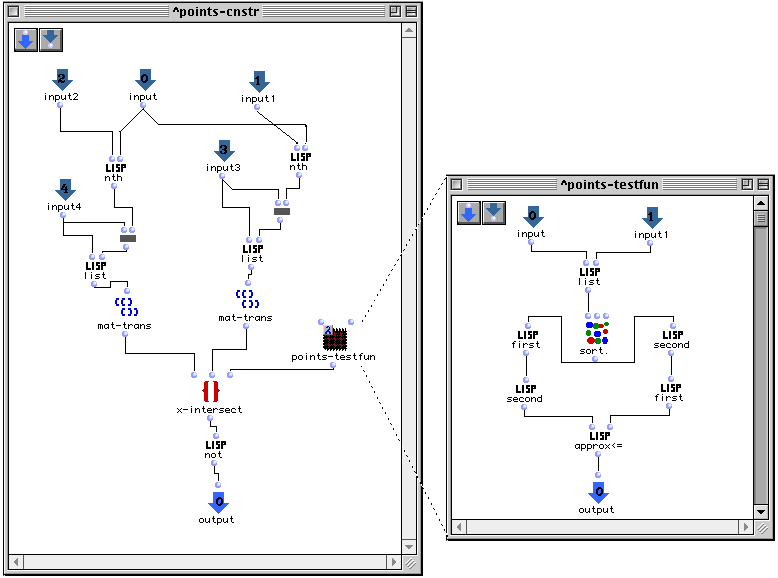
Figure II.8
Une fois la solution trouvée (si elle existe) la boîte rtm-sol prend la solution de csolver et la transforme en une instance de la classe OpenMusic poly. Une solution du problème est illustrée dans la figure suivante (les hauteurs sont données à la main, dans cet exemple, cette liste est aussi le résultat d'un autre problème de contraintes dans Situation).

Figure II.9
Annexe II.
Patchs et sélection de méthodes.
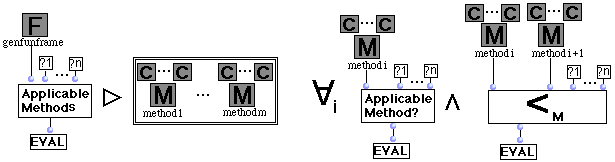
II.1 Règles concernant la sélection d'une méthode lors de l'évaluation d'une fonction générique.
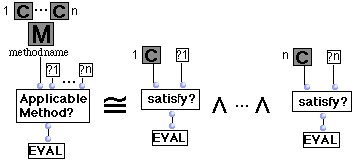
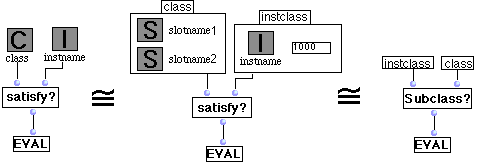
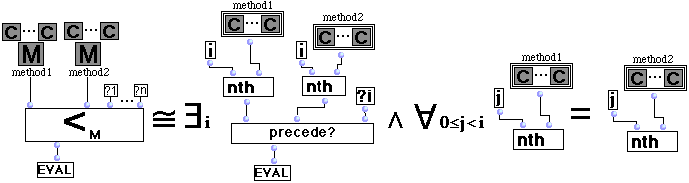
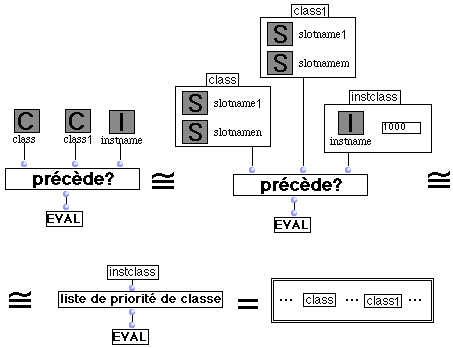
II.2. Patch Bpf2cs.
Le patch bpf2cs a une entrée input et une sortie output.) Ce patch définit une fonction qui reçoit pour paramètre une fonction par segments (bpf) et construit une séquence d'accords retournée lors de la sortie (chaque accord est consistitué d'une note).
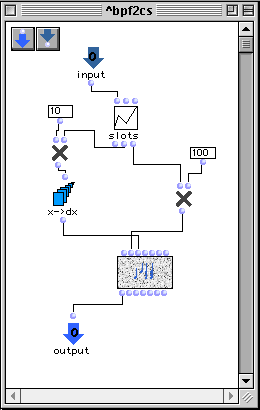
Les points x de la bpf correspondront aux points d'attaque de chaque accord dans la séquence. La fonction x->dx calcule une liste d'intervalles à partir d'une liste de points.
Les points y de la bpf définissent les hauteurs de chaque note constituant l'accord. Ces valeurs sont converties en midicents, tout simplement en les multipliant par 100.
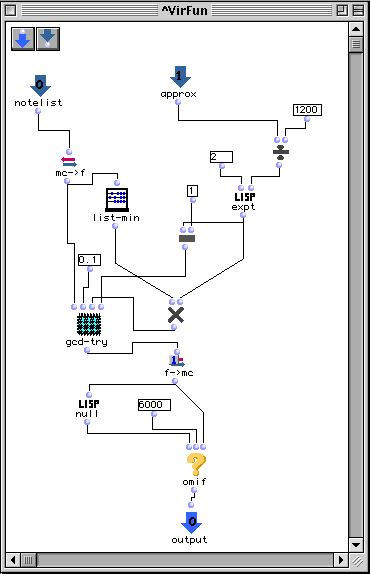
II.3 Patch Virfun.
Ce patch calcule la fondamentale virtuelle d'un accord. La liste
de notes exprimées en midicents est traduite en
fréquences grâce à la boîte
mc->f. L'entrée approx est un facteur de
tolérance utilisé pour éviter de trouver des
fondamentales virtuelles trop graves. L'expression 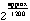 retourne le ratio
entre deux fréquences séparées par approx
(approx est un intervalle exprimé en midicents).
retourne le ratio
entre deux fréquences séparées par approx
(approx est un intervalle exprimé en midicents).
La fonction Lisp qui calcule le gcd des valeurs values avec une tolérance de grid-ratio,
(defun tolerant-gcd (values grid-ratio)
"floating gcd with tolerance grid-ratio around the values."
(labels ((grid-above (val) (* val (1+ grid-ratio)))
(grid-below (val) (/ val (1+ grid-ratio)))
(gcd-try (values gcd-min gcd-max)
(when (<= gcd-min gcd-max)
(ifnot values
(/ (+ gcd-min gcd-max) 2.0)
(let* ((val-below (grid-below (first values)))
(val-above (grid-above (first values)))
(quo-min (ceiling (/ val-below gcd-max)))
(quo-max (floor (/ val-above gcd-min))))
(do* ((quotient quo-min (1+ quotient)) (gcd-interval))
((> quotient quo-max) nil)
(setf gcd-interval
(gcd-try (rest values)
(max gcd-min (/ val-below quotient))
(min gcd-max (/ val-above quotient))))
(when gcd-interval
(return-from gcd-try gcd-interval))))))))
(gcd-try values .1 (grid-above (apply 'min values)))))
Peut être implémentée graphiquement par les patchs suivantes :
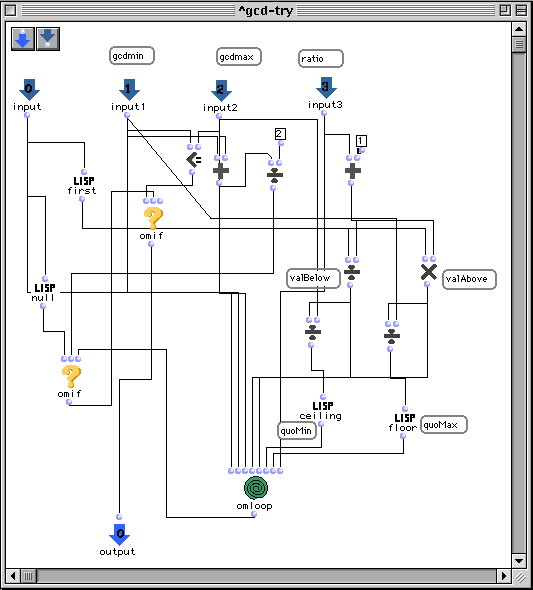
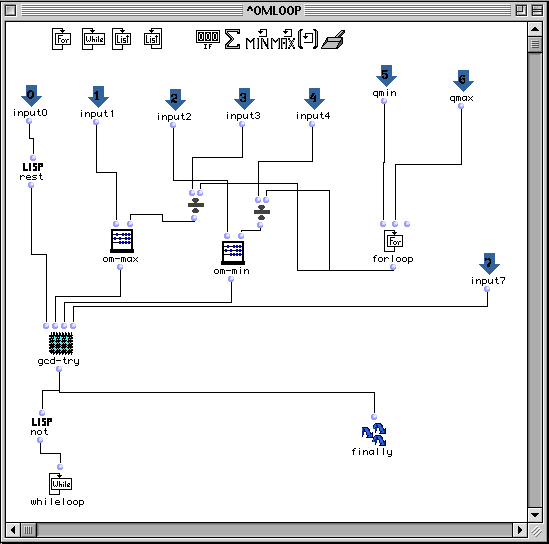
II.4 Patch list2Maq.
Le patch list2maq reçoit une liste d'entiers ou une liste de listes. Indépendamment de son entrée, ce patch retourne une nouvelle maquette qui est construite par la factory appelée ·ommaquette.
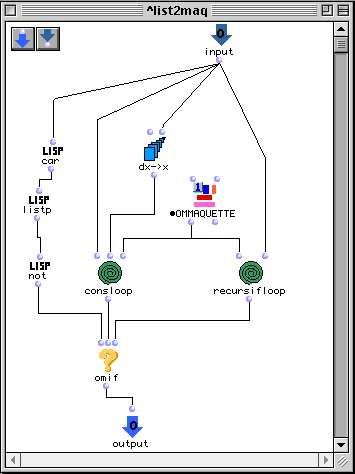
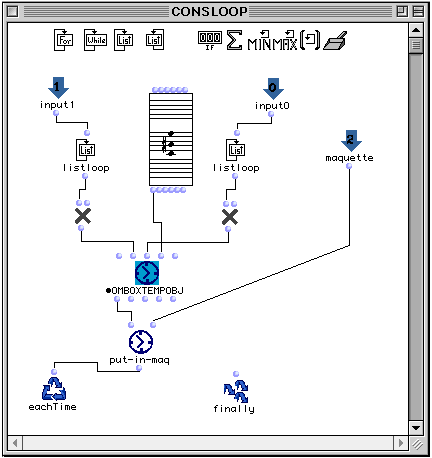
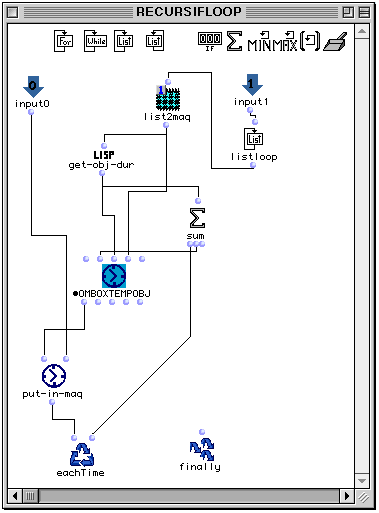
Si l'entrée est une liste d'entiers, le patch remplit la maquette avec de nouvelles boîtes temporelles. Cette tache est remplie par la boîte cosnloop. Dans le cas où la liste est une liste de liste, la maquette sera remplie en utilisant la boîte recursifloop.
II.5 Patch de clonage d'une boîte temporelle.
Le patch de la figure suivante fait une copie d'une instance de la classe OMBoxTemp récupérée dans la boîte appelée input.
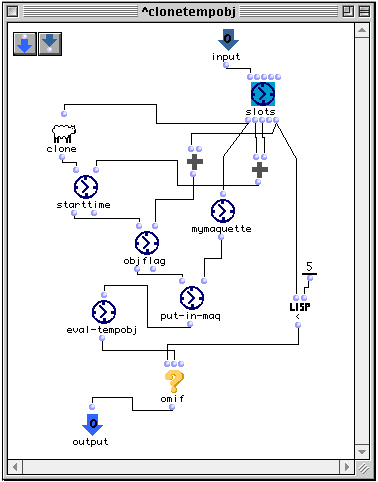
La boîte omif vérifie que le champ flag de la boîte temporelle originale est inférieur à 5. Si c'est le cas, une copie est construite (boîte clone) et sur laquelle s'effectuent certaines modifications :
II.6 Protocole des objets temporels.
Une instance est un objet temporel si la méthode allowed-in-maq-p appliquée à l'instance retourne T.
(defmethod allowed-in-maq-p ((self t))
"T si l'objet peut être inclus dans une maquette.")
Si l'instance peut être inclue dans la maquette, la classe de l'instance doit aussi implémenter les méthodes suivantes :
(defmethod get-obj-dur ((self t)))
"Retourne la durée de self exprimée en millième de secondes.")
(defmethod Play ((self t) at)
"Joue l'objet self au temps at.")
(defmethod allow-strech-p ((self t) (factor number))
"T si l'objet peut être stretché.")