et les types record par
. Les expressions suivantes
définissent les classes 2DPoint et 2DColorpoint.OpenMusic, un environnement de CAO.
Nous détaillons dans ce chapitre les différents choix de conception et d'implémentation pour notre environnement de CAO. Nous essayerons de répondre aux objectifs mentionnés dans le chapitre 1, tout en gardant en tête le souhait d'une applicabilité à moyen terme de notre environnement. Nous divisons ce chapitre en trois grandes parties qui correspondent aux trois niveaux d'accès d'OpenMusic pour l'utilisateur, à savoir : un langage de programmation ; un environnement de programmation ; un framework pour la CAO.
Comme il est dit dans le chapitre 1, OpenMusic a pour but l'intégration de divers modèles de programmation dans un même langage de programmation. Nous travaillons sur les modèles suivants :
- Le modèle fonctionnel
- Le modèle objet
- Le modèle par contraintes
- Le modèle visuel.
Le modèle visuel a un statut particulier dans la mesure où il "enveloppe" les autres. Le modèle par contraintes n'a pas encore été complètement traité, pour l'instant il se limite à une intégration de la librairie Situation dans OpenMusic.
La première décision à prendre a reposé sur le choix entre la conception d'un langage de programmation, suivi du développement d'un interprète ou d'un compilateur pour ce langage, ou l'adoption pour nos besoins d'un langage existant. Le groupe AVISPA qui mène des recherches parallèles aux nôtres a opté pour la première option : " L'objectif du projet AVISPA est la conception et implémentation d'un langage visuel qui combine les paradigmes orienté-objets et de programmation par contraintes. La conception d'un nouveau langage de programmation demande la définition de sa syntaxe (forme correcte d'écriture d'un programme) ainsi que de sa sémantique (la signification d'un programme). En addition, pour l'implémentation, on doit définir une machine abstraite (ou un modèle opérationnel) qui soit suffisamment proche de la machine Von Neuman pour que l'exécution soit efficace. Ce modèle doit posséder des structures de haut niveau pour que l'implémentation soit la plus directe possible. ". Nous avons opté pour le deuxième choix, donc pour un compromis qui nous permet de faire l'économie de la conception d'un langage de base et nous offre la possibilité de nous consacrer à la création d'un modèle et d'un langage visuel original et bien adapté pour la musique. Cette option "réaliste" est aussi justifiée par la taille réduite de l'équipe.
Il existe des langages multi-paradigmes, tels que OZ [Smol95], ML_ART [Rémy95] et Baby-Module-3 [Abad93]. Ces langages n'étaient cependant pas bien adaptés à nos objectifs pour les raisons suivantes :
- Diffusion limitée et non disponibilité sur les plate-formes utilisées par les compositeurs.
- Manque de librairies graphiques puissantes.
- Manque de librairies musicales, notamment pilotes MIDI, notation musicale, etc.
Nous avons choisi de construire OpenMusic "au dessus" du langage CLOS. Le choix de CLOS obéit principalement aux raisons suivantes :
- C'est un langage fonctionnel et objet puissant, bien défini, disposant d'un modèle formel solide [Cast98].
- CLOS et Common Lisp ont fait l'objet d'une normalisation internationale et ont un excellent degré de portabilité [Stee98].
- Des librairies graphiques orientées objet existent sur toutes les plate-formes.
- Une énorme quantité de savoir-faire en informatique musicale (et notamment toute l'expérience de l'Ircam depuis PreForm et PatchWork) est associée à ce langage.
- La réflexivité et le protocole de méta-objets facilitent le type d'extension que nous voulons réaliser.
- Le modèle de fonctions génériques constitue une bonne intégration des aspects fonctionnel et objet.
Cependant, nous souhaitons réaliser plus qu'une simple interface visuelle pour CLOS ; nous nous proposons de définir formellement le langage visuel de telle sorte qu'il soit envisageable de l'implémenter sur d'autres langages.
2.1.1 Modèles de calcul pour les langages à objet.
Nous avons choisi de manière intuitive la programmation par
objets comme modèle de base sur lequel nous intégrons
les autres modèles de programmation. Cependant, il est apparu
très vite un premier inconvénient, à savoir :
à la différence du modèle fonctionnel et par
contraintes dont les modèles de calcul sont bien
définis (lambda calcul et logique de premier ordre
respectivement), la définition de la sémantique des
langages par objets reste un problème ouvert. Parmi les
premiers travaux qui essayent de définir une sémantique
de langages par objets, l'un des plus connus est l'extension du
lambda calcul typé dans [CaWe85]. Dans cet article, la
représentation d'objets se fait à l'aide de
quantificateurs sur des types de deuxième ordre. Les
quantificateurs universels servent à modeler le polymorphisme,
tandis que les quantificateurs existentiels modèlent
l'abstraction de données. Ces calculs regroupés sous le
nom de "modèles basés sur des records"
(record-based models) peuvent être résumés
comme une extension du l-calcul typé par des records.
La correspondance entre objets et records est
grossièrement résumée ainsi : les objets
correspondent aux records, les classes aux
générateurs de records, les méthodes aux
champs de records et les messages aux étiquettes
associées aux méthodes. L'envoi d'un message
équivaut à une sélection de champ par son
étiquette dans un record, et l'héritage peut
être vu comme une extension de record. L'exemple
suivant, extrait de [Cast98], illustre bien cette approche, les
records sont représentés par des et les types record par
. Les expressions suivantes
définissent les classes 2DPoint et 2DColorpoint.
Un objet 2Dpoint représente un point avec un état (x,y) définissant ses coordonnées, et disposant de trois méthodes :
- norm qui ramène la norme du vecteur (x,y).
- erase qui ramène le point à l'origine (0,0) et retourne l'objet lui-même.
- move qui translate le point de (dx,dy) et ramène le nouveau point.
La classe 2DColorPoint hérite de la classe 2DPoint. L'état des objets 2DColorPoint est étendu à 'c', qui définit une couleur. La nouvelle méthode isWhite est une méthode supplémentaire propre à la classe 2DColorPoint. Les méthodes norm et erase sont héritées de 2Dpoint. La méthode move, dans le cas d'un 2DColorPoint, en plus de la translation change l'état 'c' en 'white'. Ceci explique que son type est redéfini puisqu'elle agit sur un état spécifique de 2DColorPoint.
Notons que les états x, y, et c (qui correspondent aux variables d'instance dans la terminologie habituelle) ne sont pas explicites dans les définitions données plus hauts. Ils apparaissent comme des paramètres fonctionnels dans les générateurs de records.
Pour créer des instances d'une classe nous avons besoin d'un générateur de records pour la classe.
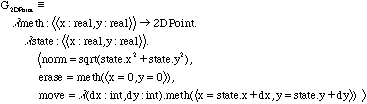
Afin de modéliser les caractéristiques de base d'un langage par objets, il est nécessaire d'inclure le type record, ainsi que des types récursifs et opérateurs de point fixe. L'un des principaux inconvénients de cette approche est le manque de cohérence entre l'héritage et les types récursifs. [Cast98] illustre en détail cette difficulté.
L'approche que nous venons de décrire sommairement a été critiquée par Cardelli et Abadi dans [AbCa95]. Ce dernier article a été le commencement d'une autre façon de formaliser les langages à objets. Bien que le calcul défini dans cet article soit proche du l-calcul, la différence principale tient en ce que les objets primitifs sur lesquels s'effectuent les opérations ne sont pas des abstractions fonctionnelles mais des objets. L'avantage majeur de ce calcul est que l'interprétation des objets se fait d'une façon directe et intuitive. Nous exposons par la suite une brève description de ce calcul.
Cardelli et Abadi proposent une méthodologie en trois étapes : la définition d'un calcul d'objets primitifs, l'élaboration d'un langage à objets et finalement l'élaboration d'un système incluant des classes. La syntaxe du calcul d'objets est minimale, mais sur cette syntaxe on peut exprimer des attributs, des procédures, et des structures de contrôle.
a,b ::= terme.
x variable.
objet.
a.l invocation de méthode.
actualisation de méthode.
clone(a) clonage.
let x=a in b let.
La syntaxe précédente possède en plus des variables, des constructeurs pour la creation d'objets, pour l'invocation de méthodes et pour la réécriture. Les objets sont définis comme une collection de méthodes. En utilisant uniquement ces termes, les auteurs définissent un modèle fonctionnel pour objets à partir duquel on peut interpréter des concepts propres aux langages par objets : classe, héritage, instanciation, etc. Il existe aussi la possibilité d'enrichir ce modèle non typé par divers systèmes de types. Dans ce calcul, il subsiste un inconvénient venant du fait qu'il est fonctionnel : les objets ne maintiennent pas un état propre. C'est pour cela qu'on inclut deux constructeurs additionnels : un pour la déclaration de variables locales (let) et un autre pour la persistance (clone).
Les champs d'un objet s'interprètent comme des méthodes qui n'utilisent pas leur paramètre self. Ainsi, un objet de la classe 2Dpoint avec état x=5 et y=8 est écrit dans ce calcul par :
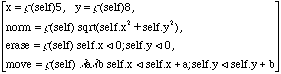
La classe 2Dpoint est un objet de la forme :
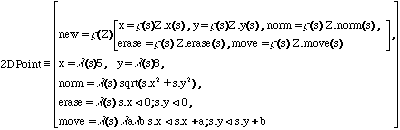
Dans une classe, la méthode new est un générateur d'instances. Les autres champs dans la classe (x, norm, erase, etc.) sont appelés des pré-méthodes. Les pré-méthodes sont des fonctions qui deviennent des méthodes une fois emboîtées dans un objet. Cette stratégie permet la réutilisation des méthodes, nécessaire à la définition d'héritage.
Avant de finir ce bref parcours et d'exposer le calcul que nous avons adopté, nous examinons une dernière approche. La notion fondamentale dans ce dernier type de calculs est la notion de concurrence. Cette notion étrangère aux notions de fonction, contrainte et objet, permet de les reconstruire. En particulier pour les langages par objets : "...la vision de la programmation par objets est concurrente par nature : notre univers est composé d'objets qui interagissent entre eux, souvent les un dépendant des autres..." La première formalisation d'un calcul concurrent a été CCS (Calculus of Communicating Systems) proposée par Milner en 1980 [Miln80]. Le paradigme fonctionnel peut être vu comme un cas particulier du CCS. L'idée qui suivit fut la définition d'un calcul formel comme le l-calcul qui inclurait ce dernier. Ce calcul est le p-calcul. Les notions primitives du p-calcul sont : les processus et les noms. L'interaction entre les processus se fait à travers des canaux de communication identifiés par leur nom. La syntaxe du p-calcul est définie comme suit :
P,Q::= O Processus nul.
Processus préfixe.
Processus concurrent exclusif.
Processus concurrent.
Processus avec nom local.
Processus réplication.
où les préfixes p sont définis par : 
, le premier dénotant
l'opération de lecture dans un canal et le deuxième
celle d'écriture.
En ce qui concerne la programmation par objets, un calcul d'objets concurrent TyCO est défini dans [Vasc94]. De même que dans le calcul d'objets primitifs [AbCa95], les notions d'objet et de message sont des entités primitives du calcul.
Il existe dans TyCO des processus et des agents. Un processus peut prendre les formes suivantes :
Message.
Objet.
Composition concurrente.
Variable locale.
Récriture de variable
d'agent.
Récriture d'Agent.
Instanciation locale.
Agents de la forme 
sont
constitués par un processus P dont les arguments formels sont
.
Agents de la forme recX.A sont appelés agents récursifs, les occurrences de X en A représentant des invocations récursives.
La notion de classe n'est pas une primitive de TyCO, cependant on a la possibilité de définir des classes grâce à la construction :
Class Classname(var1,...,varn) = M
Cette expression n'est qu'une abréviation de l'agent récursif :
rec Classname(self, var1,..., varn)= 
Ainsi pour notre exemple de base, la classe 2DPoint sera définie par :
où
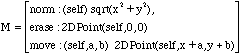
Nous invitons le lecteur intéressé par le sujet à consulter [Miln91] et [Vasc94]. Dans le contexte des langages concurrents, il nous faut citer le langage OZ [Smol95] dans lequel la concurrence est proposée comme élément unificateur des modèles de programmation fonctionnelle, par contraintes et par objets.
Les modèles de calcul que nous avons présentés jusqu'ici, supposent une vision dans laquelle les méthodes font partie de la définition des classes ou des objets. Les langages appartenant à cette famille se situent dans la tradition de Simula [JBKr70]. Des langages plus récents tels que CLOS ou Dylan ont une approche différente et utilisent la notion de multiple dispatch. On parle aussi de fonctions génériques ou fonctions polymorphes. Dans ce cas, la sélection à l'appel d'une fonction se fait dynamiquement sur l'ensemble des types des arguments, vers une méthode définie par ces types ou leurs ascendants. Une différence conceptuelle significative est que l'on considère une fonction, plutôt qu'une classe, comme un ensemble de méthodes. Ce modèle nous semble mieux adapté à nos objectifs parce qu'il rend possible une intégration plus fine des concepts de classe, d'objet et de fonction, et qu'il permet une plus grande dynamicité, dans le sens où rajouter une méthode ne modifie pas la classe. Notons cependant que la notion de classe perd en modularité, ce qui peut avoir des conséquences sur la réutilisabilité.
Les travaux récents de Castagna [Cast98] ont permis de proposer un calcul formel, le l&-calcul, bien adapté aux langages à multiple-dispatching . En utilisant le langage CLOS, nous pouvons aisément nous raccorder à ce formalisme que nous allons détailler ici.
Le l&-calcul est une extension du l-calcul par les records et les fonctions génériques. Une fonction générique n'est qu'une collection de fonctions simples (l-abstractions) appelées méthodes. Pour dénoter les fonctions génériques on utilise le constructeur de collections "&". Ainsi le terme (M&N) dénote une fonction générique Y constituée de méthodes N et M. On doit aussi distinguer l'application simple, dénotée par ".", de l'application pour les fonctions génériques. Pour cela on introduit l'opérateur d'application "·". Ainsi, les fonctions génériques sont notées comme des listes de méthodes construites à l'aide de & et de la liste vide dénotée par e. Une fonction générique à n méthodes est dénotée par :
que nous simplifierons en :
Le type d'une fonction générique constituée
de méthodes 
de type 
, est défini par :
Dans le l&-calcul, tout ensemble de types de méthode
n'est pas un type de fonction générique. Un ensemble de
types de méthodes 
est un type de
fonction générique si et seulement si pour tout i,j
¤ I les deux conditions suivantes sont satisfaites :
est maximal dans 
où LB(U,V) dénote l'ensemble des bornés inférieurs communs aux types U et V.
La relation d'ordre 
est
définie par la liste de priorité de classes LPC (voir
la définition 2.3 plus bas).
L'application d'une fonction générique de type 
à un argument N de type U
consiste en la sélection d'une méthode 
parmi les méthodes de la
fonction générique, suivie de l'application de cette
méthode à N.
Le type U peut ne pas être contenu dans l'ensemble des 
défini par le type de la
fonction générique. Dans ce cas, on sélectionne
la méthode tq. :
Un objets dans le l&-calcul est un record de la forme
, soit un ensemble de champs
étiquetés l=T où l est appelé
l'étiquette et T la valeur. Il existe une règle de
réduction 
pour la
sélection et la réécriture des champs :
Nous ajoutons aussi les règles de contexte :
Si les objets sont vus comme des records, les classes seront alors vues comme des générateurs de records. Nous assumons qu'il existe une fonction générique new et que chaque classe définit une méthode pour cette fonction générique. Nous assumons aussi dans ce qui suit que le type d'un objet est sa classe.
Ainsi, le mécanisme d'héritage dans le l&-calcul
est défini par le sous-typage associé aux
records (la relation 
à un objet appartenant
à la classe C, alors la méthode 
sera exécutée. Si 
= C, alors l'objet utilise la méthode
définie par sa classe C, par contre si 
, alors l'objet utilise une méthode
héritée de 
. Les
difficultés introduites par l'héritage multiple seront
heuristiquement résolues ; l'algorithme sera
présenté ultérieurement.
Le l&-calcul va un peu à l'encontre de l'approche traditionnelle selon laquelle les messages sont passés aux objets. Ici, ce sont plutôt les objets qui sont passés aux messages (les fonctions génériques). Un des grands avantages de ce modèle est la possibilité d'utiliser le multiple dispatch, c'est-à-dire la capacité de sélectionner une méthode en prenant en compte d'autres arguments que le premier argument de la fonction. Une autre caractéristique importante du l&-calcul est qu'il permet d'ajouter des méthodes à une classe existante sans modifier le type des instances de la classe. Un dernier avantage de ce modèle est que les fonctions génériques sont des citoyens de premier ordre, par exemple nous pouvons écrire le terme suivant :
Nous reprenons notre exemple habituel que nous réécrivons dans le formalisme du l&-calcul :
Les objets s'expriment sous la forme de records des champs.
Il existe un ensemble de fonctions génériques qui définissent les méthodes pour les classes.
)
La fonction générique new contient une méthode qui permet de générer des instances 2DPoint.
où 2DPointClass est une méta-classe dont la classe 2Dpoint est une instance.
Des travaux futurs dans le l&-calcul sont envisageables, particulièrement la définition de langages à multiple dispatch typés, et aussi pour l'élaboration de techniques d'inférence de types pour les langages existants.
2.1.2 Modèles de langages visuels.
En ce qui concerne la spécification du langage visuel, nous allons suivre la méthodologie utilisée dans la section précédente : faire un résumé de quelques travaux représentatifs, afin d'en mettre en évidence les difficultés principales, pour exposer ensuite notre proposition.
Dans [MaMe96b] nous trouvons une classification des formalismes de spécification de langages visuels suivant les trois approches algébrique, logique et grammaticale. Nous exposons un bref résumé de chaque approche.
- Langages à Icônes basés sur une approche algébrique.
Dans cette approche, un langage visuel est une représentation d'entités et d'opérations à l'aide d'arrangements d'icônes que nous appelons "phrases visuelles". De même que pour le langage naturel, un langage à base d'icônes est fondé sur un vocabulaire composé d'icônes primitifs.
Un icône primitif X est une paire (Xm, Xi) où Xm est appelé le signifiant de l'icône ou partie logique et Xi est appelé l'image de l'icône ou partie physique. Les deux parties d'un icône sont mutuellement dépendantes. L'image d'un icône doit contenir des caractéristiques globales qui représentent le concept principal de l'icône, ainsi que des caractéristiques locales qui expriment un concept secondaire. Le signifiant d'un icône est généralement une structure conceptuelle.
En plus des primitives, on définit un ensemble d'opérateurs entre icônes qui nous permettent de construire de nouveaux icônes. L'exemple suivant montre la construction d'un nouvel icône à l'aide de l'opérateur d'interprétation contextuel (CON).
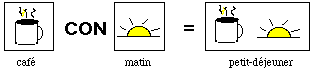
Figure 2-1 Construction d'un icône à partir de deux icônes primitifs.
La conception d'un langage visuel selon cette perspective peut être énoncé comme suit. Soit K un ensemble de mots (par exemple, un sous-ensemble du langage naturel ou un ensemble de commandes pour une application) ; alors la conception du langage iconique associé à K doit suivre les trois étapes suivantes :
- Définition des mots primitifs en K.
- Création d'un icône pour chaque primitive.
- Codage de tous les mots de K sous la forme de phrases construites à l'aide de primitives et des opérateurs.
Bien que la méthodologie soit en théorie bien définie, nous nous interrogeons sur la difficulté de la mise en Ïuvre de chaque étape. Un exemple complet de cette approche peut être trouvé dans [CPOT97].
- Une approche logique : raisonnement spatial.
La sémantique et la syntaxe d'un langage visuel sont définies ici en utilisant des relations topologiques entre diverses primitives. Prenons par exemple les définitions suivantes :
- Primitives lexicales
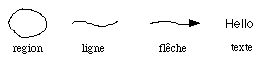
- Relations spatiales
Nous pouvons définir la syntaxe de l'élément terme du langage, comme une spécification spatiale en utilisant les relations définies entre les primitives lexicales.
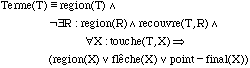
Comme pour l'exemple précédent, une description de chaque composant du langage est faite en utilisant une logique descriptive. Ce choix obéit en grande partie à la grande quantité de travaux et de résultats dans le domaine de la vérification pour les logiques de descriptions [Napo98]. Le langage Pictorial Janus [KSHa91] est défini de cette façon [Haar95]. Parmi les avantages de cette approche, on souligne que l'écriture d'un programme est indépendante de l'éditeur, car les spécifications sont d'ordre topologique. Ainsi, chaque état pendant l'exécution d'un programme peut être visualisé.
- Une approche grammaticale.
Les Constraint Multiset Grammars (CMG) sont des systèmes de réécriture pour multi-ensembles d'objets typés. Un CMG est défini par :
Où 
dénote
les symboles terminaux et 
les symboles
non terminaux, avec
.
Le symbole TS est appelé le symbole initial,
. P est un ensemble de productions.
Une production X suit la syntaxe suivante :
where exists 
where 
and 
La production précédente nous dit que le non
terminal X peut être réécrit comme un
multi-ensemble 
s'il existe un
contexte 
tel que la
contrainte C, définie sur les attributs de chaque 
et 
, est
satisfaite. De plus, les valeurs des attributs de X
dénotés par 
sont
définies par le vecteur E composé de valeurs d'
attributs des et des 
.Les éléments du
contexte 
ne sont pas
réduits lors de l'application d'une production, leur existence
est seulement vérifiée. Voici un exemple :
TR:transition ::= F:fleche , T:texte where exist R:etat , S:etat
where T.centre touche F.centre
S.rayon = (distance (F.fin , S.centre))
R.rayon = (distance (F.debut , R.centre))
and
TR.de = R.nom
TR.vers = S.nom
TR.label = T.string
D'une façon générale, le langage L est défini par :
où :
est une dérivation.
Nous remarquons certaines constantes dans les trois approches étudiées. La plus importante semble être la difficulté de définir les frontières entre lexique et syntaxe. Le choix de primitives lexicales peut donc obéir à différents facteurs, entre autres à la fréquence d'utilisation, au degré de formalisation, etc. Après avoir choisi les primitives, il faut aussi faire des choix sur leur structure ; peuvent-elles avoir des attributs ? Si les primitives possèdent des sous-objets ou des attributs, quel type de calcul est permis entre les attributs ? On doit aussi décider de l'interprétation des relations spatiales entre objets et, plus encore, de la structure mathématique sous-tendant les expressions visuelles.
Nous décrivons dans la section suivante notre langage, OpenMusic, dont les spécifications visuelles suivent une approche grammaticale.
2.2.1 Le langage visuel d'OpenMusic.
2.2.1.1 Spécification lexicale.
Les choix des primitives lexicales dans notre spécification nécessite un certain nombre de décisions. Il nous semble qu'une description lexicale de très bas niveau rendrait notre description plus formelle mais aussi plus complexe. Nous avons choisi de faire abstraction de la formalisation de certains objets de base et d'assumer leur définition de manière axiomatique. Ainsi nous supposons l'existence d'un ensemble d'éléments graphiques de base : l'icône, le rectangle, la ligne et le texte. En général, de telles formes ne se rencontrent pas de manière isolée mais sont plutôt combinées pour former des éléments de plus haut niveau que nous appelons primitives lexicales.
Nous supposons, sans entrer dans les détails, que nous disposons de deux types de relations spatiales de base : Contenant et En contact. Ainsi, de la même façon qu'il est possible de définir un rectangle comme une relation entre lignes, nous allons définir un certain nombre de constructions à partir des éléments graphiques de base et des deux relations mentionnées. Ainsi les primitives lexicales sont :
Un cadre de texte est défini par un rectangle contenant un texte, la figure suivante est un exemple général de cadre de texte :
Un Cadre simple est composé d'un icône en contact avec un texte :
Les exemples de cadres simples de la figure précédente nous permettent de déduire que la position du texte par rapport à l'icône n'est pas imposée. Cependant nous rencontrerons les cadres simples essentiellement sous les deux formes présentées.
Un cadre composé est constitué d'un rectangle contenant un ensemble de cadres simples, de cadres de texte et éventuellement un ensemble des lignes.
On définit le cardinal d'un cadre composé F, Card(F), par le nombre de cadres simples ou de cadre de texte qu'il contient.
Il existe trois types différents de lignes dans OpenMusic : ligne simple, flèche, ligne pointillée.
Une séquence est une forme particulière de cadre composé qui exprime une relation d'ordre entre les cadres simples qui lui appartiennent. Cette relation est représentée par la coordonnée des positions des cadres simples suivant un des axes du rectangle qui constitue la séquence.
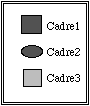
Les séquences se différencient des cadres composés par le fait que le rectangle est construit avec une double ligne. Dans la figure précédente la relation d'ordre est donnée par :
Cadre1 < Cadre2 < Cadre3.
Ainsi un programme en OpenMusic s'exprime comme un agencement sur l'écran de cadres composés vides ou non. Par mesure de simplicité, les cadres de texte seront désormais assimilés aux cadres simples.
OpenMusic est un langage basé sur des noms. Nous définissons donc l'ensemble N des noms du langage par :
N = Nc È Ni È Nf È Np È Ng
Où Nc , Ni , Nf , Np , Ng sont eux-mêmes des ensembles appelés respectivement, noms de classe, noms d'instance, noms de fonction, noms de patch et noms généraux. L'intersection de ces ensembles est vide deux à deux.
De la même manière, nous définissons l'ensemble I des icônes par :
I = Ic ª If ª {Pi} ª {Po} ª {Ip} ª {Ao} ª {Ai}
Où Ic, If sont appelés respectivement : icônes de classe et icônes de fonction,
On défini l'ensemble Ib dénommé icônes de boîtes par :
Ib = Ic ª If ª {Ip}
En d'autres termes, ceci signifie que l'ensemble icône de boîte est soit un icône de classe, soit un icône de fonction, soit l'icône de patch.
Nous distinguons parmi l'ensemble de cadres simples les ensembles Fc, Fi, Fs, Ff et Fb constitués comme suit :
- Cadre simple de classe Fc
- Cadre simple d'instance Fi
- Cadre simple de champ Fs
- Cadre simple de fonction Ff
- Cadre simple de boîte Fb
Nous avons constaté la difficulté de définir précisément la frontière entre lexique et syntaxe ; par exemple les objets cadres composés sont des objets éditables, et pourtant nous les avons considérés comme des primitives lexicales. Nous avons choisi de réserver le statut syntaxique aux objets de base du langage de programmation (classes, instances, méthodes, etc.).
2.2.1.2 Spécification syntaxique.
Nous décrirons ensuite comment les entités de notre langage sont représentées graphiquement à l'aide des termes visuels définis précédemment. Les entités sont les concepts abstraits de programmation qui sont sous-jacents au langage visuel. Elles sont constituées de termes tels que classe, instance, champ, fonction, etc. que nous ne définirons pas et qui sont à considérer dans leur acception habituelle. Chacune de ces entités peut être représentée de manière élémentaire et compacte sous la forme d'une vue ou de manière plus développée et éditable sous la forme d'un container. Les vues d'une entité sont construites à l'aide de cadres simples et de lignes. Les containers sont des cadres composés, auxquels on adjoindra des cadres de textes en contact avec le bord supérieur. Les textes correspondants seront éventuellement vides, auquel cas on ne dessinera pas le cadre de texte. Plusieurs vues mais un seul container d'une même entité peuvent coexister visuellement à un moment donné.
Avant de définir les représentations visuelles des entités, nous avons besoin d'introduire un certain nombre de constructions syntaxiques intermédiaires : les relations de prise d'entrée (on utilisera le terme inlet), les relations de prise de sortie (outlet), les relations de passage d'argument (connexions ) et les relations d'héritage.
On évoquera par la suite un inlet comme un triplé (source, cible, indice).
On évoquera par la suite un outlet comme un triplé (source, cible, indice).
On évoquera par la suite une connexion comme un couple (source, cible).
Nous donnons maintenant la description syntaxique des entités sous les formes de vues et de containers :
- Il existe une vue unique v pour les champs.
où v est un cadre simple de champ.
- Le container d'un champ contient un cadre simple de champ et un cadre de texte appelé valeur par défaut.
Pour le cadre de texte en contact avec le cadre composé, classname aparttient à Nc.
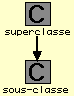
- Les vues d'une classe peuvent être : un cadre simple de classe ou bien un cadre de texte où classname aparttient à Nc.
- Le container d'une classe est une séquence contenant uniquement des vues de champs. classname aparttient à Nc.
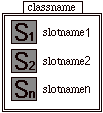
-Une instance a deux types possibles de vues, soit un cadre simple d'instance ou un cadre de texte avec instname aparttient à Ni.
- Un container d'instance est une séquence contenant des vues d'instance.
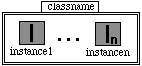
classname e Nc.
Un cas particulier d'instance concerne les listes, dont la représentation sous forme de vue et de container est donnée dans la figure suivante :
- La vue d'un paramètre d'entrée est un cadre simple dont l'icône est Pi et le texte est un nom e Ng. Par commodité, on n'affichera pas ce nom, la différence de position spatiale indiquant clairement la différence entre plusieurs paramètres d'entrée.
- Le container d'un paramètre d'entrée est un cadre composé contenant un unique élément à l'intérieur de type cadre de texte.
- La vue d'un paramètre de sortie est un cadre simple dont l'icône est Po et le texte est un nom aparttient à Ng. Par commodité, on n'affichera pas ce nom, la différence de position spatiale indiquant clairement la différence entre plusieurs paramètres de sortie.
- Il n'existe pas de container pour un paramètre de sortie.
- La vue d'un représentant de classe est définie par un triplé (f, indice, R)
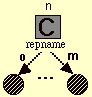
Où
f est un cadre simple de boîte, avec icône (f) aparttient à Ic
l'indice n est un texte en contact avec la partie supérieure de f,
R est un ensemble fini non vide d'outlets {(s0,c0,i0),...,(sm,cm,im)} satisfaisant :
si = f
ci ¹ cj ii ¹ ij
max{i0,...,im} = m
pour 0 £ i,j£ m i¹ j.
On doit satisfaire aussi card(R) = Card(Cont) + 1 où Cont est le container de la classe représentée. Le nombre d'oulets est donc égal au nombre de champs de la classe + 1.
Par la suite, pour simplifier, les vues de représentants de classe seront remplacées par :
Où chaque outlet est remplacé par Po qui est en contact avec la partie inférieure de f. Les étiquettes de valeur entière, numérotées de façon croissante à partir de 0, permettent de déterminer la position des icônes Po de gauche à droite.
- Le container d'un représentant de classe est un cadre composé contenant deux cadres simples appelés valeur et indice : valeur est une vue d'instance et indice est un cadre de texte.
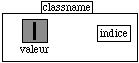
classname aparttient àNc.
- La vue d'une boîte est composée par (f ,R ,R')
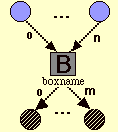
Où
f est un cadre simple de boîte, f aparttient à Fb
R est un ensemble d'inlets {(s0,c0,i0),...,(sn,cn,in)} satisfaisant :
ci = f
si ¹ sj ii ¹ ij
max{i0,...,in} = n
pour 0 £ i,j£ n i¹ j.
R' est un ensemble d'outlets {(s'0,c'0,i'0),...,(s'm,c'm,i'm)} satisfaisant :
s'i = f c'i ¹ c'j
i'i ¹ i'j
max{i'0,...,i'm} = m
pour 0 £ i',j'£ m i'¹ j'.
Par la suite, les vues de boîtes seront simplifiées par :
Où :
- Chaque outlet est remplacé par Po alors en contact avec la partie inférieure de f.
- Les étiquettes dans R', numérotées de façon croissante à partir de 0, permettent de déterminer la position des icônes Po de gauche à droite.
- Chaque inlet est remplacé par Pi alors en contact avec la partie supérieure de f.
- Les étiquettes dans R, numérotées de façon croissante à partir de 0, permettent de déterminer la position des icônes Pi de gauche à droite.
Dans le même esprit de simplification, nous identifierons terminologiquement les inlets et les outlets avec les paramètres d'entrée et de sortie.
Une boîte peut éventuellement "contenir" une étiquette (cadre de texte) qu'on appellera visualisateur d'état.
Une boîte avec visualisateur d'état X est appelée une boîte verrouillée (dans le même sens que dans 1.3.1.1.).
- Le container d'une boîte est un cadre composé de trois cadres simples nommés référence, valeur et état.
Valeur est une liste. Référence peut être une vue de classe, une vue de patch ou une vue de fonction générique. Selon le cas, les boîtes seront alors appelées respectivement factory, invocation de patch ou invocation de fonction générique.
Dans le cas d'une factory la boîte doit satisfaire en plus :
card (R) = card (Cont ) + 1
card (R') = card (Cont) + 1
où Cont est le container associé à référence. On rappelle que référence est dans ce cas une vue de classe, et que le container associé contient l'ensemble des champs de la classe. Une factory a donc un nombre d'inlets et d'outlets égal au nombre des champs de la classe référence + 1.
- La vue d'un objet absout est constituée par un triplet (f , r , i)
où
f est un cadre simple avec icône(f) = Ao et name(f) aparttient à Ng.
i est un texte "superposé" à Ao appelé indice.
r est un inlet (S , C , I) avec C = f et I =0.
La vue d'un objet absout sera simplifiée par :
- Il n'existe pas de container pour les objets absout.
La vue d'un objet absin est constituée par un triplet (f , r , i)
avec
f un cadre simple avec icône(f) = Ai ; name(f) aparttient à Ng.
i un texte "superposé" à Ai appelé indice.
r un outlet (S , C , I) avec S = f et I =0
Dans la suite, la vue d'un objet absin sera simplifiée par :
- Le container d'un objet absin est un cadre composé contenant deux cadres simples, appelés valeur et indice.
Valeur est une vue d'instance et indice un cadre de texte.
- Les vues des objets méthode se définissent par un couple (f , LE)
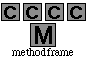
où f est un cadre simple ; f aparttient à Ff et LE une liste de spécialisateurs en contact avec le bord supérieur de f.
Une liste de spécialisateurs est une liste dans laquelle chaque élément est une vue iconique de classe.
Pour simplifier, nous montrerons une liste de spécialisateurs sous la forme :
Tout en gardant en tête la propriété d'ordre des séquences.
- Le container d'une méthode est un cadre composé incluant B, RC, C et O
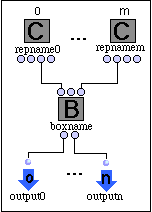
où
B est un ensemble de boîtes,
RC est un ensemble de représentants de classe
O est un ensemble d'absouts
C est un ensemble de connexions {(s0,c0),...,(sk,ck)}
satisfaisant :
O
RC
Card(RC) = Card(LE) = m+1
clôture(b)
Cette dernière propriété est particulièrement importante puisqu'elle prévient de la formation de cycles dans le graphe de connexions. Pour définir la clôture d'une boîte, nous définissons l'ensemble connected pour une boîte b par :
La clôture de b est définie par :
clôture(b) = connected (b) È 
clôture(bi)
D'autre part, il existe une correspondance bijective entre les représentants de classe de l'ensemble RC et les spécialisateurs apparaissant dans la vue de méthode. Les représentants et les spécialisateurs appariés réfèrent aux mêmes classes. L'indice croissant des représentants correspond à l'ordre de gauche à droite des spécialisateurs.
Nous simplifierons la représentation d'un container de méthode en :
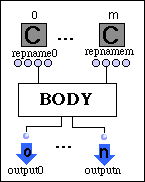
- La vue d'une fonction générique est un cadre simple de fonction.
- Le container d'une fonction générique est un cadre composé contenant des vues de méthodes ; genfunframe aparttient à Nf.
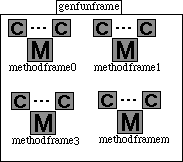
De plus, on doit vérifier pour toute méthode (f,LE) que :
- La vue d'un patch est un cadre simple f.
Avec icône(f) = Ip et name(f) aparttient à Np
- Le container d'un patch est un cadre composé incluant B, I, C et O
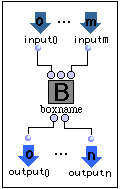
où
B est un ensemble de boîtes,
A est un ensemble d'absin,
O est un ensemble d'absouts,
C est un ensemble de connexions.
satisfaisant :
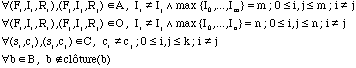
Nous simplifierons la représentation d'un container de patch en :
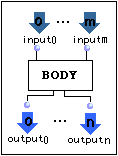
2.2.1.3 Sémantique opérationnelle.
Le patch est un objet central dans OpenMusic. Dans sa forme développée (container de patch) il constitue pour le langage visuel une expression correspondant à la notion commune de corps de programme. A l'intérieur d'un patch, il y a des boîtes et des connexions qui représentent un graphe d'invocations fonctionnelles. On peut demander l'évaluation en n'importe quel point de ce graphe (sur n'importe quelle boîte). L'évaluation d'une boîte est déclenchée lors de l'évaluation d'une de ses sorties (outlets). Il y a ainsi une chaîne d'évaluations qui correspond à l'exécution du programme.
Nous allons donc interpréter les éléments décrits jusqu'ici en termes d'évaluation. La relation d'équivalence définie dans les règles suivantes inclut que pour un objet les vues multiples d'une même entité sont équivalentes entre elles ; elles sont aussi équivalentes aux containers de la même entité. L'évaluation d'un patch à n entrées (absin) demande l'association de chaque argument passé au patch avec la partie valeur de l'absin correspondant. Cette assignation n'est valable que dans le contexte défini pour l'évaluation du patch.
La sémantique est donnée sous la forme d'un ensemble de règles de réductions qui transforment les expressions graphiques en expressions Lisp. Ces règles utilisent un petit nombre de primitives Lisp telles que first, rest, member, et funcall. De même, elles supposent l'identification des séquences aux listes Lisp. D'autres langages cibles peuvent être choisis à condition de fournir ces primitives.
- Règles d'évaluation.
(R1) Cadre de texte.
L'évaluation d'un cadre de texte se réécrit en le texte contenu dans le rectangle.
(R2) Instances.
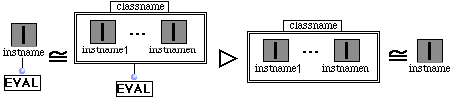
L'évaluation d'une instance se réécrit en l'instance elle-même.
(R3) Paramètre d'entrée.
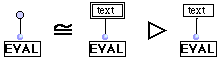
Si le paramètre d'entrée ne fait pas partie d'une connexion, l'évaluation d'un paramètre d'entrée se réécrit en l'évaluation du cadre de texte contenu dans son container.
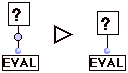
Si le paramètre d'entrée fait partie d'une connexion (source,cible), l'évaluation d'un paramètre d'entrée se réécrit en l'évaluation de source.
(R4) AbsIn.
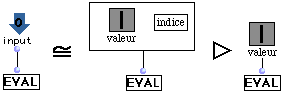
L'évaluation d'une AbsIn se réécrit en l'évaluation de l'instance "valeur" dans son container.
(R5) AbsOut.
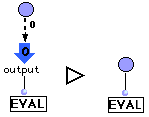
L'évaluation d'une AbsOut se réécrit en l'évaluation de son inlet.
(R6) Boîte verrouillée.
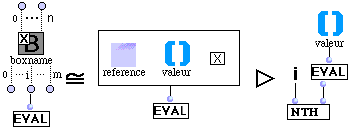
L'évaluation d'une boîte verrouillée par son ième outlet se réécrit en le ième élément de l'évaluation de la liste "valeur" du container de la boîte.
(R7) Boîte Invocation de fonction.
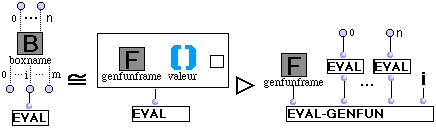
L'évaluation d'une boîte Invocation de fonction par son ième outlet se réécrit en un appel à Eval-Genfun (R12) avec les paramètres : la référence de la boîte, l'évaluation du premier inlet de la boîte,..., l'évaluation du nème inlet de la boîte et l'indice de l'outlet évalué).
(R8) Boîte Invocation de patch.
L'évaluation d'une boîte Invocation de patch par son ième outlet se réécrit en un appel à Eval-Patch (R11) avec les paramètres : la référence de la boîte, l'évaluation du premier inlet de la boîte,..., l'évaluation du nème inlet de la boîte et l'indice de l'outlet évalué).
(R9) Boîte Factory.
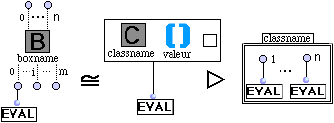
L'évaluation d'une boîte Factory par son premier outlet se réécrit en une instance de la classe qui est la référence de la boîte.
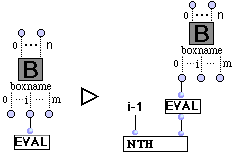
L'évaluation d'une boîte Factory par son ième outlet (i¹ 0) se réécrit en le i-1ème élément de l'évaluation de la factory par son premier outlet.
(R10) Représentant de classe.
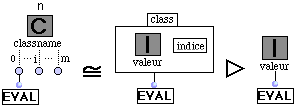
L'évaluation d'un représentant de classe par son premier outlet se réécrit en l'évaluation de l'instance "valeur" dans son container.
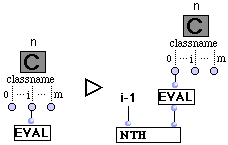
L'évaluation d'un représentant de classe par son ième outlet (i¹ 0) se réécrit en le i-1ème élément de l'évaluation du représentant de classe par son premier outlet.
(R11) Patch.
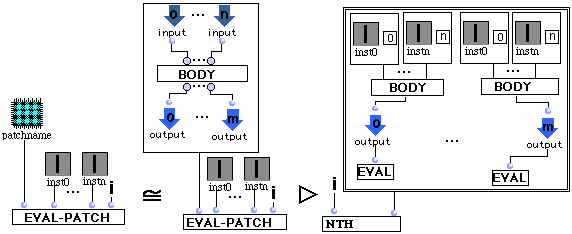
Eval-patch d'un patch avec arguments inst0,...,instn et i se réécrit en le ième élément d'une liste dont l'élément k est le résultat de l'évaluation du kéme absout du container du patch. L'instance "valeur" du container de chaque jème absin du patch est remplacée par instj.
(R12) Fonction générique.
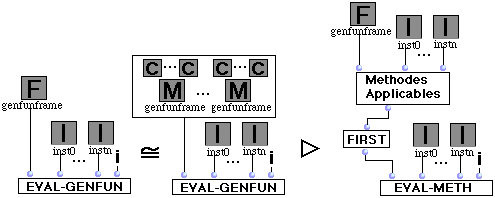
Eval-Genfun d'une fonction générique avec arguments inst0,...,instn et i se réécrit en un appel à Eval-Meth (R13) avec les paramètres : la première méthode de la liste de méthodes applicables, inst0,...,instn et i. La liste des méthodes applicables d'une fonction générique pour une liste d'arguments ?1,...?n est une liste ordonnée par la relation <M où chaque méthode satisfait les arguments (voir annexe II.1 pour la description en détail de ces règles).
(R13) Méthode.
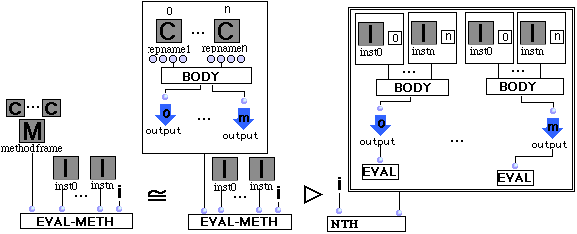
Eval-meth d'une méthode avec arguments inst0,...,instn et i se réécrit en le ième élément d'une liste dont l'élément k est le résultat de l'évaluation du kéme absout du container de la méthode. L'instance "valeur" du container de chaque jème absin de la méthode est remplacée par instj.
2.2.1.3.2 Arbres d'héritage et liste de priorité de classes.
L'arbre d'héritage est un graphe dirigé sans cycles et consistant (la définition de consistance sera donnée dans la définition 2.4). L'ordre d'héritage (la liste de priorités de classes) décrit ici est tiré de [Steel98] et est utilisé dans CLOS.
Terminologie
Pour la figure précédente on dira que :
- La classe note est une sous-classe directe de la classe score-ele.
- La classe note est une sous-classe de la classe element.
- La classe score-ele est une super-classe directe de la classe note.
- La classe element est une super-classe de la classe note.
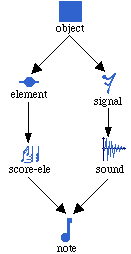
Figure 2-2 Exemple d'un arbre de hiérarchie de classes.
Définition 2.1 ( liste de précédence d'une classe )
On définit Rc la liste de précédence d'une classe C par :
Rc = 
où 
sont les
super-classes directes de C ordonnées de gauche à
droite.
Définition 2.2
Soit une classe C et soit Sc l'ensemble contenant C et toutes ses super-classes, nous définissons la relation R ainsi :
Définition 2.3 (liste de priorité de classes)
La liste de priorité de classes LPCc d'une classe C est un ordre topologique de Sc par rapport a R défini par l'algorithme suivant :
0- S'il existe une séquence 
avec aparttient
à
Sc tq. 
précède 
et 
précède 
en
R
retour R est inconsistant.
1- Mettre C dans LPCc et enlever C de Sc ainsi que toutes les paires (C,D) de R avec D aparttient à Sc
2- Trouver une classe K dans Sc telle qu'aucune classe ne précède K en R
Si une telle classe n'existe pas allez à 5.
S'il existe plusieurs candidats, sélectionner la classe qui a la sous-classe directe la plus à droite dans la LPCc calculée jusque-là.
3- Mettre K dans LPCc et enlever K de Sc ainsi que toutes les paires (K,D) de R avec D aparttient à Sc
4- Aller à 2.
5- Si Sc ¹ {} retour R est inconsistant.
Sinon retour LPCc
Définition 2.4 (consistance d'un arbre héritage)
Un arbre héritage est consistant si pour toute classe appartenant à l'arbre, la relation R de la classe est consistante.
L'exemple suivant détermine la LPC de la classe note dans la Figure 2-2.
Snote={note, score-ele, sound, element, signal, object}
R = {(note , score-ele) (score-ele , sound) (score-ele , element) (sound , signal)
(element , object) (signal , object)}
LPC = {note}
Snote = {score-ele , sound , element , signal , object}
R = {(score-ele , sound) (score-ele , element) (sound , signal)
(element , object) (signal , object)}
candidats possibles (K)= score-ele
candidat = score-ele
LPC = {note , score-ele}
Snote = {sound , element , signal , object}
R = {(sound , signal) (élément , object) (signal , object)}
candidats possibles = sound et élément
candidat = element (car score-ele est une sous-classe d'element)
LPC = {note , score-ele , element }
Snote = {sound , signal, object}
R = {(sound , signal) (signal , object)}
candidats possibles = sound
candidat = sound
LPC = {note , score-ele , element , sound}
Snote = {signal , object}
R = {(signal , object)}
candidats possibles = signal
candidat = signal
LPC = {note , score-ele , element , sound, signal}
Snote = {object}
R = {}
candidats possibles = object
candidat = object
LPC = {note , score-ele , element , sound, signal , object}
Snote = {}
R = {}
LPC = {note , score-ele , element , sound, signal , object}
Après avoir défini la liste de priorité de classe pour un classe donnée, nous énonçons le prédicat suivant, indispensable pour la sélection d'une méthode (voir Annexe II.1).
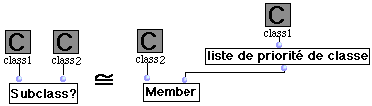
2.2.1.4 Approche fonctionnelle d'OpenMusic.
La sémantique opérationnelle jusqu'ici donnée n'est pas complète, dans le sens où il existe des opérateurs tels que nth, member et first n'étant pas définis dans notre langage. L'arithmétique ainsi que les diverses opérations concernant des types primitifs, principalement les listes, sont déléguées au langage Lisp. Nous définissons un nouvel élément de notre langage appelé Fonction Lisp, ayant pour vue :
En réalité, les fonctions Lisp ne sont pas éloignées des patchs. La principale différence consiste en la non existence d'une visualisation sous la forme de container, donc en l'impossibilité d'édition graphique. Nous introduisons aussi un nouveau type de boîte appelée Invocation de Fonction Lisp, ayant comme référence une Fonction Lisp.
- Vue
- Container
La règle d'évaluation d'une boîte d'invocation de fonction Lisp verrouillée, reste la même que pour une boîte traditionnelle. Ainsi, la seule règle à définir est :
(R14) Boîte d'invocation de fonction Lisp.
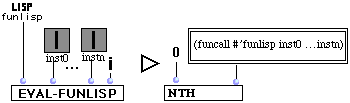
Quelques remarques sont nécessaires pour cette règle :
- Les fonctions lisp ont une sortie unique, donc le résultat sera toujours le premier élément d'une séquence ayant pour unique élément l'instance, produit de l'invocation de la fonction Lisp. Nous gardons cette option par cohérence avec les autres boîtes.
- La liste résultat dans la partie droite de la règle (R14) est incohérente avec la définition de liste donnée dans 2.2.1.1. En effet, nous avons forcé les éléments d'une séquence à être des cadres simples et non des expressions Lisp. Si nous voulons retarder l'inévitable traduction en Common Lisp, nous sommes obligés d'introduire les divers types de base du langage Lisp tels que entiers, chaînes de caractères, listes, etc. Nous définissons un ensemble de Classes Lisp par :
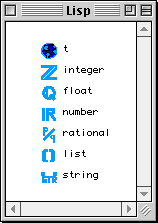
Les Classes Lisp ne peuvent pas être sous-classées, toutefois on peut construire des méthodes spécialisées par ces classes. Nous n'avons prédéfini qu'une petite partie des types disponibles dans Common Lisp, cependant il existe un protocole simple permettant de rajouter de nouvelles classes (e.g. la classe vector). Ce protocole est défini par les méthodes get-icon-id et get-default-value. Parmi les Classes Lisp nous distinguons la classe universelle t. Toutes les classes dans le graphe des types, héritent de la classe t [Habe96].
L'intégration du langage Lisp permet non seulement la définition des éléments et des opérateurs de bas niveau, mais offre aussi la possibilité d'intégrer et de visualiser de façon transparente tout code écrit en Lisp.
2.2.1.5 Approche objet d'OpenMusic.
Dans OpenMusic, toute instance appartient à une classe. La principale différence avec les langages par objets traditionnels, où les classes sont définies par leurs champs et leurs méthodes, réside dans le fait que dans OpenMusic les méthodes appartiennent à une fonction générique, qui se substitue à la notion de message. Cette différence est plutôt d'ordre syntaxique si l'on omet la modularité qui n'est pas la même dans les deux systèmes. Ainsi, la définition d'une classe consiste, d'abord, en la définition des champs déterminant la structure de la classe. La définition des méthodes, elle, est séparée de la définition de la classe et se fera lors de la définition d'une fonction générique. L'utilisateur peut, à l'aide du mécanisme de glisser-déposer définir une classe en ajoutant des vues de champs dans un container de classe.
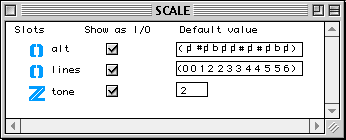
Figure 2-3 Définition d'une classe en OpenMusic.
L'exemple précédent définit la classe scale contenant trois champs :
- alt de type list pour spécifier les symboles d'altérations pour chaque note dans l'échelle.
- lines de type list pour spécifier la position dans la portée de chaque note.
- tone de type integer spécifiant si l'échelle est en demi, quart ou huitième de ton.
Tous les champs dans cette classe sont publics, ce qui est visualisé dans la colonne Show as I/O. La notion de public employée ici, renvoie à la manière dont une classe est utilisée dans un patch. Lorsqu'on glisse un icône de classe sur un éditeur de patch, on dépose en réalité une factory sur ce patch. Une factory est un générateur d'instances. Tous les champs publics de la classe associée sont disponibles en entrée et en sortie (sous la forme d'inlets et d'outlets) de la factory, ce qui permet d'initialiser les champs à la création d'une nouvelle instance, et de lire leur valeur en sortie. Si un champ n'est pas déclaré public, il n'aura pas d'inlet ni d'outlet et ne sera donc pas visible, du moins au niveau de l'interface de création d'instance.
L'utilisateur a la possibilité de définir des nouvelles classes ou de redéfinir des classes déjà existantes, soit par addition ou suppression de champs, soit en changeant les propriétés d'un champ donné (i.e. nom, type, valeur par défaut, etc.). L'interface est extrêmement simple puisqu'il suffit d'ouvrit le container d'une classe ou de créer une nouvelle classe avec son container associé, puis de demander la création de nouveaux champs. Le typage des champs est accompli en glissant l'icône d'une classe existante et en le déposant sur le champ considéré.
Comment spécifie-t-on la structure d'héritage ? Dans l'exemple suivant nous allons créer une nouvelle classe appelée virchord qui hérite de la classe prédéfinie chord.
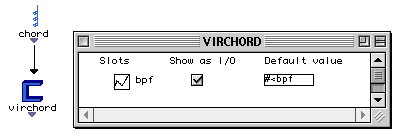
Figure 2-4 Exemple d'héritage.
Chord est une classe standard d'OpenMusic qui représente un accord. D'abord nous demandons la création d'une nouvelle classe virchord. La vue iconique de classe est créée automatiquement ainsi que ses containers associés. Nous relions ensuite par une flèche l'icône virchord à l'icône chord. Dans le container de virchord, nous ajoutons un champ appelé bpf. Nous glissons sur ce champ l'icône de la classe bpf (une classe standard qui définit une fonction linéaire par segment).
Nous aimerions que lors de l'initialisation d'une instance de virchord, le champ bpf soit rempli avec une nouvelle instance de la classe bpf (cette instance contenant une courbe dont les ordonnées sont les valeurs Midi des notes de l'accord). Nous aimerions d'autre part qu'en plus des notes spécifiées par l'utilisateur en entrée de la factory chord, le mécanisme d'initialisation rajoute une note grave, appelée fondamentale virtuelle, à la liste des notes. Pour cela, l'utilisateur a la possibilité de définir la méthode d'initialisation d'instance propre à la classe virchord.
Dans la Figure 2-5, on voit le container (l'éditeur) de la méthode d'initialisation de la classe virchord. Dans la partie supérieure, on peut voir une série horizontale d'icônes de représentants de classes. Ces icônes représentent les paramètres d'entrée de la méthode. Ils correspondent exactement aux inlets qui apparaissent sur l'icône de la factory virchord et, sauf le premier à gauche (self), aux champs de la classe virchord. Self représente l'instance elle même. lmidic, lvel, loffset, ldur, lchan sont les champs hérités de la super-classe chord . Ces champs ont un type simple et possèdent donc un seul outlet. bpf est l'unique champ direct de la classe virchord. La classe bpf possède deux champs (une liste d'abscisses et une liste d'ordonnées). Le représentant de classe pour bpf a donc trois outlets, un pour l'instance bpf elle même et deux pour ses champs.
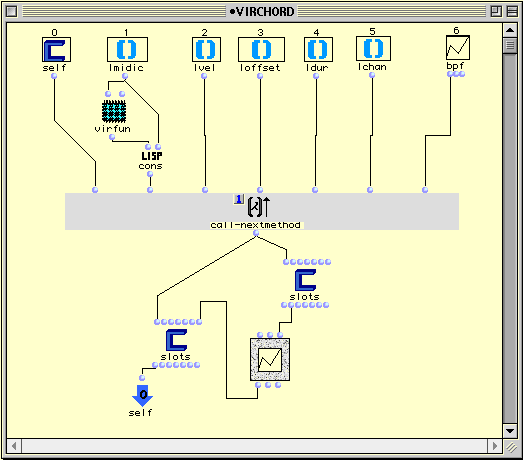
Figure 2-5 Définition d'une méthode d'initialisation d'instance.
La boîte call-next-method est une construction standard de Common Lisp qui invoque la méthode correspondante spécialisée sur la première super-classe de la LPC (ici, la classe chord). Nous constatons donc que l'initialisation habituelle d'un chord en fonction des paramètres d'entrée sera effectuée, à ceci près que nous effectuons un pré-traitement sur le paramètre lmidic. Nous calculons une nouvelle note (la fondamentale virtuelle) grâce à l'invocation du patch virfun (voir annexe II 3) et nous rajoutons cette note en tête de la liste de notes passée en paramètre. Nous pouvons considérer cette première étape de calcul comme un pré-traitement des champs en entrée.
La boîte call-next-method a un seul outlet ramenant l'instance self, dans laquelle les champs ont été remplis par les valeurs présentées sur ses inlets. Nous effectuons maintenant un post-traitement pour affecter une valeur correcte au champ bpf. La boîte slots est une construction qui permet de lire (sur les outlets) ou d'écrire (sur les inlets) les champs d'une instance. Elle se présente exactement comme une factory. À la différence d'une factory, elle ne crée pas d'instances mais permet de consulter ou de modifier une instance existante. La boîte sur laquelle on voit une courbe est une factory de la classe bpf ; ses deux inlets d'initialisation (en sautant le premier à gauche) sont la liste des abscisses et la liste des ordonnées.
La liste des hauteurs Midi de l'accord est extraite et envoyée en entrée du champ ordonnées de la boîte bpf. En sortie de cette boîte, une nouvelle instance de bpf (contenant la courbe des hauteurs de l'accord) est affectée au champ bpf de l'objet self, qui est finalement ramené en sortie de la méthode d'initialisation.
Cette deuxième étape de calcul constitue un post-traitement : en effet, on ne pouvait construire la courbe des hauteurs qu'après la première phase d'initialisation, puisque cette dernière rajoutait une hauteur à l'accord.
Une fois la nouvelle classe définie, nous pouvons créer des boîtes factories dans un patch, ayant comme référence la nouvelle classe virchord. Nous voyons dans la Figure 2-6 un container (éditeur) de patch contenant une boîte factory pour la classe virchord. Cette boîte à 7 inlets : le premier (self) n'est pas décrit pour l'instant. Les six suivants correspondent dans l'ordre aux 5 champs hérités de la classe chord et au champ supplémentaire bpf. Nous connectons sur l'inlet lmidic une constante de liste définissant 4 hauteurs de notes. Tous les autres champs seront initialisés avec les valeurs par défaut associées.
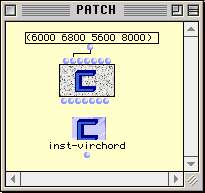
Figure 2-6 Une nouvelle factory pour la classe virchord.
L'évaluation de cette factory a pour résultat une nouvelle instance de la classe virchord, qui est visualisée en dessous par la boîte d'instance appelée inst-virchord. Étant donné qu'il existe un éditeur en notation musicale pour la classe chord, nous pouvons visualiser la nouvelle instance sous cette forme. Nous pouvons vérifier qu'une hauteur supplémentaire a bien été ajoutée dans le grave par la méthode d'initialisation.
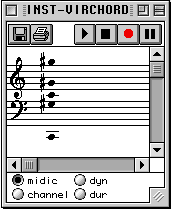
Figure 2-7 Visualisation d'un accord avec fondamentale virtuelle.
D'une façon plus générale, toute instance OpenMusic possède un éditeur par défaut appelé éditeur de structure, qui donne l'accès au différents champs, organisés selon la hiérarchie des classes :
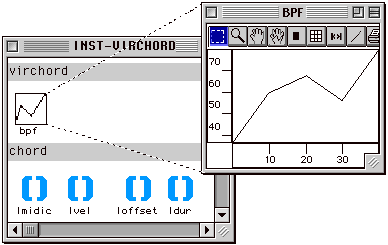
Figure 2-8 Editeur de structure d'instances.
Cet éditeur, bien que primitif, est très général dans le sens où l'on peut visualiser et éditer les valeurs de chaque champ. Comme les valeurs des champs sont visualisées comme des instances, chaque valeur possède à son tour son propre éditeur. L'édition peut se faire soit en y tapant de valeurs, soit en y glissant et déposant des objets déjà construits et compatibles avec le type du champ modifié.
Notons que nous pouvons aussi avoir accès à la valeur du champ bpf de notre instance de virchord en demandant l'évaluation sur le septième outlet de la factory.
Une boîte spécifique appelée slots est définie pour chaque classe, permettant de façon algorithmique la lecture et l'écriture des champs d'une instance.
Le premier inlet de la boîte doit recevoir via une connexion l'instance que l'on veut lire ou modifier. Les autres inlets peuvent recevoir des valeurs qui serviront à modifier les champs correspondants de l'instance. De la même façon, la lecture des valeurs des champs se fait à partir des outlets. Il est possible dans OpenMusic, de définir des méthodes propres pour la lecture et l'écriture des champs. En ouvrant le container de la boîte slots, l'utilisateur à accès au dialogue suivant :
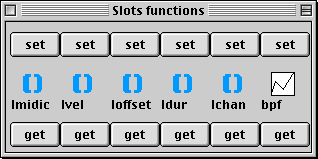
Voici une possible redéfinition de la méthode d'écriture pour le champ bpf de la classe virchord.
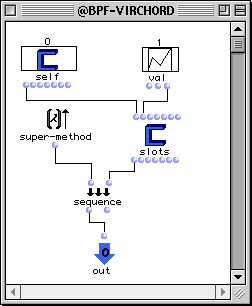
Figure 2-9 Redéfinition de la méthode d'écriture pour un champ dans une classe.
L'appel de la boîte super-method remplit le champ bpf avec la valeur val. Ensuite, une opération d'écriture sur le champ Lmidic de l'accord est réalisée en prenant comme nouvelles valeurs les coordonnées y deval. Ainsi, l'évaluation de la boîte slots dans le patch de la Figure 2-10 affecte l'instance virchord en produisant comme résultat l'accord montré dans l'éditeur (sous la forme d'arpège).
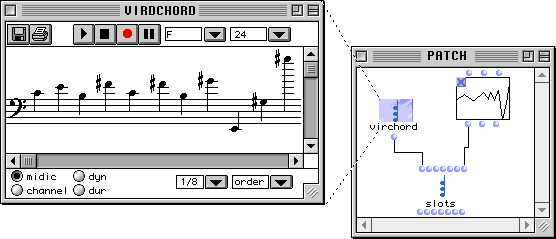
Figure 2-10 Lecture et écriture des champs d'une instance dans un patch.
Nous avons décrit la façon de définir des classes, de déclencher leur instanciation, ainsi que la lecture et l'écriture des champs d'instances. En ce qui concerne la création de méthodes pour une classe, il existe un éditeur spécifique. L'utilisateur doit spécifier pour une méthode : son nom, le nombre de sorties, la liste de paramètres spécialisateurs, le qualifieur s'il existe et le corps de la méthode sous la forme d'une connexion de boîtes similaire à un patch.
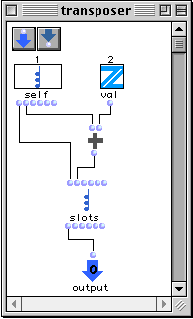
Figure 2-11 Définition d'une méthode.
Dans la Figure 2-11 nous définissons la méthode transposer avec les paramètres spécialisateurs, self de type chord et val de type entier visualisés sous la forme de représentants de classe. Cette méthode possède une unique sortie output. L'exécution de la méthode actualise le champ Lmidic de l'objet self par l'addition de l'ancienne valeur du champ Lmidic et la valeur val.
Trois cas possibles peuvent se présenter lors de l'édition d'une méthode : s'il n'existe pas une fonction générique avec le nom de la méthode, une nouvelle fonction générique est alors créée automatiquement ayant comme seule méthode celle qui est en train de se définir. S'il existe déjà une fonction générique, la méthode est additionnée à la liste des méthodes. Dans le cas où il existait une méthode ayant la même liste de spécialisateurs, cette méthode sera réécrite. Dans le deuxième cas, l'utilisateur doit spécifier : le type des paramètres spécialisateurs, le corps de la méthode et le qualifieur, par contre le nombre est imposé par la fonction générique. Le nombre d'entrées et de sorties est déterminé lors de la création de la première méthode de cette fonction. Il existe trois types des qualifieurs pour une méthode : after, before et around.
2.2.1.6 Structures de contrôle.
- Parmi l'ensemble des boîtes prédéfinies nous disposons, d'une boîte conditionnelle if correspondant à l'instruction standard trouvée dans la plupart des langages de programmation. La boîte if a trois arguments : test, action1, action2. L'évaluation d'une boîte if évalue en première instance son paramètre test. Si la valeur n'est pas nil, le résultat de l'évaluation est l'évaluation du paramètre action1, dans le cas contraire le résultat sera l'évaluation du paramètre action2.
Le patch suivant calcule la valeur absolue d'un nombre.
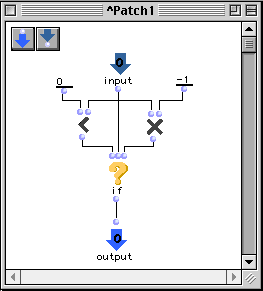
Figure 2-12 Patch avec une boîte conditionnelle.
- Une clôture lexicale peut être vue comme l'extension d'une fonction par un ensemble de variables lexicales libres auxquelles la fonction a accès en tant que variables et non comme simples valeurs. Considérons l'exemple suivant :
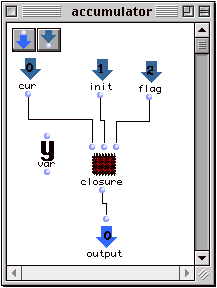
Figure 2-13 Exemple de clôture lexicale.
Le patch de la Figure 2-13 définit un accumulateur multiplicatif à trois paramètres : cur est la nouvelle valeur à accumuler, init la valeur initiale de l'accumulateur et flag est un drapeau qui suit la convention suivante : une valeur 0 initialise l'accumulateur, une valeur 1 déclenche une nouvelle accumulation et une valeur 2 lit l'état actuel de l'accumulateur. La boîte nommée var est la variable lexicale chargée de maintenir l'état de l'accumulateur. L'opération à réaliser lors de chaque évaluation de l'accumulateur est définie dans le patch interne nommé closure.
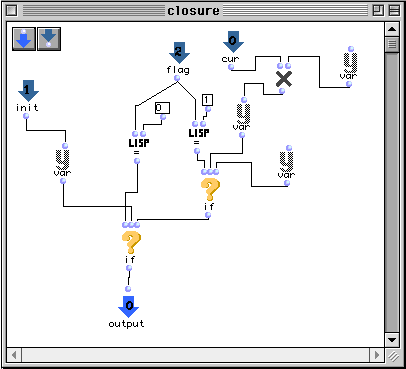
Figure 2-14 Un patch contenant des alias d'une variable lexicale.
Les boîtes appelées var sont des alias de la variable lexicale. Les alias de variables lexicales peuvent uniquement apparaître dans le patch où la variable originale est définie ou dans des patchs internes à tel patch.
Dans le patch suivant, nous avons trois boîtes de patch ayant comme référence le patch accumulator.
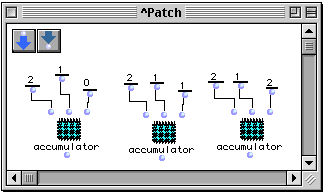
L'évaluation successive de la boîte la plus à gauche produira comme résultats 1, 1, 1,... car la seule opération faite est l'initialisation. L'évaluation de la boîte du centre produira les mêmes résultats parce que la multiplication de l'accumulateur n'est pas déclenchée. Dans ces deux cas, le premier paramètre n'est pas pris en compte. Pour la boîte la plus à droite une série d'évaluations produira comme résultats 1, 2, 4, 6...
- La construction loop permet de programmer visuellement des itérations complexes. Elle est inspirée de la macro loop de Common Lisp.
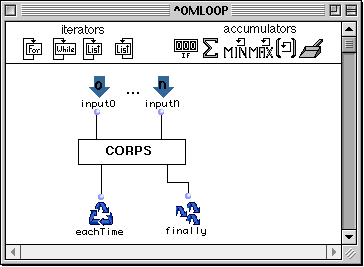
Figure 2-15 Structure d'un loop.
Un loop est constitué par :
- Un ensemble optionnel d'entrées qui permet la réception de valeurs extérieures au loop.
- Une boîte appelée eachTime qui spécifie l'action à exécuter à chaque itération du loop.
- Une boîte appelée finally qui détermine la valeur résultat de l'évaluation du loop.
- Un corps qui détermine la sémantique du loop.
Le corps d'un loop est défini par un ensemble de boîtes connectées comme dans un patch. Il existe cependant deux types de boîtes qui ne peuvent apparaître que dans un loop : les itérateurs et les accumulateurs. Ces boîtes sont disponibles dans la barre d'icônes apparaissant dans la partie supérieure de l'éditeur de loop.
Il y a quatre itérateurs dans OpenMusic :
- For avec les paramètres begin, end et step. Itère entre les valeurs begin et end en avançant à chaque itération d'une valeur de step.
- While avec le paramètre test. Itère tant que le test test est satisfait.
- Inlist avec le paramètre list. Itère pour chaque élément sur la liste list.
- Onlist avec le paramètre list. Itère pour chaque cdr sur la liste list.
Les accumulateurs définissent une opération binaire entre l'état interne courant de l'accumulateur et une nouvelle valeur en entrée. Le résultat de cette opération est écrit dans l'état de l'accumulateur. Les accumulateurs dans un loop peuvent être généralisés par la boîte :
Où le paramètre d'entrée représente la nouvelle valeur et les trois sorties évaluent l'accumulateur en suivant la convention suivante : la première sortie effectue le calcul avec le paramètre d'entrée et actualise l'état de l'accumulateur, la deuxième sortie retourne l'état actuel de l'accumulateur sans effectuer une accumulation et la troisième sortie réinitialise l'accumulateur. Il existe cinq accumulateurs spécifiques qui diffèrent dans la fonction appliquée, ces accumulateurs sont :
- x-append , qui ajoute la nouvelle valeur à la fin d'une liste initialisée avec nil.
- min, qui calcule le minimum entre l'état et la nouvelle valeur.
- max, qui calcule le maximum entre l'état et la nouvelle valeur.
- count, qui incrémente d'une unité l'état si la nouvelle valeur est non nil.
- add, qui fait l'addition entre l'état et la nouvelle valeur.
Il existe un accumulateur général représenté par la boîte :
Dans cette boîte, les paramètres de sortie suivent la convention déjà donnée. Deux nouvelles entrées sont visualisées dans cette boîte : la première pour spécifier la valeur initiale et la deuxième pour spécifier la fonction à exécuter à chaque accumulation. Nous pouvons spécifier cette fonction, soit par un symbole de fonction (lisp ou générique), soit par une boîte avec visualisateur d'état en mode lambda (comme on le verra ultérieurement).
Voici un exemple de loop, élaboré par le compositeur Mikhail Malt qui définit la multiplication de deux accords.
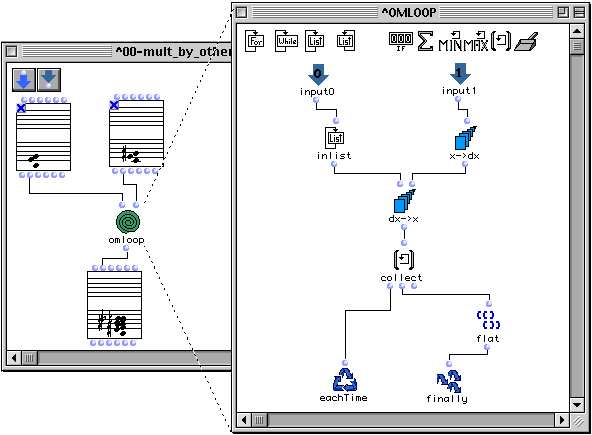
Figure 2-16 Une multiplication de deux accords.
- Boîtes avec visualisateur d'état en mode lambda.
L'évaluation d'une boîte avec visualisateur d'état en mode lambda ramène l'équivalent d'une lambda-expression plutôt que le résultat d'une application fonctionnelle. Ce mode sera donc utilisé à chaque fois que l'on branche la sortie d'une boîte à l'entrée d'une fonctionnelle. L'évaluation d'une boîte avec visualisateur d'état en mode lambda est indépendant de la référence de la boîte (un patch, une fonction générique, une fonction Lisp, une classe, etc.).
La règle suivante nous montre l'évaluation d'une boîte en mode lambda (R15') :
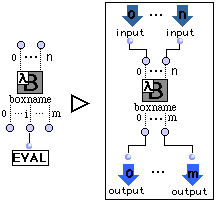
- La currification permet de transformer une fonction f à n
arguments a1,...,an en une fonction f' à
k arguments, q1,...,qk avec k <= n, 
. Le reste des paramètres de
f non utilisés par f' est spécifié par des
constantes qui sont substituées à ces paramètre
dans le corps de f'. La currification est très utile, par
exemple pour le cas des accumulateurs de loop, lorsque l'on
veut spécifier comme fonction d'accumulation une fonction
d'arité plus grande que 2. Dans OpenMusic, on utilise le mode
de boîte lambda pour currifier : les inlets sans
connexion constituent les qj ; les inlets ayant une valeur
en entrée sont considérés comme des constantes.
Nous donnons une nouvelle règle pour les boîtes en mode lambda en incluant la currification (R15) :
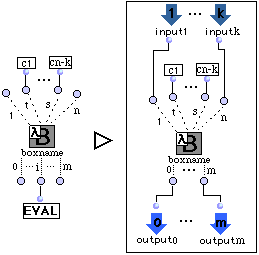
- Récursivité .
La double représentation de patchs et de fonctions génériques sous la forme de vues et de containers offre la possibilité d'utiliser comme référence d'une boîte, dans un container, la fonction ou le patch associée à ce même container. Ceci permet de représenter aisément la récursivité, un container de patch, par exemple, pouvant contenir une boîte de patch ayant la même référence.
L'exemple typique de fonction récursive est la fonction factorielle, qui peut être définie en OpenMusic par le patch suivant.
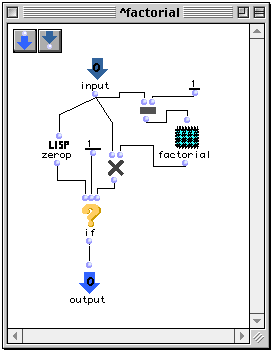
Figure 2-17 Un patch récursif.
- Boîtes avec visualisateur d'état en mode 1.
L'évaluation d'une boîte avec visualisateur d'état en mode 1 nous permet de simuler l'instanciation locale de manière graphique. L'évaluation d'une boîte en mode 1 est équivalente à l'expression : let x=A in B où A est le résultat de l'évaluation de la boîte en mode normal et B est le contexte de l'évaluation.
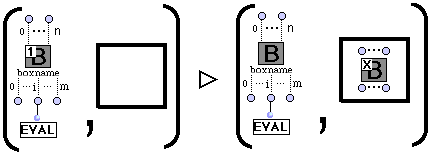
Pour résumer les différentes modes d'évaluation d'une boîte, l'exemple suivant nous semble pertinent :
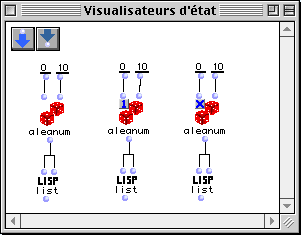
Figure 2-18 Modes d'évaluation d'une boîte.
Dans le patch de la Figure 2-18, nous avons trois boîtes ayant comme référence la fonction aleanum et avec différents modes d'évaluation.
L'évaluation successive de la boîte appelée list la plus à gauche produira comme résultats : (0 6),(1 8),(0 7),... L'évaluation de la boîte du centre produira des paires avec les mêmes résultats (5 5),(4 4),(8 8),... cela provenant du fait que la boîte ne s'évalue qu'une fois pendant l'évaluation du patch. Pour la boîte la plus à droite une série d'évaluations produira toujours le même résultat (4 4),(4 4),(4 4),...
OpenMusic a été implémenté sur le langage CLOS et est actuellement disponible pour la plate-forme Apple Macintosh. Nous rappelons les critères qui ont dirigé ce choix :
- C'est un langage fonctionnel et objet puissant, bien défini, disposant d'un modèle formel solide [Cast98].
- CLOS et Common Lisp ont fait l'objet d'une normalisation internationale et ont un excellent degré de portabilité [Stee98].
- Des librairies graphiques orientées objet existent sur toutes les plate-formes.
- Une énorme quantité de savoir-faire en informatique musicale (et notamment toute l'expérience de l'Ircam depuis PreForm et PatchWork) est associée à ce langage.
- Le modèle de fonction générique constitue une bonne intégration des aspects fonctionnels et objet.
- L'accès à la méta-programmation facilite le type d'extension que nous voulons réaliser.
Le système de méta-programmation disponible en CLOS contient une partie statique consistant en une hiérarchie de classes de méta-objets et une partie dynamique ou protocole de méthodes, qui permet la manipulation des méta-objets. Nous entendons par méta-objets les divers éléments du système objet sous-jacent à CLOS, tels que les fonctions génériques, les méthodes, les variables d'instances (slots) et les classes. Les deux tâches principales du méta-programmeur sont : définir des sous-classes des classes de méta-objets et définir ou redéfinir des méthodes pour ces nouvelles classes ou celles déjà existantes [Paep93]. C'est cette technique que nous avons utilisée pour implémenter OpenMusic. En général, on utilise la méta-programmation en vue de deux objectifs particuliers : soit on décide d'ajuster la performance du système pour une application spécifique, soit on enrichit la sémantique du langage avec des caractéristiques spécifiques. Notre intérêt concerne plutôt cette deuxième option.
Dans cette optique, on peut considérer OpenMusic comme un enrichissement de la syntaxe et de la sémantique de CLOS par méta-programmation , plus certaines entités visuelles, telles que patch ou boîte qui n'ayant pas de correspondant dans CLOS, ne peuvent être constituées par méta-programmation (en effet, il n' y a pas de classe permettant de réifier la notion de programme ou d'invocation fonctionnelle dans CLOS).
Nous ne ferons pas une description détaillée de CLOS, le lecteur peut consulter [stee98] et [Paep93]. Nous montrons cependant une partie de la hiérarchie de classes de méta-objets dans CLOS nécessaire à la compréhension de notre implémentation :
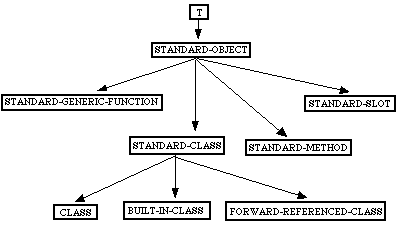
Figure 2-19 Hiérarchie de classes de méta-objets dans CLOS.
Pour implémenter OpenMusic, nous avons décidé d'opérer la même division que CLOS entre une partie statique et une partie dynamique. L'un des problèmes décisifs dans notre conception a été le niveau de détail auquel on définit le protocole ; en général, un protocole très détaillé est peu modulaire ; ainsi les changements doivent être effectués en plusieurs endroits, ce qui affecte la fiabilité. Par contre un protocole peu détaillé rend délicat le choix de l'endroit où introduire les modifications.
La figure suivante illustre la partie statique d'OpenMusic. Les classes de méta-objets CLOS sont représentées par un rectangle à double épaisseur de ligne.
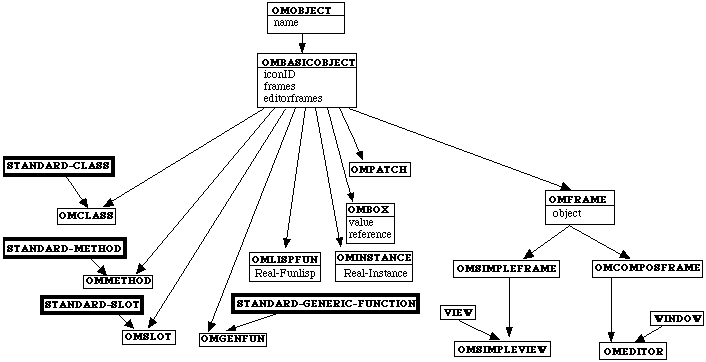
Figure 2-20 Hiérarchie de classes de méta-objets dans OpenMusic.
Cette hiérarchie de classes rend compte de tous les objets manipulables dans l'environnement visuel et dans le langage de programmation visuel d'OpenMusic. Les classes fondamentales du système objet visuel d'OpenMusic, OMClass, OMMethod, OMSlot et OMGenFun, héritent d'une part de la classe OMObject et d'autre part d'une classe fondamentale CLOS homologue. Les classes OMPatch et OMBox réifient respectivement les notions de patch et de boîte inexistantes dans CLOS. La classe OMLispFun (qui réifie la notion de fonction Lisp simple – non générique), ne peut être constituée par méta-programmation. Car la classe fondamentale CLOS homologue function constitue une primitive qui n'est pratiquement pas sous-classable. Dans ce cas précis, nous opérerons par une sorte de délégation en agissant sur le champ Real-FunLisp qui contient un pointeur vers la fonction Lisp. Une dernière classe, OMInstance, est introduite afin de visualiser les instances en général. De même que pour les fonctions Lisp, le champ Real-Instance d'une OMInstance contient un pointeur vers l'instance CLOS. Les huit classes mentionnées, constituent les objets de calcul de notre langage (partie gauche de l'arbre d'héritage Figure 2-20). La partie droite de l'arbre d'héritage implémente le paradigme visuel. On peut noter que la classe OMFrame hérite aussi de la classe OMBasicObject. Cela signifie que le paradigme visuel fait partie du langage, ceci étant fait dans l'intention de permettre à l'utilisateur de modifier et de contrôler ce paradigme.
Tout OMObject a un nom (name) et peut être visualisé sous deux formes, soit comme une vue simple ou comme un éditeur. Un éditeur est une instance de la classe OMEditor, tandis qu'une vue est une instance de la classe OMSimpleView. Tout objet de visualisation (instance de la classe OMFrame) est fortement attaché à un objet de calcul. Ce lien est exprimé par le champ object de la classe OMFrame. Les objets de calcul, à leur tour, possèdent deux champs, frames et editorframes, qui contiennent respectivement une liste des vue simples et un éditeur actuel qui visualisent l'objet en question. Nous allons détailler cette interaction entre objets de calcul et objets visualisateurs dans la section suivante.
Nous allons faire une description de la partie dynamique de notre langage, on remarquera la simplicité de ce protocole. Nous n'envisageons pas la réécriture d'autres langages ou applications à partir d'une modification de notre langage, cependant un exemple de méta-programmation graphique est donné dans 2.2.2.3.
Les quatre fonctions génériques suivantes peuvent être utilisées par le développeur qui voudrait introduire de nouvelles visualisations pour les objets de base.
- get-vues : OMBasicObject ® liste de sous-classes d'OMSimpleFrame.
La fonction get-vues retourne une liste avec les classes de vues possibles pour un objet donné.
- get-containers : OMBasicObject ® liste de sous-classes d'OMComposFrame
La fonction get-containers retourne une liste avec les classes d'éditeurs possibles pour un objet donné.
- type-of-view : OMComposFrame ® entier.
Cette fonction retourne un indice servant à déterminer le type de vue qui contiendra le OMComposFrame passé comme paramètre.
- OpenEditorframe : OMBasicObject ´ entier ® OMComposFrame.
S'il existe déjà un éditeur pour l'OMBasicObject dans son champ editorframes, alors la fonction générique OpenEditorframe vérifie si la position de l'éditeur sur la liste (get-containers OMBasicObject) est égale à l'indice i. Si c'est le cas, on rend cet éditeur actuel. Si l'indice est différent, on ferme l'éditeur actuel et l'on rend actuel l'éditeur de la position i sur la liste d'éditeurs. En général, les éditeurs sont ouverts par un événement de double click de souris sur la vue d'un OMBasicObject. Le paramètre i est en rapport avec un événement de clavier (e.g. command = 0, shift = 1, alt = 2, etc.).
Dans notre modèle, les objets sont composés par un ensemble d'éléments et optionnellement par des relations entre eux. Par exemple, une classe est une liste ordonnée des champs, une fonction générique consiste en un ensemble de méthodes, un patch contient une liste de boîtes connectées, etc. Une fonction fondamentale dans notre système est donc la fonction get-elements, celle-ci retournant pour chaque OMBasicObject la liste de ses éléments.
- get-elements : OMClass ® liste de OMSlots.
get-elements : OMPatch ® liste de OMBox.
get-elements : OMGenFun ® liste de OMMethods.
get-elements : OMMethod ® liste de OMBox.
get-elements : OMComposFrame ® liste de OMSimpleFrame.
Le mécanisme de glisser-déposer est le principal outil d'édition dans OpenMusic. Une opération de glisser-déposer est définie comme une action entre une instance de la classe OMsimpleView appelée "source" et une instance de la classe OMEditor appelée "cible". Il existe un ensemble de prédicats allow-drop qui déterminent si l'opération de glisser-déposer est possible entre une paire (source , cible).
Les fonctions add-element et remove-element plus les mécanismes de glisser-déposer et de délégation définissent le paradigme d'édition d'objets.
- add-element : OMClass ´ OMSlot ® OMClass.
add-element : OMPatch ´ OMBox ® OMPatch.
add-element : OMGenFun ´ OMMethod ® OMGenFun.
add-element : OMMethod ´ OMBox ® OMMethod.
add-element : OMComposFrame ´ OMSimpleFrame ® OMComposFrame.
- remove-element : OMClass ´ OMSlot ® OMClass.
remove-element : OMPatch ´ OMBox ® OMPatch.
remove-element : OMGenFun ´ OMMethod ® OMGenFun.
remove-element : OMMethod ´ OMBox ® OMMethod.
remove-element : OMComposFrame ´ OMSimpleFrame ® OMComposFrame.
Glisser une vue dans un éditeur produit en général, l'application de la fonction générique add-element aux paramètres cible et source. Cette fonction est chargée d'effectuer les modifications visuelles dans l'éditeur, elle doit aussi déléguer l'invocation de la fonction add-element au couple formé par les champs object de cible et de source. Cette dernière invocation est chargée de modifier l'objet de calcul visualisé par l'éditeur. Les fonctions suivantes, qui complètent le protocole ainsi que la fonction remove-element, suivent le même paradigme :
- rename : Obj ´ name ® Obj.
Change le nom d'Obj par name .
- change-icon : Obj ´ iconID ® Obj.
Change l'icône d'Obj par iconID.
- select : Obj ® Obj.
Sélectionne Obj.
- unselect : Obj ® Obj.
Désélectionne Obj.
- moveobject : Obj ´ position ® Obj.
Change la position d'Obj à position.
- connec : SourceBox ´ i ´ TargetBox ´ j ® Bool.
Connecte la i-eme sortie de la boîte SourceBox à la j-eme entrée de la boîte TargetBox.
- box-value : Box ´ i ® Obj.
Evalue la i-eme sortie de la boîte Box.
2.2.2 L'environnement de programmation OpenMusic.
De même que dans PW et la plupart des environnements graphiques, OpenMusic est basé sur la notion d'événement. Les containers qui constituent l'environnement à un instant donné sont des fenêtres. Chaque fenêtre doit traduire les événements (principalement, click de souris, événements du clavier et glisser-déposer) en actions spécifiques sur les containers. Ceux-ci à leur tour peuvent déléguer l'action aux vues les constituants. Ce mécanisme ne diffère pas trop du mécanisme expliqué dans le numéral 1.3.2.1. Dans cette section, nous nous limitons à la description des divers objets constituant l'environnement de programmation.
2.2.2.1 Description des méta-objets de l'environnement.
La figure suivante montre l'arbre de hiérarchie de classes pour les objets de l'environnement.
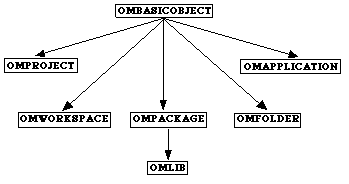
Figure 2-21 Hiérarchie de classes des objets de l'environnement dans OpenMusic.
Nous procédons à la description de chaque objet, ainsi qu'à leur visualisation sous la forme de vues et de containers.
L'interface principale dans OpenMusic est le workspace. Le workspace est un gestionnaire d'icônes qui essaie de copier le modèle du finder Macintosh. La vue d'un workspace est définie par le cadre simple illustré dans la figure suivante :
Plusieurs workspaces indépendants peuvent être gardés dans un même environnement, cependant un seul workspace peut être visualisé sous la forme de container à un instante donné. Ce workspace est appelé le workspace actuel. La figure suivante montre un workspace sous la forme de container.
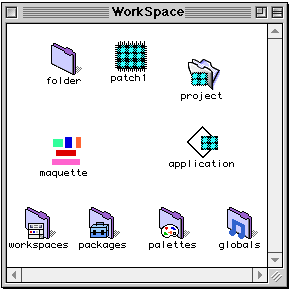
Figure 2-22 Un container de workspace.
Tous les objets inclus dans un workspace (i.e. patchs, maquettes, folders, projects, applications et folders spéciaux) sont persistants. La gestion de fichiers est transparente pour l'utilisateur, ainsi que l'exportation et l'importation d'objets, se faisant à l'aide du mécanisme de glisser-déposer.
Il existe divers niveaux dans la structure graphique d'une conception musicale. Dans OpenMusic, le patch est l'unité de programme. Un patch peut à son tour être condensé en un icône et devenir à son tour un atome de calcul dans un autre patch. Premier aspect récursif dont on jouera pour montrer ou cacher la complexité. La programmation devient alors un art graphique par lequel on essaiera de rendre évidents les aspects syntaxiques et sémantiques.
En plus des patchs, le compositeur a recours à la notion d'objet. Un objet est une instance d'un autre objet que l'on appelle une classe. Les objets créés directement par l'utilisateur ou résultats d'un calcul peuvent être matérialisés : ils émergent littéralement à la surface du patch, sous formes de nouveaux icônes, et deviennent des sources de valeur ou des lieux de stockage d'information. Un objet peut ainsi être un simple nombre, un texte ou une polyphonie à vingt-quatre voix. Si on prend aussi en compte d'autres structures graphiques telles que les maquettes ou les applications, nous nous apercevons que le workspace est une nécessité fondamentale pour permettre au compositeur de développer son travail dans différentes directions par rapport à la complexité et à la spécificité de ses constructions.
Les folders permettent l'organisation des divers objets en une structure hiérarchique. La vue d'un folder est représentée dans le graphique suivant.
Le container d'un folder est identique au container des workspaces, la seule différence réside dans le fait que les folders ne peuvent pas contenir les folders spéciaux que nous décrirons par la suite.
Un package peut être considéré comme un type particulier de folder permettant de garder des classes et des fonctions génériques ainsi que d'autres sous-packages. La vue d'un package est montrée dans la figure suivante.
La représentation d'un package sous forme de container sort un peu du schéma traditionnel. En réalité, le container d'un package est un ensemble de containers, chacun regroupant par type les divers éléments du package. Nous n'allons pas entrer dans la formalisation de cet éditeur, un exemple nous semble assez explicatif. Dans la Figure 2-23, on voit que l'éditeur d'un package contient trois containers : le premier, en allant de gauche à droite, montre les différents sous-packages et les classes appartenant au package. Le container du milieu permet de visualiser l'ensemble de fonctions génériques d'un sous-package sélectionné. Le dernier container est formé par la collection des méthodes d'une fonction générique sélectionnée.
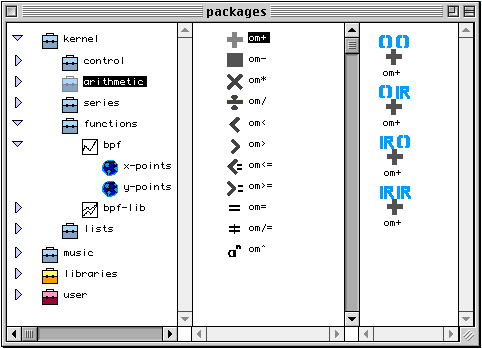
Figure 2-23 Un container de package.
Notons dans la Figure 2-23, l'existence d'un package spécifique appelé user qui est l'endroit où l'utilisateur peut définir et garder ses classes et fonctions génériques. Il existe aussi un autre package spécifique appelé libraries qui correspond à la notion expliquée dans 1.3.2.3.
Un autre éditeur existe pour les packages, il permet de visualiser l'arbre de hiérarchie des classes.
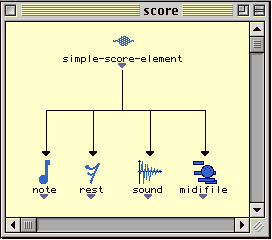
Figure 2-24 Arbre de hiérarchie des classes d'un package.
Les classes appartenant à d'autres packages (simple-score-element), sont visualisées par des alias.
Les palettes sont simplement des raccourcis graphiques qui permettent à l'utilisateur de chercher les classes et les fonctions génériques ailleurs que dans le folder spécial de packages. L'utilisateur peut créer ses propres palettes dans le folder spécial palettes qui se trouve dans le workspace. Une palette est visualisée sous cette forme de vue :
Le container d'une palette est une fenêtre flottante contenant des vues de classe ou des fonctions génériques.
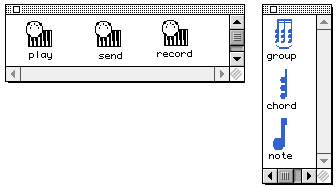
Ce folder spécial, qui se trouve dans le workspace, permet le partage d'instances entre différents patchs. Une instance créée dans un patch (voir 2.2.1.5.) devient globale si elle est déposée dans le folder globals. Dans ce cas, la boîte qui représente l'instance dans le patch devient une boîte d'instance globale, c'est-à-dire, une boîte dont la référence est la nouvelle instance créée dans le folder globals. De même, glisser une instance du folder globals vers un patch a pour effet la création d'une nouvelle boîte d'instance globale dans le patch. Le container du folder globals est montre dans la prochaine figure.
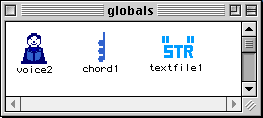
Un projet est un constructeur d'interface qui rend possible la création d'objets de type application. La figure suivante montre un projet sous forme de vue.
L'éditeur d'un projet consiste en une fenêtre dans laquelle l'utilisateur dispose d'items de divers types. Les items d'un projet sont mis en relation à l'aide d'un patch spécial. Pour mieux comprendre un projet examinons l'exemple suivant.
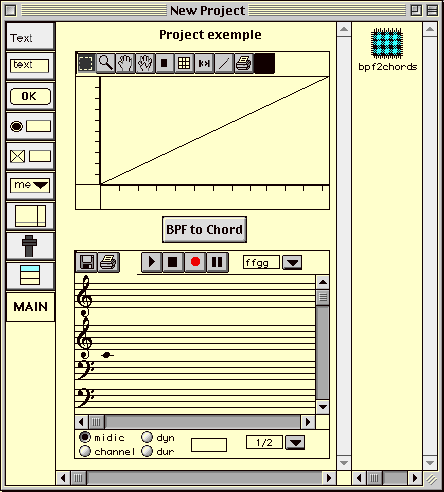
Figure 2-25 Le container d'un projet.
Nous pouvons remarquer quatre éléments principaux dans le container d'un projet :
- Un espace dédié à la visualisation de l'ensemble des patchs définissant les algorithmes qui seront exécutés. Dans notre exemple, nous allons nous servir d'un patch qui à partir d'une fonction par segments (bpf) construit une séquence de notes (voir annexe II.2). Le nombre de patchs pour chaque projet est illimité.
- Une palette contenant divers types d'items prédéfinis (i.e. textes, boutons, sliders, menus, etc.).
- Un container principal où l'utilisateur dispose les différents items qui constituent le projet. À part les items contenus dans la palette, l'utilisateur peut glisser des classes pourvu qu'elles aient un éditeur défini. Dans notre exemple, il y a un item éditeur de la classe bpf et un autre de la classe chord-seq.
- Un patch de relation qui est accessible à partir du bouton MAIN de la palette.
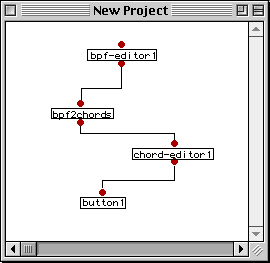
Figure 2-26 Un patch de relation dans un project.
Le patch de relation détermine la façon dont on déclenche les algorithmes, le calcul des valeurs d'entrée et la visualisation des résultats. Il est important de noter que le patch de relation suit une sémantique différente de celle définie dans 2.2.1.3. Nous n'allons pas détailler formellement le patch de relation ni les boîtes qui représentent les items du project. Nous montrons à titre d'exemple, le patch de relation du projet de la Figure 2-25. Le patch de relation de la Figure 2-26 exprime qu'à chaque fois que le bouton est poussé, la valeur de l'éditeur de bpf est prise comme paramètre pour l'évaluation du patch bpf2chord.Et que la valeur résultant de cette évaluation sera visualisée dans l'éditeur chord-seq.
L'option de menu make-application pour un projet, produit un fichier de code Lisp compilé qui est associé à un nouvel objet de type application et que nous décrirons ensuite.
Nous utilisons le terme application pour dénoter des objets qui exécutent une action déterminée sans besoin de patchs, de classes ou de fonctions génériques définies par l'utilisateur. Il nous faut toutefois dire que les applications d'OpenMusic ne correspondent pas au sens traditionnel d'application stand-alone. Le graphique suivant montrée la visualisation d'une application sous la forme de vue.
Un événement de double click sur la vue d'une application évalue le fichier Lisp associé à elle. Pour l'exemple montré dans la section précédente, l'application affichera la fenêtre suivante :
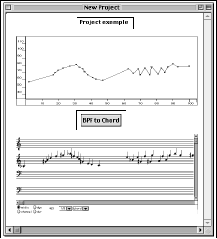
Figure 2-27 Une application OpenMusic.
L'utilisateur pourra, ainsi dessiner sa courbe dans l'éditeur de bpf et en appuyant sur le bouton BPFtoChord une séquence de notes sera affichée dans l'éditeur musical. Les résultats obtenus dans une application peuvent être utilisés dans un patch à l'aide du mécanisme de glisser-déposer. Les applications offrent un paradigme intéressant pour l'échange de travaux entre utilisateurs, ainsi que pour le masquage de la complexité de certains algorithmes qui peuvent être plus simples à écrire en Lisp.
Nous avons vu dans le numéral 2.2.2.1 que les différentes classes de méta-objets (workspace, folder, package, etc.) héritent de la classe OMBasicObject. Les objets de l'environnement de la même façon que les entités du calcul (classes, méthodes, etc.) peuvent être visualisés sous forme de vues (instances de la classe OMSimpleView) ou sous forme d'éditeurs (instance de la classe OMEditor). Ainsi le protocole défini dans 2.2.1.7, constitué par les fonctions génériques get-elements, add-element, remove-element, rename, etc., est élargi avec des méthodes spécialisées pour chaque objet de l'environnement. Voici par exemple la fonction add-element :
- add-element : OMWorkSpace ´ OMFolder ® OMWorkSpace
add-element : OMWorkSpace ´ OMProject ® OMWorkSpace
add-element : OMWorkSpace ´ OMApplication ® OMWorkSpace
add-element : OMWorkSpace ´ OMPatch ® OMWorkSpace
add-element : OMPackage ´ OMClass ® OMPackage
add-element : OMPackage ´ OMGenFun ® OMPackage
add-element : OMPackage ´ OMPackage ® OMPackage
- add-element : OMFolder ´ OMFolder ® OMFolder
add-element : OMFolder ´ OMProject ® OMFolder
add-element : OMFolder ´ OMApplication ® OMFolder
add-element : OMFolder ´ OMPatch ® OMFolder
2.2.2.3 Protocole graphique des méta-objets.
Nous avons pu étendre CLOS grâce au protocole de méta-objets. De même, l'utilisateur peut introduire de nouvelles caractéristiques (e.g. typage des sorties d'une méthode) ou changer la sémantique des actions basiques (e.g. une connexion) dans OpenMusic en utilisant le protocole graphique de méta-objets.
Il existe un sous-package appelé meta qui montre les parties dynamique et statique de notre langage. Nous pouvons observer dans la Figure 2-28 les diverses classes de méta-objets, les champs les constituant et les fonctions génériques qui définissent le protocole.
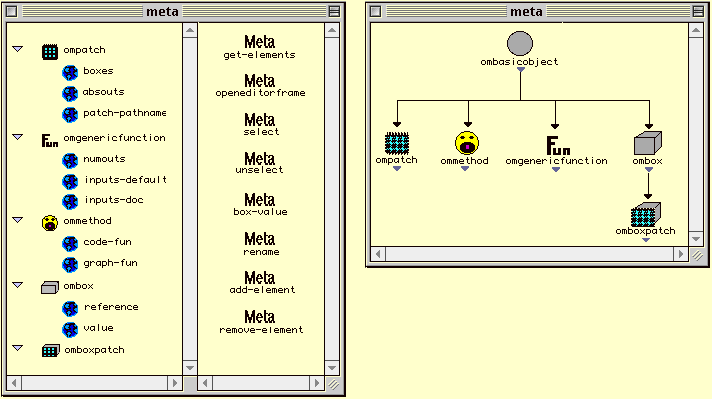
Figure 2-28 Le package méta dans OpenMusic.
La classe OMBoxPatch est une sous-classe de OMBox dont les instances sont les boîtes d'invocation de patch.
Dans l'exemple de la Figure 2-29, nous rajoutons des méthodes à la fonction générique box-value chargée de l'évaluation de chaque boîte. La définition visuelle de ces trois méthodes change le comportement du langage en introduisant un suivi visuel de l'évaluation de chaque patch. La première méthode définie avec qualificateurbefore sélectionne la boîte avant son exécution. La deuxième méthode avec qualificateur after désélectionne la boîte après son évaluation. Finalement la méthode définie pour les boîtes de patch (instances de la classe OMBoxPatch) ouvre l'éditeur du patch référence de la boîte ; appelle la fonction box-value avec comme paramètre, la boîte absout correspondant à la sortie du patch évaluée (afin de visualiser les boîtes à l'intérieur du patch) et finalement déclenche l'évaluation.
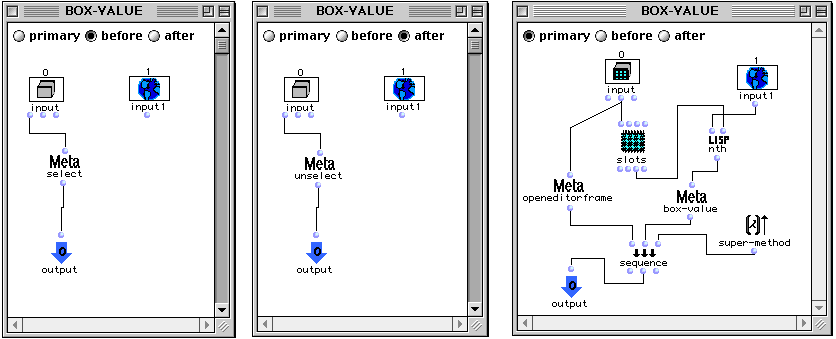
Figure 2-29 Un exemple de méta-programmation graphique.
Les trois méthodes de la Figure 2-29 sont des instances courantes de OMMethod, la seule chose qui les particularise est leur spécialisation par les classes de méta-objets OMbox et OMBoxPatch. Comme on pouvait le supposer, une grande partie des boîtes dans le corps des méthodes ont comme référence des fonctions génériques appartenant au protocole défini dans 2.2.1.7. (select, box-value, openeditorframe, etc.).
Le sous-classage des classes de méta-objets se réalise en suivant le schéma traditionnel décrit dans 2.2.1.5. Pour créer des méta-objets avec les nouvelles classes, l'utilisateur dispose d'une fenêtre de préférences permettant de déposer la vue de la classe qui instanciera les nouveaux méta-objets.
Figure 2-30 Dialogue de préférences pour les classes de méta-objets.
Dans l'exemple suivant nous allons créer une nouvelle classe de méta-objet appelée Typed-Method qui hérite de la classe prédéfinie OMMethod.
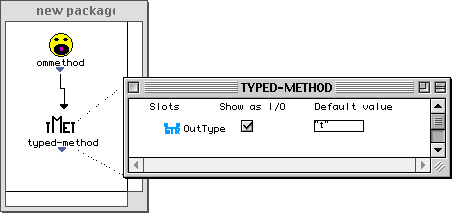
Figure 2-31 Une nouvelle classe de méta-objet définie par héritage.
Même si Typed-Method est une classe des méta-objets, elle reste une classe standard d'OpenMusic. Dans le container de Typed-Method, nous ajoutons un champ appelé OutType où nous allons garder, sous forme d'une chaîne de caractères, le type de sortie de la méthode.
Étant donné que Typed-Method est une sous-classe d'OMMethod, nous pouvons glisser cette classe dans la fenêtre de la Figure 2-30 puis la déposer sur l'icône "meta-class-method". Après cela, la définition graphique des nouvelles méthodes produira des instances de la classe Typed-Method, qui auront un champ pour lire et écrire leur type de sortie.
Nous pouvons aussi de manière graphique ajouter de nouvelles fonctions génériques au protocole des méta-objets. Dans la Figure 2-32, nous définissons les méthodes get-type spécialisées par une méthode standard et une méthode de la classe Typed-Method. Ces deux nouvelles méthodes peuvent éventuellement être des instances de la classe Typed-Method...
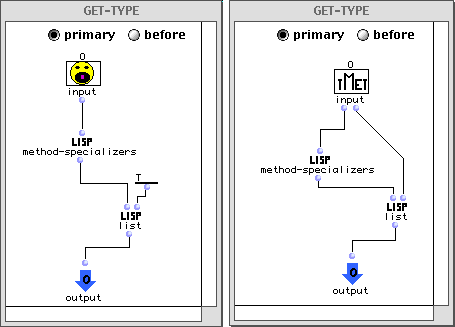
Figure 2-32 Définition d'une nouvelle fonction générique pour le protocole de méta-objets.
Nous pouvons, en suivant la définition donnée dans la section dédiée au l&-calcul, donner une définition du type d'une fonction générique.
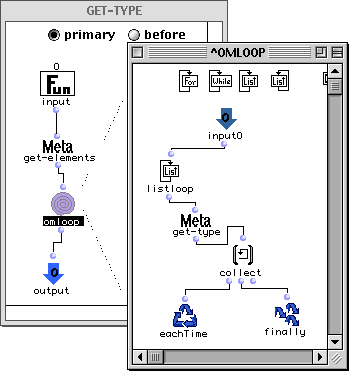
Figure 2-33 Définition du type d'une fonction générique.
Nous n'avons pas l'intention de définir un système de types pour CLOS (nous sommes conscients de la difficulté de la tâche). Nous voulons simplement montrer qu'il est possible de manière entièrement graphique de changer la sémantique des actions basiques. Nous pouvons par exemple, définir de nouvelles méthodes pour la fonction "connect" où l'on ferait un test de compatibilité de type avant de permettre la connexion.
2.2.3 Le framework musical OpenMusic.
" A framework is a set of cooperating classes that make up a reusable design for a specific class of software " [GHJV95]. Un framework implique plus que la réutilisation de code. Dans un framework, l'utilisateur réutilise aussi la conception. L'utilisation d'un framework n'est pas seulement une question d'économie de ressources, nous pensons que l'un des avantages majeurs est l'homogénéité des structures entre différentes applications. Pour cela, il faut réfléchir à un compromis entre généralité et fonctionnalité. Nous allons décrire l'ensemble des classes musicales données a priori par OpenMusic, ainsi qu'une partie de l'ensemble des fonctions génériques agissant sur ces classes.
Les classes musicales se trouvent dans le package music-score, dont on montre le container sous forme d'un arbre de hiérarchie de classes.
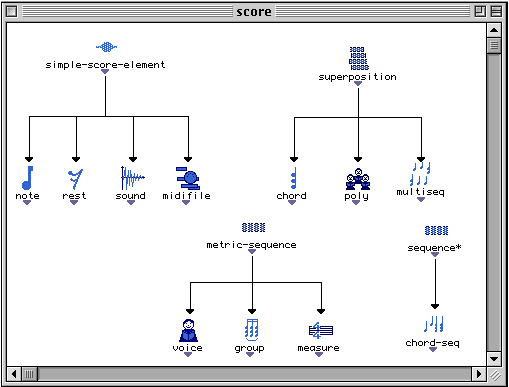
Figure 2-34 Hiérarchie de classes musicales.
Une brève description des champs de chaque classe va être faite.
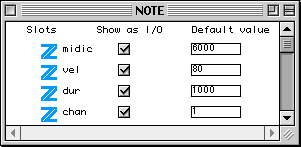
- midic. Exprime la hauteur de la note en midicents (midi * 100).
- vel. L'intensité de la note est un nombre compris entre 0 et 127.
- dur. La durée exprimée en millièmes de secondes.
- chan. Un nombre de canaux midi compris entre 1 et 16.
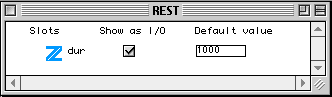
- dur. La durée du silence exprimée en millièmes de secondes.
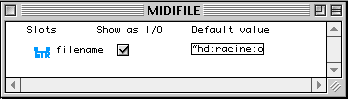
- filename. Une chaîne de caractères spécifiant l'adresse du fichier Midi.
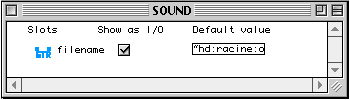
- filename. Une chaîne de caractères spécifiant l'adresse du fichier AIFF.
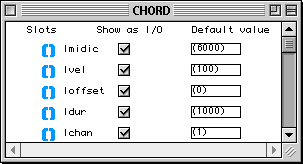
- Lmidic. Une liste de midicents.
- Lvel. Une liste de nombres compris entre 0 et 127.
- Loffset. Une liste de nombres compris entre 0 et 127.
- Ldur. Une liste de durées.
- Lchan. Une liste de canaux midi.
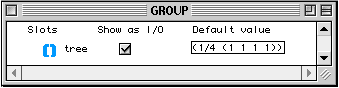
- tree. Une liste représentant un arbre rythmique (voir la section suivante).
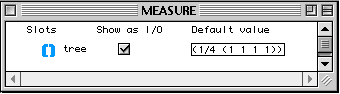
- tree. Une liste représentant un arbre rythmique.
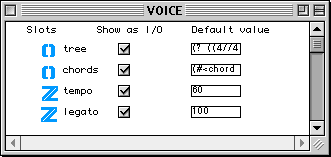
- tree. Une liste représentant un arbre rythmique.
- chords. Une liste d'accords.
- tempo. Le tempo.
- legato. Une valeur entre 0 et 100. 0 signifie que la durée des accords doit correspondre avec les durées précisées dans la liste d'accords. 100 signifie que les durées des accords sont conditionnées par l'onset de l'accord suivant.
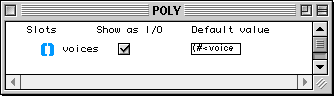
- voices. Une liste de voices.
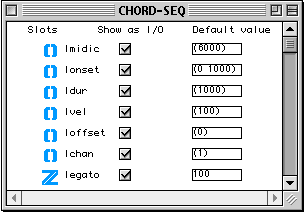
- Lmidic. Une liste de midicents.
- LOnset. Une liste avec le temps d'attaque de chaque accord (en millièmes de secondes)
- Ldur. Une liste de durées.
- Lvel. Une liste de nombres compris entre 0 et 127.
- Loffset. Une liste de nombres compris entre 0 et 127.
- Lchan. Une liste de canaux midi.
- legato. Une valeur entre 0 et 100. 0 signifie que la durée des accords doit correspondre avec les durées précisées dans la liste d'accords. 100 signifie que les durées des accords sont conditionnées par l'onset de l'accord suivant.
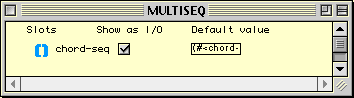
- Chord-seqs. Une liste de sequences d'accords.
Certaines classes ont besoin d'un arbre rythmique. Celui-ci n'est qu'une liste de la forme (D,S) où D est un nombre (entier ou fractionnaire) qui exprime l'extension temporelle de l'objet rythmique représenté et S est une liste d'items qui définissent un ensemble de proportions en D. Chaque item appartenant à D peut être soit un numéro ou un arbre rythmique.
L'arbre rythmique (1 (1 1 1 1)) représente une structure durant une ronde qui est divisée en quatre temps égaux, chaque temps a une durée d'une noire. La liste (2 ( (1 (1 1 1 1)) (1 (1 1 1 1)) ) équivaut à une structure rythmique qui dure une blanche, divisée en deux groupes, chaque groupe contient quatre double-croches et leur durée est d'une noire. Quand la valeur D est un fractionnaire, la structure rythmique spécifiée est une mesure ; dans ce cas D détermine la signature de la mesure, par exemple 4/4 ou 6/8. Afin d'épargner des calculs ennuyeux à l'utilisateur, D peut être remplacé par le symbole '?'. Dans ce cas, OM calcule la valeur de D dépendante de l'information contenue dans S.
La figure suivante nous montre une voix à deux mesures correspondant à l'arbre rythmique (? ((4//4 (1 (1 (1 -2 1 1)) 1 1)) (4//4 (1 (1 (1 1 1)) -1 1)))).
Il existe un ensemble de fonctions génériques dont les méthodes sont spécialisées par les classes définies précédemment. Parmi cet ensemble de fonctions génériques, nous décrirons, à titre d'exemple, un ensemble d'opérateurs rythmiques et quelques fonctionnalités Midi.
Le stage de DEA d'Olivier Delerue [Dele97] a permis d'enrichir OpenMusic d'un ensemble d'opérateurs qui réalisent des transformations complexes sur les structures musicales sans faire de concessions sur le plan temporel. Cette panoplie n'est pas exhaustive, mais elle vise à mettre en évidence un cadre général de travail sur les structures temporelles que l'on pourra éventuellement réutiliser pour la réalisation d'autres opérateurs [DeAA98].
Parmi les opérateurs réalisés, nous examinerons : les étirements temporels et la fusion de structures musicales.
- Extension / compression temporelle.
Cette opération prend en argument d'une part la structure musicale que l'on souhaite transformer et d'autre part un facteur d'étirement exprimé sous la forme d'un ratio n/p. Prenons par exemple, comme structure initiale, la voix suivante :
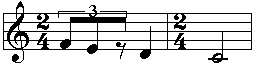
Si nous effectuons un étirement de facteur 3/2 (c'est-à-dire une extension), la croche de triolet devient une croche et la structure ternaire disparaît.
On remarquera que le résultat obtenu contient des mesures augmentées. Dans des cas plus complexes, le résultat de l'étirement n'est pas toujours facile à représenter en notation musicale.
- Fusion.
L'opérateur de fusion prend comme argument deux structures musicales et donne comme résultat une structure dans laquelle seront regroupés l'ensemble des éléments terminaux des structures initiales. Lorsque plusieurs notes interviennent simultanément, elles sont regroupées à l'intérieur d'un accord. Prenons par exemple les deux mesures suivantes :
Etant donné que cette opération n'est pas commutative il existe deux résultats possibles :
La mesure de gauche correspond au cas où le triolet est considéré comme englobant, c'est à dire que la subdivision par cinq a été propagée dans la subdivision par trois. La mesure de droite représente le cas contraire, où le quintolet est englobant.
Le traitement et le stockage d'événements Midi en OpenMusic est réalisé par MidiShare [FLOr95]. La notion non structurée d'événements Midi a été réifiée par la classe eventmidi. Cette classe hérite de la classe simple-score-element et possède trois champs : ev-type, ev-chan et ev-field.
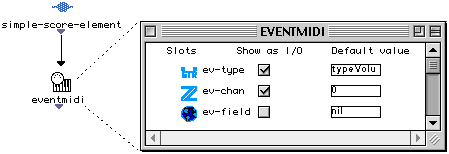
Figure 2-35 Classe eventmidi.
Le champ ev-type permet de spécifier le type d'événement Midi. MidiShare fournit une vaste gamme de types d'événements, entre autres : KeyOn, KeyOff, PitchBend, Volume, etc. Le champ ev-chan contient le numéro de canal Midi dans lequel sera envoyé l'événement. Le champ ev-field est réservé pour la liste d'arguments de l'événement.
La fonction générique MidiPlay est à la base de l'envoi d'événements Midi. La liste d'arguments de la fonction MidiPlay est donnée par (Obj ´ At ´ Approx ´ Seq) où Obj est l'objet à jouer, At le date de l'objet (en millièmes de secondes), Approx l'approximation de hauteur (demi-ton = 2, quart de ton = 4, huitième de ton = 8) et Seq est une séquence d'événements Midi que l'on remplira avec les événements nouveaux générés par Obj.
Il existe des méthodes MidiPlay spécialisées par chacune des classes musicales (Note, Chord, Voice, etc.). L'utilisateur peut réutiliser ces méthodes et en créer de nouvelles. Dans l'exemple suivant, nous créons une nouvelle classe appelée notebpf qui hérite de la classe prédéfinie note
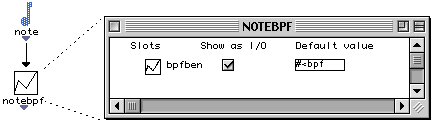
Figure 2-36 Définition d'une sous-classe de note qui joue un pitchbend.
Nous ajoutons un nouveau champ à la classe notebpf, consistant en une fonction linéaire par segments (bpf). Ce champ nous aidera à changer le comportement de la nouvelle classe par rapport à sa super-classe directe. Nous allons modifier la façon de jouer une instance de la classe notebpf. Une notebpf sera jouée comme une note standard (car la classe notebpf hérite de la classe note), mais en plus on enverra une série d'événements Midi de type pitchbend, chaque évènement étant défini par les points de la bpf.
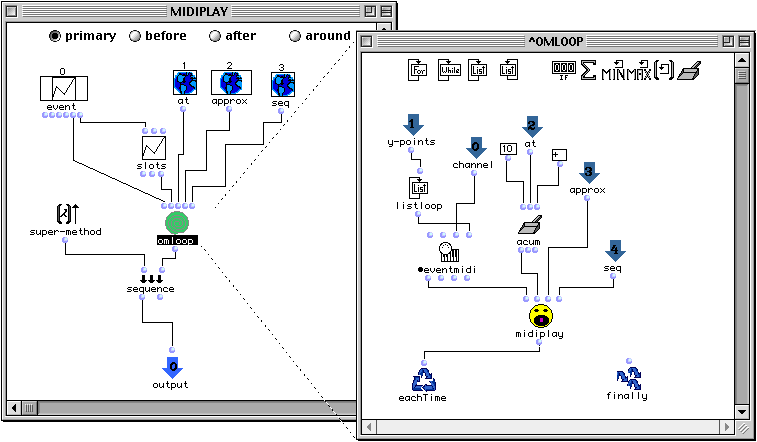
Figure 2-37 Redéfinition de la méthode MidiPlay pour une nouvelle classe.
Dans la Figure 2-37, nous avons défini la méthode MidiPlay pour la classe notebpf. La boîte super-method invoque la méthode définie pour la classe note, tandis que la boîte loop se charge de remplir la séquence avec les événements de type pitchbend. Le patch de la Figure 2-38 offre un exemple de l'utilisation de cette nouvelle classe.
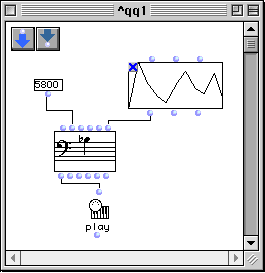
Figure 2-38 Invocation de la méthode Play pour une nouvelle classe.
De même que PW, OpenMusic associe des représentations visuelles de structures musicales complexes aux boîtes qui les calculent. La plupart des factories dont la référence est une classe musicale possèdent un éditeur en notation musicale. Les boîtes d'instance possèdent aussi un éditeur en notation musicale si leur référence est une instance d'une classe musicale avec éditeur. Nous pouvons donc déduire, qu'avoir ou pas un éditeur est une propriété d'une classe plutôt que celle d'une instance. Ainsi pour une OmClass, la gestion de l'éditeur est réalisée par l'ensemble de méthodes suivantes :
(defmethod has-editor-class-p ((self OMClass))
"Vrai si la classe possède un éditeur.")
(defmethod get-editor-class ((self OMClass))
"Retourne la classe de l'éditeur associé à la classe.")
(defmethod get-win-class ((self OMClass))
"Retourne la classe de la fenêtre où l'éditeur sera inclut.")
(defmethod get-win-ed-size ((self OMClass))
"Retourne la taille par défaut de la fenêtre de l'éditeur.")
L'évaluation d'une boîte avec éditeur, verrouillée ou en mode normal se fait de la façon expliquée dans 1.3.1.1, sauf dans le cas d'une instance, car l'évaluation d'une instance n'a pas d'effet sur l'instance (voir R2).
Les boîtes avec éditeur peuvent changer l'icône de leur cadre simple pour une visualisation simplifiée de leur éditeur (mini-vue). La Figure 2-39 montre une factory sous forme de mini-vue et son éditeur.
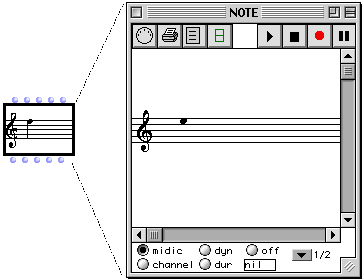
Figure 2-39 Une factory et son éditeur.
Les factories sous forme de mini-vue introduisent de l'information sémantique dans les patchs. L'icône d'une factory nous informe que cette boîte construit une instance de la classe associée à cet icône. La factory sous forme de mini-vue ne nous permet pas seulement de visualiser le type d'objet que l'on construit, mais aussi le contenu de l'objet même. Les boîtes sous forme de mini-vue à l'intérieur d'un patch offrent un mécanisme de suivi visuel de l'évaluation de chaque patch. Dans chaque mini-vue, nous visualisons l'état de certaines données à un instant de l'évaluation.
Avec l'inclusion d'une représentation graphique des instances d'une classe, OpenMusic permet l'abstraction visuelle du processus qui calcule cette instance. En plus de masquer la complexité graphique, les instances permettent de transformer un processus en un atome de calcul qui servira éventuellement de source de valeur à un autre processus.
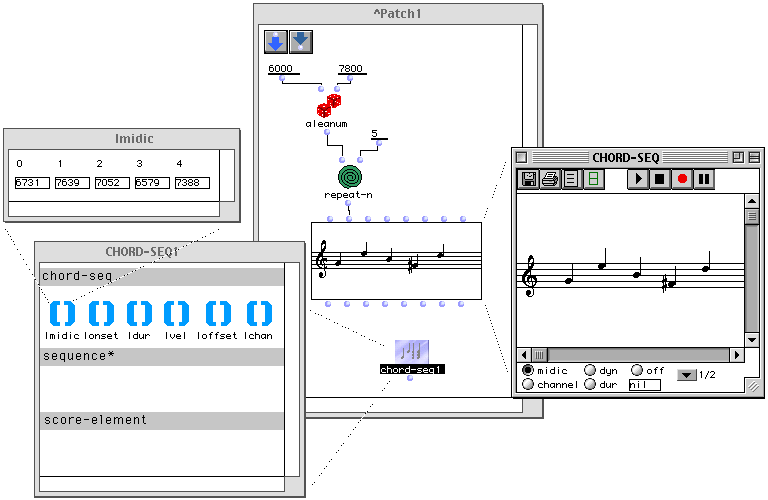
Figure 2-40 Multiple représentation d'un objet musical.
La Figure 2-40 exprime graphiquement le même objet musical sous différentes formes :
- Au niveau algorithmique, l'objet est le résultat l'opération visant à créer une séquence de 5 accords (dans notre exemple les accords ne contiennent qu'une note). L'ambitus de la note de chaque accord est défini par l'intervalle [6000 ; 7800].
- Cet objet peut aussi être vu comme une instance de la classe chord-seq où son champ Lmidic à pour valeur la liste (6731 7639 7052 6579 7388).
- Plus classiquement, l'objet est représenté par SOL MI SI FA# RE.
L'exemple d'un algorithme non déterministe souligne l'importance de pouvoir détacher un objet de l'histoire de sa construction (le patch).
Bien qu'un éditeur soit fortement lié à une instance particulière, il peut être associé à différents éléments de notre environnement, par exemple à une factory, une boîte d'instance, un item dans un projet (voir 2.2.2.1), ou un autre éditeur. En effet, la Figure 2-41 montre la possibilité d'ouvrir des éditeurs musicaux à partir de sous-objets d'un autre éditeur.
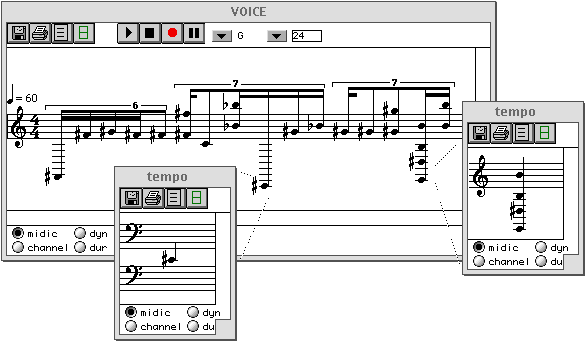
Figure 2-41 Ouverture d'éditeurs musicaux à partir d'un autre éditeur musical.
Les éditeurs sont des instances de la classe EditorView.
(defclass EditorView (OMSimpleFrame)
(object :initform nil :initarg :object :accessor object)
(ref :initform nil :initarg :ref :accessor ref)
(attached-editors :initform nil)))
(panel :initform nil :accessor panel)
(palette :initform nil :accessor palette)
(ctr-view :initform nil)))
où :
- object désigne l'objet édité (e.g. une instance de la classe note).
- ref garde l'objet auquel est associé l'éditeur (e.g. une factory).
- attached-editors contient une liste avec les éditeurs ouverts à partir de l'éditeur.
Les champs panel, palette et ctr-view sont visualisés dans la figure suivante :
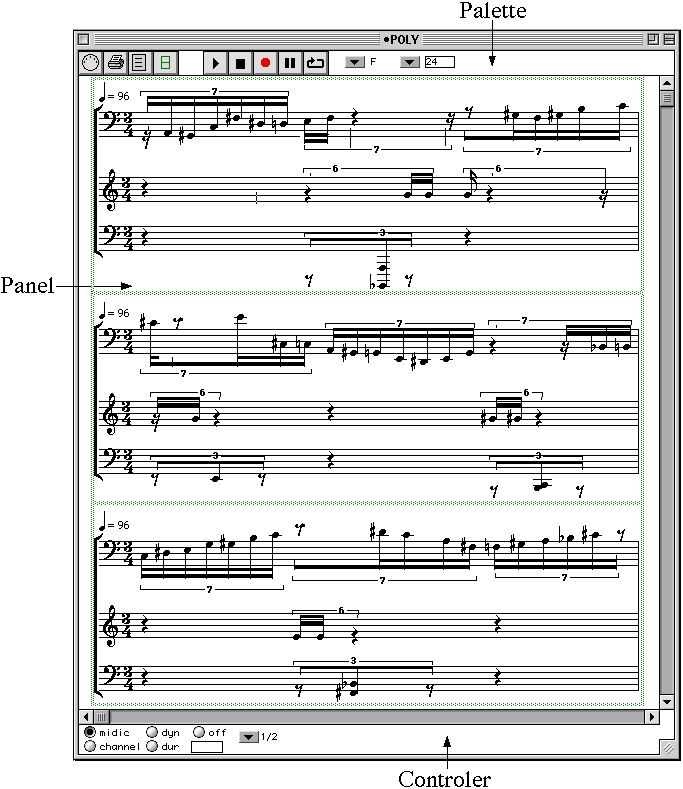
Figure 2- 42 Un éditeur rythmique.
Les éditeurs des classes voice et poly sont implémentés en utilisant CMN [Scho97].
