Aspects temporels dans OpenMusic.
Dans le chapitre 1, nous avons postulé que l'écriture musicale, et d'une façon plus générale, la notation, étaient des éléments de base spécifiques dans le rapport informatique et composition musicale [Assa93]. Dans cette thèse, nous voulons introduire un nouveau critère dans ce rapport : le temps musical, en tant que paramètre de composition. Nous commençons le chapitre 3 par exposer la représentation temporelle interne des objets musicaux. Cette représentation permet de traiter correctement les problèmes de structures temporelles discrètes et de quantification, fréquemment rencontrés dans la musique. La notion essentielle de ce chapitre est celle de maquette. Après avoir défini la notion de maquette et avoir illustré avec des exemples les divers aspects temporels de calcul et de notation présents dans les maquettes, nous finirons ce chapitre par une réflexion sur l'organisation temporelle de la grande forme (i.e. la structure globale d'une ¤uvre).
3.1 Organisation temporelle des objets musicaux.
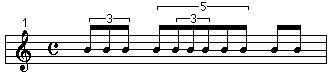
Du point de vue temporel, on est amené à faire coexister des entités qui proviennent de systèmes d'unités très différents : système d'unités plat en millièmes de secondes, par exemple pour les fichiers audio et les séquences Midi, système d'unités hiérarchiques fonctionnant sur le principe du partage d'entiers pour les structures musicales symboliques. On comprendra aisément ce dernier point à partir d'un exemple. Le fragment rythmique suivant :

peut être schématisé selon le partage d'entiers suivant, dans lequel la noire vaut 1 (u = 1) :
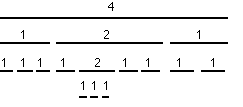
Si l'on note cette structure récursivement par :
![]()
on peut noter l'extension (durée) des composants ![]() par la formule :
par la formule :
![]()
Ainsi, la croche de triolet la plus emboîtée de notre exemple a pour extension :
![]()
Nous faisons le choix de n'utiliser que des nombres entiers pour représenter les structures temporelles emboîtées. Nous espérons, par un choix judicieux d'échelles :
Il suffit dans le dernier exemple de décider que la noire vaut 15 unités (u = 15), dans ce cas l'extension de notre croche sera 4. Mais alors elle ne sera pas commensurable avec la croche du quatrième temps qui implique u = 2. Si l'on veut rendre commensurable toutes les valeurs, il faut choisir pour l'ensemble de la mesure u = ppcm(2,3,5) = 30. Dans ce cas, les valeurs recherchées seront 8 pour la croche de triolet et 15 pour la croche du quatrième temps.
Il sera ainsi toujours possible de calculer une valeur pour u, à un certain niveau de structure, qui rende commensurables toutes les valeurs contenues dans les niveaux immédiatement inférieurs. On peut calculer la valeur de u correspondant à l'ensemble d'une partition et en déduire toutes les valeurs des structures inférieures : voix, mesures, groupes, notes. Mais on arrive très vite à de très grands nombres, gérables dans certains environnements (e.g. BigNums en Common Lisp), mais qui posent tout de même des problèmes de mémoire et d'efficacité. De surcroît, cette complexité n'est pas nécessaire à tous les niveaux : si l'on extrait une sous-structure (e.g. une mesure) d'une sur-structure (e.g. une voix) pour lui appliquer un opérateur (e.g. la jouer), une valeur de u locale, nécessaire et suffisante compte tenu de la complexité interne de la sous-structure, doit faire l'affaire. D'où l'idée d'un système d'échelles variables, toujours en nombres entiers, adapté à chaque niveau d'emboîtement des structures musicales.
Cette organisation est schématisée dans la Figure 3-1.
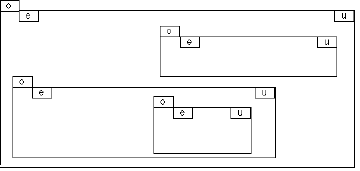
Figure 3-1 Organisation temporelle des instances musicales.
Chaque conteneur possède trois attributs entiers :
- u qui définit l'échelle pour ce conteneur.
- o est l'offset de ce conteneur, exprimé par rapport à l'attribut u du conteneur immédiatement englobant. o est égal à 0 s'il n'y a pas de conteneur englobant.
- e est l'extension de ce conteneur exprimée par rapport à l'attribut u appartenant à ce même conteneur.
Dans OpenMusic, toute structure musicale est un conteneur qui renferme d'autres structures musicales. Tout conteneur a une extension temporelle (e) et un temps de début ou offset (o) relatif à son contenant. o et e sont des entiers qui s'expriment dans une échelle dont l'unité est une fraction 1/u de la noire, où u est un entier redéfinissable à chaque niveau d'emboîtement.
Les primitives de manipulation de base des structures musicales sont les suivantes :
- NewContainer
NewContainer crée un container vide. u = 1 par défaut.
- AddTo container1 container2 at
Cette opération place le container2 dans le container1 à la position at. at est exprimée dans une unité définie comme une fraction de noire.
u = u(container1)
p = ppcm(u, dénominateur(at))
u(container1)= p
o(container2) = at * p
o(![]() ) =
o(
) =
o(![]() ) * p / u pour tout
) * p / u pour tout ![]() sous-conteneur immédiat de
container1
sous-conteneur immédiat de
container1
Insérer container2 dans container1.
- RemoveFrom container1 container2
o(container2) = 0
Libère le container2 du container1.
- QReduce container [n]
Qreduce calcule
u' = ppcm ( u(![]() ) ) où
) ) où ![]() parcourt tout l'arbre des conteneurs dont container est la
racine. Il effectue ensuite u(
parcourt tout l'arbre des conteneurs dont container est la
racine. Il effectue ensuite u(![]() ) =
u' puis change corrélativement les o(
) =
u' puis change corrélativement les o(![]() ) et les e(
) et les e(![]() ). Qreduce rend donc toutes les
parties de container commensurables. Si n est
spécifié, u' = ppcm(u(
). Qreduce rend donc toutes les
parties de container commensurables. Si n est
spécifié, u' = ppcm(u(![]() ), n)
), n)
- QNormalize container
Cette fonction est symétrique de Qreduce. Elle affecte
à chaque ![]() de l'arbre un
u nécessaire et suffisant grâce à un
calcul de pgcd sur les parties immédiates de
de l'arbre un
u nécessaire et suffisant grâce à un
calcul de pgcd sur les parties immédiates de ![]() . QNormalize change
corrélativement les o(
. QNormalize change
corrélativement les o(![]() ) et
les e(
) et
les e(![]() ).
).
Ainsi, pour ramener à la même échelle deux structures c et c' aux fins de les comparer, de les fusionner, etc., la séquence des opérations sera la suivante :
c'' = NewContainer ()
AddTo (c'', c, 0)
AddTo(c'', c', 0)
QReduce (c'')
RemoveFrom(c'', c)
RemoveFrom(c'', c')
Le modèle présenté ici s'applique naturellement aux structures musicales symboliques dans lesquelles les catégories traditionnelles de polyphonie, voix, mesures, groupes, sous-groupes, valeurs (container terminaux) sont aisément représentées comme des sous-classes de la classe container. Mais, il nous sert aussi à faire le lien, au sein des maquettes (voir 3.2), entre ces structures symboliques et des objets hétérogènes comme les séquences audio ou Midi, et les scripts de synthèse. Par exemple, si l'on voulait placer dans le même conteneur une séquence audio S, au temps 1.3 secondes, et une structure symbolique S' au temps 4 secondes (avec une noire par défaut à 60), la séquence des opérations serait la suivante :
c = NewContainer ()
AddTo (c, S', 4)
AddTo(c, S, 1300/1000)
La lecture des valeurs après installation donnerait :
u(c) = 10, o(S') = 40, o(S) = 13
Si l'on voulait en extraire une partition mixte avec une impulsion de noire à 60, il serait facile de calculer que la séquence audio commence sur une seconde croche de triolet du deuxième temps et la séquence symbolique sur le quatrième temps.
Nous définissons les deux classes CLOS suivantes qui implémentent la notion de conteneur par :
(defclass simple-container ()
((parent :initform nil)
(Qvalue :initform 1)
(Qtempo :initform 60)
(offset :initform 0)
(extent :initform 1)))
(defclass container (simple-container)
((inside :initform nil)))
Pour la classe simple-container :
La classe container est une sous-classe de simple-container , cette classe regroupe les objets qui peuvent renfermer d'autres conteneurs. Le champ inside garde la liste des conteneurs de l'objet.
La représentation interne des objets musicaux dans OpenMusic (instances des classes définies dans 2.2.3.1) est basée sur la notion de conteneur. Afin de faire le lien entre les classes CLOS : container et simple-container , et les classes musicales dans OpenMusic, nous définissons une série de classes abstraites dans OpenMusic, mais qui héritent des classes CLOS. Le package music-expert définit cet ensemble de classes abstraites.
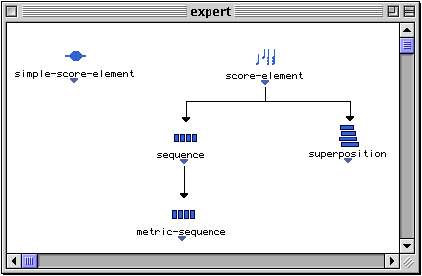
Figure 3-2 Classes abstraites pour l'interface entre conteneurs et classes musicales.
Les classes simple-score-element et score-element héritent respectivement de la classe simple-container et container. La classe sequence définit un conteneur dont les éléments sont disposés les uns après les autres, tandis que la classe superposition dispose ses éléments en parallèle. Une dernière classe abstraite, metric-sequence, implémente des séquences rythmiques.
Les maquettes ouvrent un espace récursif dans lequel s'articulent en largeur, en hauteur et en profondeur des structures musicales qui peuvent être : des séquences Midi, des fichiers audio, des scripts de synthèse, des structures musicales notables sous la forme de partitions, ou des patchs qui calculent les objets précédents. Les patchs peuvent contenir des maquettes et les maquettes peuvent à leur tour figurer dans un patch en tant que sources de valeur.
La caractéristique primordiale d'une maquette provient de la possibilité de combiner calculs et représentations dans un même objet.
- En ce qui concerne le calcul, une maquette peut être vue comme un patch contenant des boîtes spéciales appelées boîtes temporelles, qui éventuellement peuvent communiquer entre elles à l'aide de connexions. Mais à la différence d'un patch, dans une maquette certaines propriétés des boîtes temporelles, comme la position ou la taille, entre autres, peuvent jouer un rôle déterminant dans l'évaluation.
- Parallèlement, on peut concevoir une maquette comme un conteneur (dans le sens défini dans 3.1) renfermant d'autres conteneurs résultant de l'évaluation des boîtes temporelles.
La vue d'une maquette est définie par le cadre simple :
L'éditeur d'une maquette ressemble à l'éditeur d'un patch, mais en plus l'axe horizontal est muni d'une "règle temporelle", ayant pour unité la seconde et comme subdivision maximale la millième de seconde. Cette règle sert de référence à la définition de la position et de la durée des boîtes temporelles.
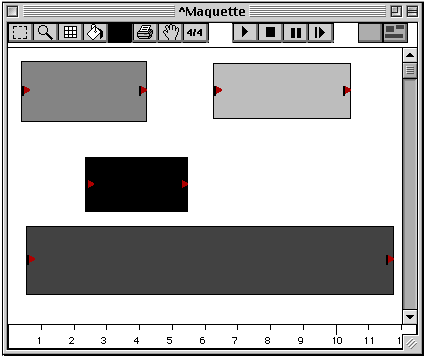
Figure 3-3 Une maquette sous forme de container.
Les boîtes temporelles comme les boîtes classiques (voir chapitre 2) possèdent une valeur et une référence. La valeur d'une boîte temporelle peut être ou non une valeur temporelle. Dans le deuxième cas, la boîte n'est pas prise en compte pour la construction du conteneur qui sera le résultat de la maquette. Il existe trois types de références pour une boîte temporelle :
La Figure 3-4 nous montre la hiérarchie de classes des objets participant à l'implémentation des maquettes. Les classes OMPatch et OMBox ont été définies dans 2.2.1.7.
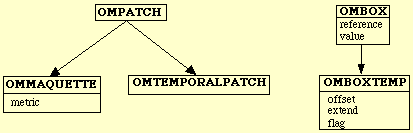
Figure 3-4 Hiérarchie de classes pour l'implémentation des maquettes.
Le champ boxes (que la classe OMMaquette a hérité de la classe OMPatch ) contient une liste d'instances de la classe OMBoxTemp. La gestion des événements de même que la représentation graphique se font en suivant le paradigme décrit dans le chapitre 2.
Un nouveau champ, metric, est ajouté à la classe OMMaquette. Ce champ contient une information relative au tempo, à la métrique, et à la subdivision minimale, permettant éventuellement à la maquette de se comporter comme une metric-sequence (voir 3.1.1).
La classe OMTemporalPatch possède la même structure que la classe OMPatch. La différence apparaît au niveau du comportement, plus particulièrement dans la méthode qui compile en Lisp l'algorithme défini par le patch. La classe des boîtes temporelles OMBoxTemp est aussi un méta-objet d'OpenMusic, ce qui offre des possibilités intéressantes que nous exposerons plus loin.
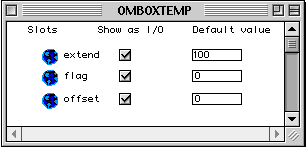
Figure 3-5 Structure de la classe OMBoxTemp.
La Figure 3-5 montre la classe OMBoxTemp sous forme de container.
Il existe aussi un protocole (i.e. un ensemble de fonctions génériques) qui permet à l'utilisateur de modifier le comportement et la structure des boîtes temporelles par les mécanismes de sous-classage et de redéfinition. Ce protocole est défini principalement par les fonctions :
(defmethod* starttime ((self omboxtemp) &optional (val nil))
"Pour la lecture et l'écriture du champ offset")
(defmethod* objdur ((self omboxtemp) &optional (val nil))
"Pour la lecture et l'écriture du champ extend")
(defmethod* mymaquette ((self omboxtemp))
"Retourne la maquette contenant self")
(defmethod* put-in-maq ((self omboxtemp) (maquette ommaquette))
"Inclue la boîte temporelle self dans la maquette maquette")
(defmethod* objflag ((self omboxtemp) &optional control)
"Pour la lecture et l'écriture du champ flag"))
(defmethod* eval-tempobj ((self omboxtemp))
"Evalue la boîte temporelle self")
Un Patch Temporel est un patch classique muni d'une sortie et d'une entrée, par défaut. La sortie appelée tempout (Figure 3-6) est chargée de déterminer le résultat de l'évaluation qui correspondra au champ value de la boîte temporelle dont le patch est la référence. L'entrée self est un représentant de classe de la classe OMBoxTemp qui sera remplacée à chaque évaluation par la boîte elle même.
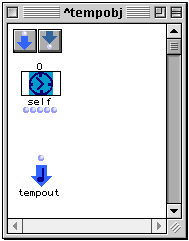
Si un patch classique peut être vu comme une fonction, par contre, un patch temporel définit une méthode spécialisée par la classe OMBoxTemp, et éventuellement un nombre illimité de paramètres de type universel.
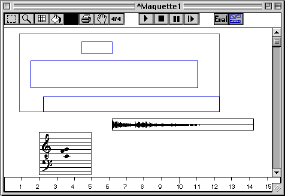
Figure 3-7 Une maquette avec les trois types de boîtes temporelles.
La Figure 3-7 montre un exemple d'une maquette contenant des boîtes temporelles avec les trois types de références mentionnées. En allant de haut en bas, la première boîte a pour référence une maquette qui contient 3 boîtes temporelles, la deuxième boîte a pour référence une instance de la classe sound, la dernière boîte présente un accord qui a été calculé par le patch temporel suivant.
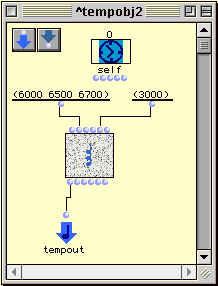
Figure 3-8 Un patch temporel calculant un accord.
Le patch de la Figure 3-8 est un exemple simple de la façon dont on peut construire des valeurs pour les boîtes temporelles. Ce patch en particulier, n'utilise pas l'entrée self. Le patch suivant illustre de façon didactique les possibilités offertes en utilisant une telle entrée.
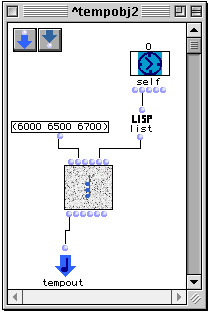
Figure 3-9 Un patch temporel qui utilise son entrée self.
Dans la Figure 3-9 le patch montré dans la Figure 3-8 a été modifié par la spécification de la durée de l'accord en proportion directe avec le temps d'attaque de la boîte temporelle. Ainsi l'évaluation de la boîte lors des différentes positions produira des résultats différents (Figure 3-10).

Figure 3-10 Trois évaluations d'une même boîte temporelle avec différents résultats.
Il existe deux opérations principales pouvant s'effectuer sur une boîte temporelle qui ne sont pas liées à l'évaluation : le déplacement et le changement de la durée Les méthodes correspondant à ces opérations pour la classe OMBoxTemp sont définies de la manière suivante :
(defmethod* OM-Move-Object ((self omboxtemp) new-position)
(defmethod* OM-Change-Size ((self omboxtemp) new-size)
Cependant ces deux méthodes peuvent être définies différemment pour toute sous-classe de OMBoxTemp. Ce type de modification peut introduire des incohérences entre la valeur de l'évaluation d'une boîte et son état après modification (particulièrement dans le cas où l'algorithme calculant la valeur de la boîte prend comme paramètre la position ou la durée de la boîte). Cela demande l'introduction d'une convention pour la représentation des boîtes, cette convention est illustrée dans le graphique suivant.
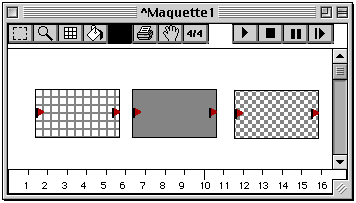
Figure 3-11 Convention pour la représentation des boîtes temporelles par rapport à leur valeur.
Il existe trois types de visualisation pour une boîte. Dans la Figure 3-11, de gauche à droite :
- On voit d'abord une boîte dont la valeur n'est pas un objet temporel.
- Au milieu, on observe une boîte avec une valeur qui est un objet temporel. La durée et la position de cette boîte n'ont pas changé depuis l'évaluation qui a produit sa valeur. Nous dirons que cette boîte est "cohérente" avec sa valeur.
- Le dernier type de visualisation indique que la boîte a une valeur qui est un objet temporel, mais qu'elle a subi des modifications après son évaluation. Il est donc possible que sa valeur ne corresponde pas au calcul du patch temporel dans le contexte actuel.
En dehors de ces types de représentations de base, l'utilisateur peut rendre plus expressives ses maquettes, en utilisant des visualisateurs prédéfinis par les instances de classes musicales (e.g. Figure 3-10), ou en associant aux boîtes des images qui décrivent l'aspect sémantique de la boîte. La maquette suivante, extraite d'une pièce pour piano du compositeur Mikhail Malt, est un bon exemple de cette dernière option.
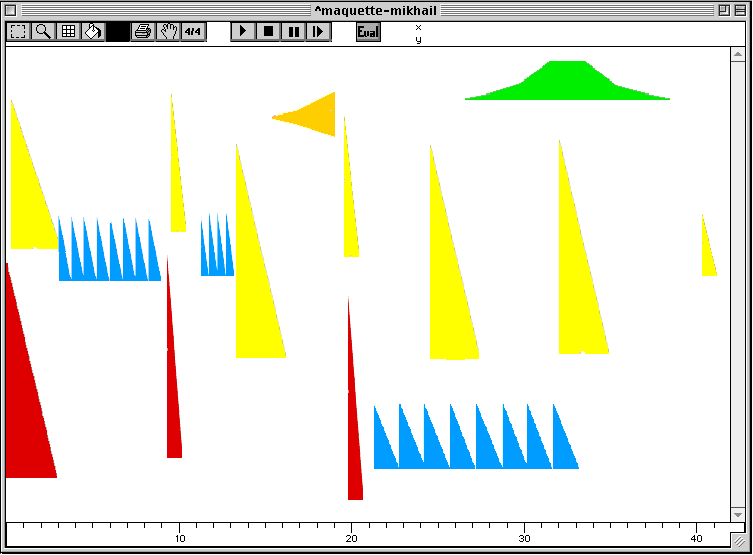
Figure 3-12 Une maquette du compositeur Mikhail Malt.
Comme un patch classique, un patch temporel peut posséder de multiples absins et absouts, en dehors des entrées/sorties spéciales déjà mentionnées. L'ajout d'absins et d'absouts dans un patch temporel s'exprime dans la boîte temporelle par l'ajout de paramètres d'entrée et de sortie. Ces paramètres permettent le passage des valeurs (en temps d'évaluation) entre les différentes boîtes temporelles à l'aide de connexions.
Figure 3-13 Deux patchs temporels qui communiquent entre eux.
Prenons par exemple le patch de la Figure 3-9 et ajoutons une sortie à laquelle on connecte la sortie des hauteurs de l'accord (Figure 3-13 (a)) et construisons une nouvelle boîte ayant pour référence le patch qui à son tour possédera une entrée sur laquelle on fera une opération de transposition et de renversement pour construire une séquence d'accords (Figure 3-13 (b)).
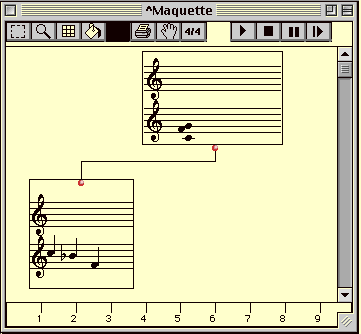
Figure 3-14 Dualité entre temps d'évaluation et temps dans la maquette.
La maquette précédente montre le résultat d'une évaluation dans laquelle la sortie de la boîte qui génère l'accord (boîte A) a été connectée à l'entrée de la boîte qui construit la séquence (boîte B). Pour cet exemple, il faut noter la dualité entre le temps de calcul et le temps défini par la règle de la maquette. En effet, la boîte A se trouve après la boîte B selon la règle temporelle. Cependant, en temps d'évaluation, la boîte A doit être évaluée en première instance afin de produire la valeur qui servira d'entrée pour l'évaluation de la boîte B. Ce fait, pouvant perturber les amateurs du temps réel, est considéré comme l'une des caractéristiques principales de notre modèle.
La construction d'une maquette se fait généralement à l'aide du mécanisme de glisser-déposer où l'utilisateur dépose la référence d'une nouvelle boîte temporelle sur une position donnée dans la maquette. Il est aussi intéressant d'offrir la possibilité de créer une maquette de façon algorithmique. Nous avons vu dans 2.2.2.3. que les différents éléments de base de notre langage (i.e. patchs, maquettes, boîtes, etc.) ont été implémentés sous forme de meta-objets. Cela nous permet d'inclure à l'intérieur d'un patch des factories ayant pour référence les classes des méta-objets.
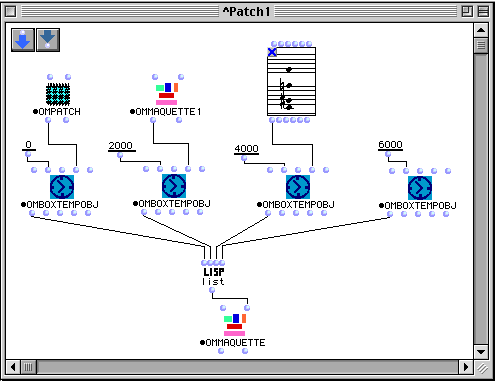
Figure 3-15 Construction algorithmique d'une maquette (première version).
L'exemple de la Figure 3-15 montre la construction d'une maquette contenant quatre boîtes temporelles ayant comme onset 0, 2, 4 et 6 secondes. Chacune prend respectivement comme référence un patch, une maquette, un accord et rien. Dans le dernier cas, un patch temporel par défaut servira de référence à la boîte.
L'exemple suivant (l'algorithme principal est expliqué dans l'annexe II.4.) montre un algorithme qui construit des emboîtements de maquettes à partir d'une liste. Ce patch illustre l'intérêt de construire des maquettes de façon algorithmique. Le principe est le suivant : à partir d'une liste donnée, (((2 1)(2 2))((1 1)(1 2))) par exemple, le patch construit une maquette pour chaque niveau de parenthèses. Cette maquette contient des boîtes temporelles ayant pour référence d'autres maquettes et ainsi de suite jusqu'au moment où on trouve un terminal (un entier). À ce moment-là, on construit une boîte produisant un accord dont la durée est spécifiée par la valeur du terminal (en secondes). Pour la liste de notre exemple, la maquette créée est montrée dans la Figure 3-16.
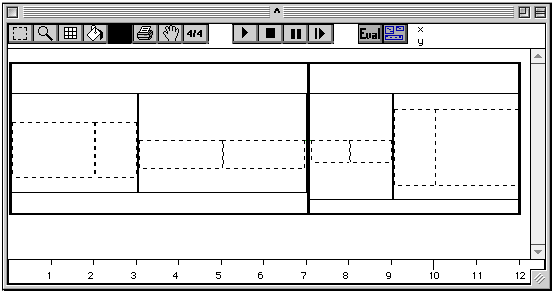
Figure 3-16 Un ensemble de maquettes emboîtées.
Nous croyons cependant, que cette façon de construire des maquettes demande une connaissance informatique avancée. C'est pour cette raison que nous introduisons un nouveau type de boîte que nous appellerons boîte de maquette.
-Vue

-container

Une boîte de maquette a la même structure qu'une boîte classique, mais sa référence est restreinte aux maquettes, et sa valeur sera toujours une instance de la classe superposition (voir 3.1.1). Le premier paramètre d'entrée dans une boîte de maquette fournit une liste d'onset tandis que le deuxième une liste de références. L'évaluation d'une boîte de maquette permet de construire et d'ajouter à la maquette, un ensemble de nouvelles boîtes temporelles ayant pour références les objets spécifiés par le deuxième paramètre et positionnées par rapport aux temps donnés par la première entrée. Le résultat d'une telle évaluation produit une instance de la classe superposition, construite par rapport aux boîtes temporelles.
Nous introduisons aussi un nouveau visualisateur d'état représenté par "flêche", qui pour toute boîte produit la règle d'évaluation suivante (R15) :
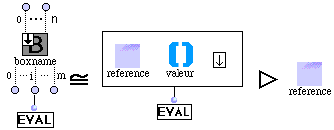
Ainsi, le patch de la Figure 3-15 peut être simplifié de la façon suivante :
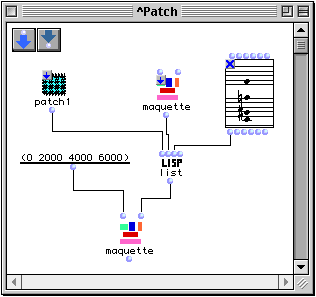
Figure 3-17 Construction algorithmique d'une maquette (simplification).
Nous avons vu dans la Figure 3-13 comment deux ou plusieurs boîtes peuvent s'envoyer des données à l'aide de connexions. Nous incrémentons le pouvoir d'expression d'une maquette grâce à la possibilité qu'ont les boîtes temporelles d'avoir accès aux autres boîtes temporelles appartenant à la maquette. Cette possibilité nous permet d'avoir un ordre d'évaluation qui ne dépend pas uniquement du graphe des connexions, mais éventuellement des caractéristiques de chacune des boîtes constituant la maquette. L'exemple suivant (Figure 3-18) montre une maquette constituée des trois boîtes temporelles.
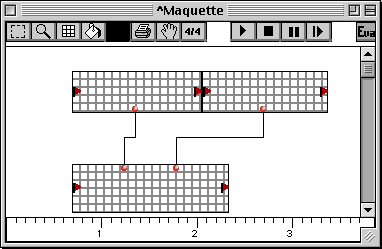
Figure 3-18 L'évaluation d'un boîte temporelle modifie la position d'autres boîtes dans la maquette.
Les deux premières boîtes, situées en haut de la maquette, ont pour référence le patch suivant :
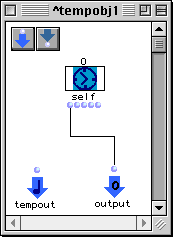
Figure 3-19 Un patch temporel exportant la boîte temporelle dont il est la référence.
Indépendamment de l'objet temporel fourni par les deux boîtes, la boîte restante joue un rôle passif (sa valeur ne fait pas partie de l'objet résultant de la maquette). Cependant, cette dernière boîte nous permet d'organiser les deux autres, car toutes deux sont passées comme paramètres. L'algorithme qui implémente la troisième boîte est donné par le patch de la Figure 3-20.
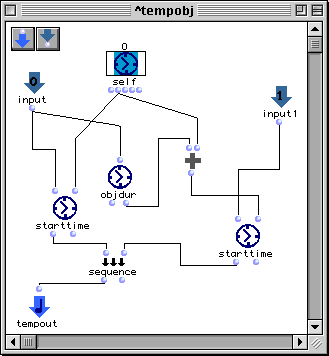
Figure 3-20 Un patch temporel contrôlant d'autres boîtes dans une maquette.
Ainsi, une évaluation de la maquette, quelle que soit la position des boîtes, ramènera les deux boîtes, l'une après l'autre à la même position que la troisième boîte.
Un dernier exemple montre la possibilité de créer dynamiquement en temps d'évaluation de nouvelles boîtes et de modifier l'ordre d'évaluation. Pour cela, nous supposons l'existence d'un patch (voir Annexe II.5.) qui clone une boîte temporelle tout en incrémentant d'une unité son champ flag qui commence avec la valeur 0.
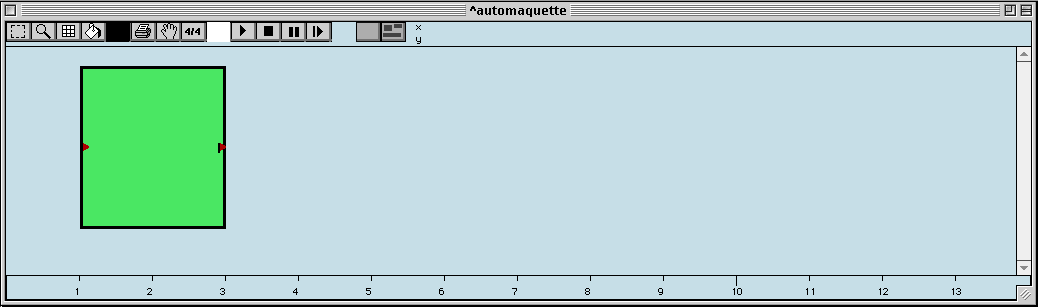
Figure 3-21 Un clonage en chaîne d'une boîte temporelle.
La Figure 3-21 montre une maquette ayant pour unique élément une boîte temporelle dont la valeur est calculée par le patch suivant :
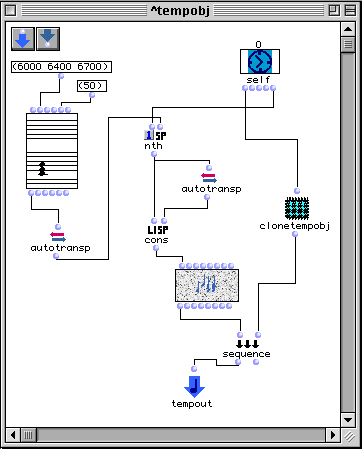
Figure 3-22 Un patch temporel qui clone la boîte dont il est la référence.
Le patch temporel de la Figure 3-22 est divisé en deux opérations :
- D'abord, il construit une séquence d'accords à partir d'un accord de base. La boîte autotransp prend comme entrée un accord et construit une séquence dont chaque accord est une transposition de l'accord original, ayant au moins une note qui garde la même hauteur. Le patch prend le ième élément de la séquence d'auto-transpositions et applique l'algorithme d'auto-transposition pour cet accord. La valeur i est donnée par la valeur du champ flag de l'entrée self.
- Puis, une copie de la boîte temporelle est construite à l'aide du patch nommé clonetempobj (voir Annexe II.7), celui-ci incrémente de 1 la valeur du champ flag de la nouvelle copie. Cette nouvelle copie est aussi insérée dans la maquette et évaluée, donc tout le processus est répété n fois (n est spécifié dans le patch clonetempobj, dans notre exemple n = 5). L'évaluation de la maquette est montrée dans la Figure 3-23.
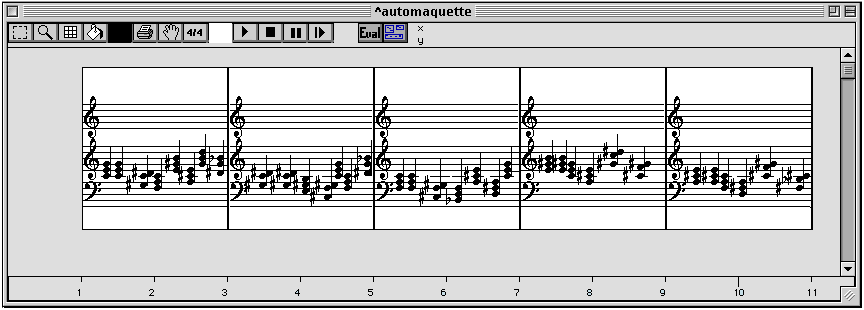
Figure 3-23 Une séquence d'accords auto-transposés.
Dans les maquettes, les structures d'imbrication hiérarchique et d'ordonnancement temporel, en d'autres termes, la forme, disposent d'une représentation visuelle explicite. L'esquisse pour piano de la Figure 3-12, contient un certain nombre de boîtes temporelles. Leur position correspond à des dates en temps absolu. Leur extension horizontale correspond à leur durée. Leur extension verticale figure l'intensité. Des dessins ont été superposés à ces blocs dans un but de sémiotique musicale élémentaire. Ainsi, les triangles correspondent à des accords frappés dont la résonance décroît rapidement. Les figures en dent-de-scie sont des ostinato d'accords. Le triangle couché et la forme en cloche sont des trilles rapides dont l'intensité croît ou décroît continûment en suivant la géométrie indiquée.
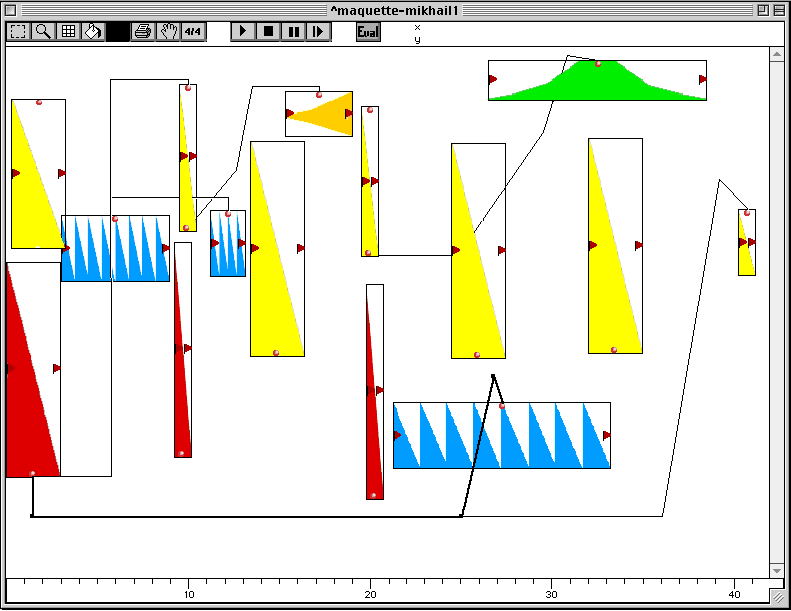
Figure 3-24 Le niveau d'organisation dynamique.
Dans la Figure 3-24, les connexions entre boîtes temporelles ont été révélées. Elles sont porteuses d'un autre niveau de sémantique musicale. On peut en effet y voir que les blocs se déduisent les uns des autres par des relations fonctionnelles. Ainsi, le troisième ostinato est-il relié au premier accord.
Si l'on "ouvre" cet ostinato (Figure 3-25) on accède à un troisième niveau de l'organisation musicale, qu'on pourrait qualifier de syntaxique : c'est en effet ici que des éléments de matériau vont devenir des syntagmes par déploiement horizontal. On peut aisément comprendre que l'accord qui entre dans ce patch par la flèche labellisée input se voit transposé d'une quarte augmentée redoublée (18 demi-tons soit 1800 cents), puis répété 6 fois, et envoyé dans un module de construction de séquence d'accords.
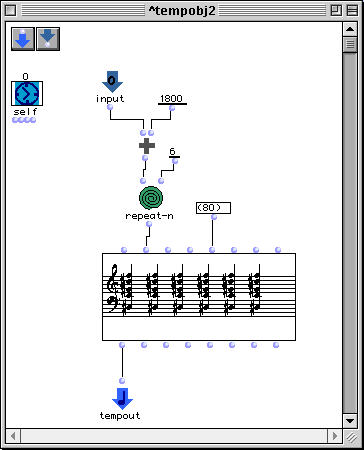
Figure 3-25 Le niveau d'organisation syntaxique.
Revenons au premier accord en bas à gauche qui se fournit lui-même comme matériau à l'ostinato décrit au paragraphe précédent et ouvrons le (Figure 3-26). Ici l'algorithmique de construction est réduite à sa plus simple expression puisqu'on n'y trouve que la définition littérale d'un accord, entré à la main par le compositeur. Nous sommes donc au quatrième et dernier niveau, celui du matériau brut.
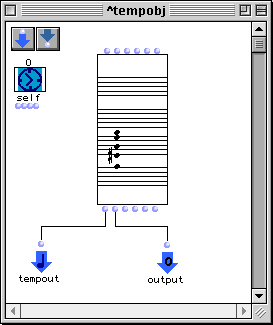
Figure 3-26 Le niveau d'organisation du matériau dans.
Pour terminer, changeons la nature de l'affichage en imposant, la notation musicale traditionnelle (Figure 3-27).
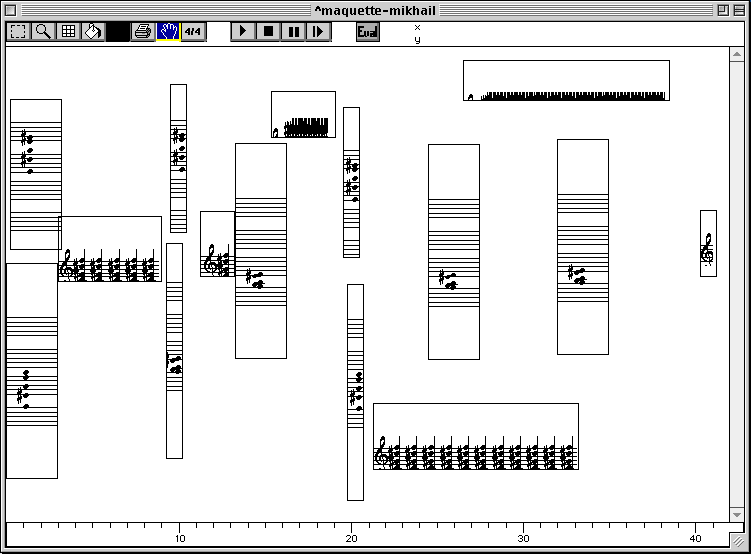
Figure 3-27 Boîtes temporelles sous forme de mini-vues.
Devant cet outil complètement nouveau qu'est la maquette d'OpenMusic, nous avons donc accès de manière fluide à quatre niveaux interdépendants d'organisation musicale :
Ces quatre axes d'organisation sont autant de logiques musicales qui s'interpénètrent, l'innovation majeure étant ici de matérialiser cette interpénétration en d'en donner un contrôle interactif au compositeur. Ce contrôle débouche sur des possibilités d'expérimentations combinatoire inédites :
Ces quatre modalités expérimentales peuvent évidemment être combinées entre elles.
3.2.2 Maquettes et organisation temporelle.
La grande forme dont nous parlons dans la section précédente est le résultat de la mise en relation (par un compositeur) d'un certain matériau. Nous pouvons faire correspondre le matériau avec les blocs à l'intérieur de la maquette, cette dernière étant l'outil principal de mise en relation. Cette division entre matériau et organisation est connue mais n'est pas assez explicative, en effet il n'existe pas d'objets musicaux sans relations, ni de relations en dehors des objets. Un matériau compositionnel est organisé (voir 3.1), de même une organisation peut aussi servir de matériau (voir 3.2). Nous considérons un objet musical comme une relation d'objets musicaux avec la possibilité d'une mise en relation avec d'autres objets musicaux. En résumé, un objet musical est identifié comme tel dans la mesure où le compositeur décide qu'il soit un objet musical. Cette définition, peu formelle, n'est pas en désaccord avec les structures de données définies dans 3.1, ni avec la notion de maquette. En rejetant la définition d'un objet musical insécable et immobile, nous adhérons aux notions de " champ de forces " et " action sonore ". La notion d'objet musical telle qu'on l'a présentée ne nous empêche pas de définir de multiples relations à l'intérieur d'une pièce, elle n'interdit pas non plus l'appartenance possible d'un même objet à diverses relations.
Dans les maquettes, nous relevons deux relations principales : une relation de causalité et une relation temporelle. La causalité entre deux boîtes sera définie par rapport au "temps d'évaluation". L'évaluation d'une maquette suit le même paradigme que pour les patchs. Comme ce type d'évaluation est très simple (nous n'avons pas d'évaluations en parallèle), il permet de mettre en relation les boîtes par un ordre strict. De même, la règle de la maquette permet de comparer les objets temporels par rapport à leur "temps physique". Afin de mieux comprendre la façon dont une maquette peut représenter simultanément ces deux ordres, prenons l'exemple suivant :
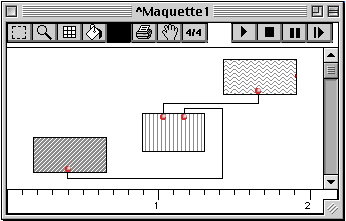
Figure 3-28 Ordre causal et ordre temporel dans une maquette.
Les deux graphiques suivants expliquent comment peuvent s'ordonner différemment les boîtes par rapport au temps physique ou de calcul, pour la maquette de la Figure 3-28.


L'intérêt de la maquette ne se limite pas à la simple représentation des deux relations exposées, mais elle s'étend à la combinaison des deux.
Avec la possibilité d'emboîter des maquettes, nous découvrons un nouveau paradoxe : prenons par exemple la maquette de la Figure 3-29.
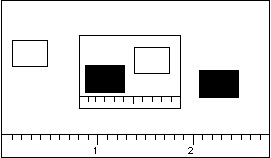
Figure 3-29 Deux objets appartenant à deux relations temporelles différentes.
Si la boîte noire (BN) et la boîte blanche (BB)
représentent les mêmes objets, alors nous pouvons dire
que ![]() mais aussi que
mais aussi que![]() .
.
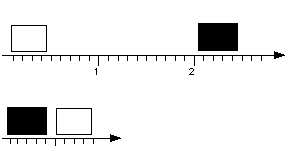
Selon nous, l'existence de plusieurs "règles temporelles" dans une maquette implique l'existence de plusieurs relations dans une même maquette. Dans une composition musicale, l'organisation du matériau n'obéit pas forcément à ces deux relations. Le matériau peut suivre d'autres ordres imposés arbitrairement par le compositeur, ainsi, la figure suivante montre une séquence autrement "ordonnée" de notes.
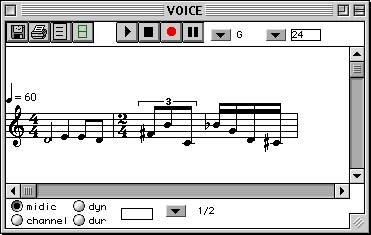
Étant donné la diversité de relations à l'intérieur d'une pièce, un même objet peut appartenir à différentes relations. Voici comment, l'exemple de la figure précédente a été enrichi d'une nouvelle relation.
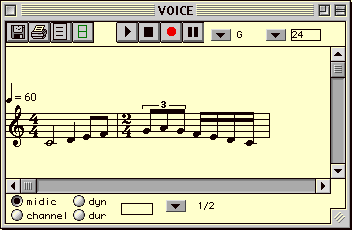
L'enrichissement des maquettes par la visualisation et la combinaison de n'importe quel type de relation définie par le compositeur nous permettra d'explorer de nouveaux domaines concernant le temps musical pour la CAO. Cependant, il est prématuré de parler de temps musical, nous sommes conscients qu'il faut commencer par une définition ou au moins par la proposition d'une notion de temps musical qui rendrait compte des différentes propriétés du temps musical. Mais un discours musicologique est insuffisant pour la conception d'outils informatiques de composition. Nous devons aussi examiner les divers travaux sur les représentations et les raisonnements temporels afin de définir de manière formelle le modèle temporel que nous allons adopter. L'établissement d'un vocabulaire concernant les concepts de relation, d'ordre, de linéarité, etc. nous semble aussi fondamental.
Les lignes finissant ce chapitre montrent l'état actuel de nos recherches sur le temps musical.
Personne ne met en doute le caractère temporel de la musique, il existe un consensus sur la nécessité d'un temps physique pour le déroulement de la musique. Au contraire, l'expression "temps musical" a divisé les esthéticiens et les musiciens de ce siècle entre ceux qui nient son existence et ceux qui non seulement l'acceptent, mais placent le temps musical au c¤ur de la musique. Notre conception du temps musical est proche de celle de Francis Courtot : "...le temps dans la musique est différent du temps physique et philosophique. Le temps musical est plutôt en relation à la forme musicale qu'à un concept homogène et continu. ".[Cour90]
Vers la fin du XIXème siècle, le temps commence à être considéré comme un paramètre de composition au même titre que la hauteur ou le rythme. C'est vers cette époque que l'expression "temps musical" fait son apparition, Ch. Koechlin est le premier à l'utiliser ; pour lui le temps musical est le résultat d'une organisation d'événements. L'argument qui permet d'établir l'autonomie du temps musical est l'impossibilité de réduire l'activité temporelle de la musique à une autre activité, que cette dernière soit gouvernée par le temps physique, psychologique ou philosophique. Cette impossibilité de réduction n'implique pourtant pas la non-relation entre ces divers temps ; le temps musical a des propriétés quantitatives et qualitatives, sans avoir une position extrême. Cette vision du temps musical comme résultat d'une organisation est décourageante à cause de la quantité de paramètres qui doivent être pris en compte, mais aussi à cause du caractère subjectif qu'elle impose. L'inclusion d'un "organisateur" du temps musical nous empêche de définir, pour une pièce, un énoncé axiomatique ; dans ce sens nous ne croyons pas à l'existence d'un temps musical. Toutefois, il serait triste de finir notre travail ainsi. La construction individuelle d'un temps par chaque auditeur nous semble une bonne idée pour continuer notre recherche, cependant la question suivante semble logiquement s'imposer : si le temps musical est propre à chaque individu comment peut-il être partagé par diverses personnes ? L'approche de G. Brelet semble bien convenir à notre domaine : Brelet voit dans le temps musical, l'essence métaphysique du temps. Le temps musical passe par les formes sonores, rythmiques et musicales. Ce sont les ¤uvres elles mêmes qui engendrent le temps musical, ce dernier est inséparable du matériau et de l'organisation de la pièce, bref il s'agit ici d'une métaphysique immanente de la musique. Voici donc une première prise de position : la pièce musicale est porteuse d'informations temporelles, sans cette affirmation, on imagine mal comment on pourrait utiliser la CAO en ce qui concerne le temps. Le statut du temps musical en tant que paramètre de composition, implique non seulement son éventuelle manipulation (i.e. inversion), mais aussi la possibilité de le définir comme le résultat d'un calcul.
À l'intérieur de l'activité musicale, nous sommes confrontés à une multiplicité de temps. En ce qui concerne le temps musical, nous parlons de compositeur, d'interprète et d'auditeur pour désigner tout être qui participe, chacun à sa manière, au déploiement de la musique. Bien sûr, une telle division est démunie de sens si on l'interprète comme une partition. Comment imaginer un interprète qui ne soit à la fois compositeur et auditeur ? Ou comment concevoir une expression artistique où la partie réceptrice ne se projette pas sur une partie créatrice potentielle et vice-versa ? La phrase commençant ce paragraphe doit nous mettre en garde contre un possible oubli des divers acteurs participant à l'expérience musicale, mais aussi nous aider à cerner plus notre domaine. Nous explicitons, même si c'est redondant, que notre intérêt est focalisé sur l'aspect temporel de la composition musicale. L'activité du compositeur est située dans un univers musical (sons, silences, rapports harmoniques, etc.) et a pour intention de communiquer à un "autre" (auditeur, interprète, compositeur, ...). Dans le cadre de la CAO, nous sommes restreints à l'organisation des objets musicaux en laissant au compositeur la responsabilité de donner une sémantique à une telle organisation. Pour que le compositeur puisse construire le temps musical de l'autre, nous pouvons fournir des outils qui aident à la construction d'organisations "logiques" d'objets musicaux. Cet énoncé est évidemment fallacieux, en effet le terme "objet musical" peut déterminer une population hétérogène d'entités, de plus l'expression "organisation logique" semble mériter quelques lignes d'approfondissement.
La métaphore physiologique dans [Gris87] nous servira par la suite à dénommer différents niveaux du temps musical dans une composition. Dans ses réflexions sur le temps musical, G. Grisey aborde trois approches du temps musical qu'il appelle : le squelette du temps, la chair du temps et la peau du temps.
" Par squelette du temps, nous entendons le découpage temporel qu'opère le compositeur pour mettre en forme les sons ". A ce niveau, le compositeur est chargé de gérer le tempo, la métrique, ou n'importe quel autre paramètre qui intervient dans la construction d'un temps dans lequel la musique s'écoulera. L'unité de mesure de ce temps est quantitative, voir " chronométrique ", par exemple, la seconde. Cette approche du temps musical est la préférée de la plupart des compositeurs contemporains, de nos jours le vieux débat entre la musique comme forme d'expression ou comme architecture semble favoriser les moyens par rapport aux buts.
La chair du temps a à voir avec "...la perception immédiate du temps dans ses rapports avec le matériau sonore. " Dans cette approche, plus qualitative que la précédente, le compositeur s'intéresse à créer le temps musical comme " temps perceptible et non comme temps chronométrique " ou comme on l'a déjà dit, le temps est vu comme un élément de composition. La mesure de la chair du temps se fait en terme de " préaudibilité " qui peut être formulée comme le degré de prévisibilité du matériau sonore par rapport à une logique donnée. On sait que le degré de concordance ou de discordance entre des événements sonores a une influence dans la perception de la durée du temps chronométrique, bien que cette durée soit toujours constante. Ainsi, par exemple, l'introduction d'un événement qui perturbe une certaine "linéarité" du temps musical fixe un point de repère et réveille l'attention sur la suite du discours musical, dans ce cas nous dirons que le temps s'est contracté. Au contraire, un grand degré de prévisibilité dans une série d'événements aura pour conséquence une impression de dilatation du temps. Ces types de phénomènes sont à la base dans la composition des structures microphoniques. Nous l'avons déjà dit dans l'introduction de ce texte : l'union de l'espace rythmique et de l'espace sonore en tant que produit d'une logique commune est l'un des grands apports de l'informatique à la musique. Mais pour cela, le compositeur doit être capable de jouer avec le temps de façon à "donner du temps" à l'auditeur pour l'audition des structures microphoniques. Grisey formule, à ce sujet, une analogie avec le principe d'incertitude quantique, " l'acuité de la perception auditive est inversement proportionnelle à celle de la perception temporelle. "
" La peau du temps, lieu de communication entre le temps musical et le temps de l'auditeur, ne laisse que très peu de prise à son action. [du compositeur] " Si dans les deux premières approches, le compositeur doit faire face à son univers (univers musical), dans cette dernière il doit faire face à l'autre (auditeur, interprète, etc.). On est même tenté de dire qu'il doit jouer leur rôle. Pour cela, le compositeur laisse des traces afin que l'auditeur, en utilisant la plus indépendante des ressources de l'audition musicale : la mémoire, reconstitue le ou les temps musicaux contenus dans l'¤uvre. Dans le meilleur des cas, l'ambiguïté de ces traces mène l'auditeur à une démarche inverse en construisant un autre temps musical que celui voulu par le compositeur. Par rapport à la mémoire, Grisey parle de deux aspects : l'un qui favorise l'instant et la mémoire immédiate de l'événement sonore et l'autre qui s'appuie sur la mémoire cognitive de l'auditeur. Le premier peut être associé à une révélation des muses tandis que le deuxième sera de l'ordre de l'apprentissage. Dans le deuxième cas, qui nous intéresse le plus, Grisey parle de l'existence d'une entropie auditive qui force le compositeur à recourir en permanence aux artifices qui permettent à l'auditeur l'introduction d'ordre, car sans ordre il n'y a pas de temps musical. Malheureusement, dit-il, le compositeur ne dispose que de bien maigres moyens : la répétition (bien sûr), les accents (de tout type) et l'un des plus intéressants, le point de jonction entre le temps physique et le temps musical (le début et la fin d'une pièce sont des points stratégiques pour notre mémoire).
Une autre notion étroitement liée à la notion de temps est celle d'éternité. En ce qui nous concerne, l'éternité devient intéressante car elle est non seulement une forme d'absence ou de plénitude du temps, mais aussi en tant que relation à la question sur le début et la fin du temps. L'article de Stockhausen Wie die Zeit Vergeht, ([Stoc56], référence fondamentale selon nous) témoigne d'un mariage, encore d'actualité, entre rythme et timbre. Plus encore le " continuum " entre rythme et timbre, d'après Stockhausen, peut et doit être étendu à l'harmonie, la forme et en général aux divers composantes de l'¤uvre, pour créer ainsi une seule loi génératrice chargée de l'unité de l'¤uvre. La tentation est aussi grande qu'immédiate de concevoir les processus (sur n'importe quelle composante) comme des objets étirés dans le temps ou au contraire de concevoir les objets comme des processus compressés. Nous trouvons dans [Melc91] la citation suivante de Stockhausen : " La structure d'une ¤uvre ne se présente pas comme un déroulement ou un développement dans le temps, mais croît comme un champ temporel non directionnel... elle s'inscrit obligatoirement dans le moment présent, dans l'absence de temps, où les tempi et les rythmes ne jouent plus aucun rôle, sont profondément mis en péril... au début, au développement, ils sont finalement abolis... passé, présent et futur ne feront qu'un... les événements musicaux n'ont pas un cours fixe dans un parcours déterminé et une fin inexorable, les moments ne sont pas purement la conséquence de ceux qui les précède et antécédents de ceux qui les suivent ; plutôt la concentration sur l'Instant - sur chaque Instant comme s'il était une sorte d'indécision verbale coupant transversalement chaque conception horizontale du temps et qui mène à l'absence de temps, à ce que nous appelons l'éternité : une éternité qui ne commence pas à la fin du temps, mais qui peut être atteinte à l'intérieur de chaque moment. " A cette recherche d'une musique sans direction, éloignée du sentiment du temps musical, Melchiore s'oppose en expliquant que " Les modalités qui définissent ce refus du temps, qui idéologiquement aspirent à un présent éternel sans passé ni futur, techniquement peuvent se rattacher à une tendance dominante vers l'abstraction : abstraction d'une donnée sonore, d'un matériau et abstraction du processus sonore, de la forme. " La démarche de Stockhausen, fort intéressante sur le plan artistique, ne peut pas induire la négation d'une direction musicale. Dans la musique, on n'a pas trouvé d'atome insécable constituant toute composition. Le choix d'étendre les relations microphoniques aux objets sonores au niveau de la forme n'a pas de validité tant qu'on ne saura pas s'il existe une validité musicale des relations strictement acoustiques. Nous associons la construction d'un temps musical par un compositeur aux diverses relations qu'il crée entre le matériau, cependant nous ne pouvons pas supposer que les relations sont à la base de ce temps musical ; une erreur aussi grande serait de penser que ce sont les objets qui constituent l'étalon temporel d'une pièce ; et plus naïf encore serait d'énoncer, tout simplement, que le temps musical est fait de relations et d'objets (c'est-à-dire de matériau et d'organisation). Donc, nous concevons le temps musical comme le produit du point de rencontre d'un ensemble de relations entre objets, voir d'un ensemble de temps. Nous postulons aussi que le temps musical et sa direction sont indispensables dans la composition.
Après avoir posé l'axiome de l'existence de la direction du temps musical, nous nous concentrons sur les divers types de direction. En ce qui concerne le temps musical, est-il linéaire ou arborescent ? A-t-il des cycles ou est-il irréversible ? Y a-t-il une direction générale du temps musical ou chaque pièce a-t-elle une direction propre ? Dans [Live92], Pierre Livet définit le temps musical comme un temps ramifié, sans cycle et avec un retour à la linéarité. Le raisonnement qui soutient cette affirmation est que si nous écoutons une mélodie et un contrepoint, le temps bifurque car nous sommes incapables de suivre indépendamment chaque partie car ces deux modes musicaux sont analysés par des moyens de traitement cognitif différents. Cependant il nous est possible de traiter ces deux modes musicaux de manière fusionnée et ainsi il y a un retour à l'unité, voir à la linéarité. Pour sa part J. D. Kramer, dans [Kram88], proclame que l'¤uvre musicale est composée de linéarité et de non linéarité. La linéarité étant définie comme "...the determination of some characteristic(s) of music in accordance with implications that arise from earlier events of the piece. ". La non linéarité à son tour est "...the determination of some characteristic(s) of music in accordance with implications that arise from principles or tendencies governing an entire piece or section. ". Selon ces définitions, l'exemple typique de linéarité est la musique tonale. Une pièce tonale est gouvernée par un but : le retour à la tonique. Ce retour à la tonique est un acquis, contrairement au chemin que l'on suit pour y arriver.
Nous allons maintenant exposer notre point de vue qui diffère de la position des auteurs cités précédemment, mais nous devons d'abord nous prononcer sur le mouvement dans une composition et sur la notion de temps cyclique. Nous distinguons deux types de mouvements : l'un sans mobile, indivisible et qui se suffit à lui-même, par exemple une mélodie ; l'autre est un mouvement qui peut être divisible en parties fixes, par exemple l'apparition d'un thème lors de diverses occasions produit un mouvement dans lequel le mobile est le thème. Dans ce dernier cas, si l'objet qui se meut est considéré comme une unité ayant un temps similaire au premier type de mouvement, alors l'idée d'un temps cyclique devient envisageable. Nous avons défini le temps musical comme le point de rencontre de divers temps ou relations. Bien que nous approuvions la réversibilité et la non linéarité de la peau du temps (c'est-à-dire le temps que l'auditeur construit), nous restreignons les relations constituantes du temps musical à n'être que des ordres linéaires .Grâce aux divers points de rencontre de ces temps et aussi à l'emboîtement de ces relations temporelles, nous pouvons faire apparaître la réversibilité et la non linéarité souhaitées.
Pour parler de continuité dans la musique, nous nous basons sur l'article [BrLe98]. De manière générale et intuitive, les auteurs définissent la continuité de manière sensorielle : " Nous considérons pour notre propos qu'une chose est continue si nous n'en percevons pas la discontinuité. ". En ce qui concerne la musique, il est possible de distinguer deux pôles : la discontinuité extrême de l'aléatoire et la continuité maximale de l'immobile. Le compositeur a à faire avec ces deux extrêmes, par exemple le retour d'un événement après un passage aléatoire définit une "...mise en continuité entre deux instants de l'écoute. " Cette notion de continuité peut, sans trop de difficulté, être associée aux relations entre objets dont nous avons parlé. Sur le plan du temps physique nous nous retrouvons dans le cas d'un mouvement constitué de primitives. Mais ce qui constitue l'intérêt majeur de cet article est l'abstraction des phénomènes physiques mesurables, pour se placer dans un contexte " topologique ". De ce point de vue, la continuité joue un rôle fondamental. " On dit que deux objets sont topologiquement équivalents, s'ils peuvent être transformés l'un en l'autre par une transformation continue. " Cette notion de topologie peut s'appliquer aux objets comme aux processus. Si nous nous intéressons aux diverses possibilités de combiner les processus, nous rentrons dans la structuration de la pièce.
La fin de ce chapitre ne prétend en aucun cas donner une définition de temps musical. Nous avons analysé certains aspects du temps musical afin d'établire un compromis entre une possible formalisation théorique et la possibilité de construire des outils informatiques pour son exploitation.
Dans les divers travaux portant sur la modélisation du temps, nous distinguons deux groupes principaux d'approches : numérique et logique. Il est à noter que la plupart de modèles temporels implémentés en CAO appartiennent au premier groupe. La majorité d'entre eux ont comme principale caractéristique l'irréversibilité et la linéarité ; ils sont donc applicables à un niveau très proche du temps physique. Ceci ne veut pas dire qu'il n'existe pas de modèles adaptés à la musique (dans la plupart à la performance). Un représentant typique de ce groupe d'approche est QuickTime. QuickTime définit un système de coordonnées temporel fini, discret et absolu, rapporté à une réalité temporelle commune : la seconde. L'espace temporel, ainsi défini permet l'insertion d'événements temporels à un point donné. À son tour, chaque événement en QuickTime a son propre système de coordonnées, constitué d'une échelle et d'une durée. L'échelle est chargée de la transition entre le temps relatif à la donnée et le temps absolu. La durée est exprimée dans une unité définie par cette échelle. Des objets temporels complexes peuvent être construits dans ce modèle à l'aide de l'opération d'emboîtement. Ce type de modèles n'est pas très adaptés pour gérer la notion du temps qu'on a associé à l'expression "squelette du temps". En effet, les phénomènes d'accelerando et rallantendo ne peuvent pas être représentés avec un simple facteur de scaling. Dans [MaZa94], nous avons étudié la notion de courbe de tempo, qui nous a servi pour modeler les accellerandi et rallentendi dans notre projet de quantification rythmique [AgAs95]. L'idée de base consiste à remplacer l'échelle par une fonction dite courbe du tempo et de n'appliquer les effets de cette fonction qu'aux objets de premier niveau dans la hiérarchie d'emboîtement afin de ne pas casser les sous-structures rythmiques de bas niveau (par exemple, des triolets ou quintolets à l'intérieur d'une mesure). En général il s'agit de rattacher les espaces e (temps physique) et E (le squelette du temps). Pour cela, nous supposons qu'il existe une transformation :
![]() telle que
telle que ![]() est une fonction continûment
différentiable.
est une fonction continûment
différentiable.
La courbe de tempo T associée à une transformation
![]() est définie par :
est définie par :
![]()
Ainsi si on connaît un temps initial ![]() la transformation
la transformation ![]() peut
être exprimée par l'équation suivante :
peut
être exprimée par l'équation suivante :
![]()
Nous groupons sous l'approche numérique les structures de représentations temporelles définies dans 3.1. Les modèles temporels numériques ne s'avèrent pas les plus adaptés pour le traitement du temps musical tel qu'on l'a conçu dans cette section. Il est clair, que les outils informatiques en CAO ne peuvent pas s'en passer d'un modèle de représentation temporelle numérique, en particulier quand il s'agit de l'axe perception dans notre trilogie : langage, notation et perception.
L'approche logique semble être plus adapté pour la gestion d'un temps musicale qui impose plutôt une topologie qu'une forme. Nous pouvons remarquer dans les paragraphes précédents que nous ne nous sommes pas interrogé sur la nature du temps musical. Notre interet porte sur comme exprimer certaines relations constituant le temps, evidement ce temps dont nous parlons n'a pas un autre soutient réel que la perception.
Nous serons obligés dans les travaux à venir de définire un langage logique, ainsi qu'une ou plusieurs modèles de basé sur des entités temporelles primitives. Nous sommes intéressés par des modèles temporels qui nous permettent de traiter des figures comme la répétition, l'ambiguïté du choix pour le futur (branching) et en général l'organisation des objets dans le temps autre que le modèle conventionnel, avant et après.