Bernard Bel
CNRS -- Centre de Sciences Humaines
2, Aurangzeb road, New Delhi 110 011, India
bel@csh.delnet.ernet.in -- Fax (91) 11 301 8480

Abstract

Most computer music environments privilege music representations derived from western common music notation, which make it difficult to explore musical ideas based on different concepts. This is notably the case with Indian composers eager to handle sophisticated note treatment and complex polyrhythmic structures.

This paper presents recent developments of a compositional environment, Bol Processor BP2, addressing the issue of abstract and comprehensive, altogether flexible and accurate, music representations.

Keywords

Computer music, computational musicology, music representation and performance, sonology, sound objects, polymetric structures, Bol Processor BP2

Software for music composition often relies on music representations privileging the twelve-tone system and binary divisions of time intervals. Graphic display of western common music notation and the MIDI standard contribute to reinforce this conventional approach. Indeed, advanced MIDI sequencers allow the fine control of parameters such as microtonal pitch, channel pressure, etc. But these are generally part of 'expressive' or 'ornamentative' techniques, whereas the skeleton of musical pieces remains basically a twelve-tone pattern in metronomic tempo. In this context, musicians conversant with non-European musical systems have little or no access to the melodic subtleties and rhythmic intricacies of their musical heritage.

In India, a country both famous for musical diversity and achievements of its software industry, this lack of 'local' composition software is a great challenge to designers. Electronic instruments may quickly gain popularity in the rather conservative world of classical music, as they turn out to be more versatile for public performance than some traditional instruments whose sound gets distorted with bad amplification. Can an electronic keyboard with its pitch bender compete with a South Indian sarasvati vina (a plucked-stringed instrument) for which magnetic pick-ups only can capture melodic patterns in the bass register? The result may depend less on instrument design than on the skills and musicianship of its performer. Experience has already shown two points: (1) given a long time to train themselves, musicians can produce acceptable gamakas (complicated melodic patterns specific to Carnatic music) on electronic instruments; (2) the range of acceptability of tonal patterns tends to become broader when sound quality increases.

In the commercial scene ('film music' in India, 'global' music elsewhere), the situation is problematic as electronic devices lend themselves to mechanical performance. Whereas committed musicians may spend years practising pitch benders or electronic drums, a composer cannot 'implement' similar skills because of the lack of suitable representation models. Mixing vocal parts and a few typical acoustical instruments (the masala ingredient) on top of the electronic track seems to be the most successful recipe for modern music in a traditional context. As a result, present-day Indian music is becoming increasingly 'noisy', and with the fashion of taped music it is also contaminating contemporary dance and drama.

This paper addresses the question of a flexible environment for non-European music composition, in response to the concerns expressed in the discussion of Indian music. It introduces recent developments of a computer software, the Bol Processor, based on initial studies of improvisatory methods used by North Indian tabla drummers (Kippen & Bel 1992).

1. Bol Processor BP2 -- the task environment

Compared with well-known computer music environments like Max and Keema, BP2 has much less advanced real-time and interactive features, but it claims a more straightforward control of 'long-term' processes thanks to its inference engine. Besides, we feel that the development of music programs should concentrate on their ability to 'collaborate' by exchanging MIDI messages, Apple Events, etc., rather than on the integration of so-called 'complete' features. Desktop publication software has already proved the efficiency of this type of design.

There are three typical ways of producing music with BP2. A grammar may describe a set of musical pieces (a formal language) produced randomly and played in sequence -- for instance Mozart's musical dice. This is the 'Improvise' mode, in which MIDI input may also be used to monitor processes (e.g. synchronise the performance). A grammar may otherwise describe a unique musical piece. This is particularly useful for complex structures that require a comprehensible hierarchical description. The third method is to edit or import a musical score, ignoring the inference system.

2. Prescriptive and descriptive representations of music

The 'interpreter', whose role is to transform scores to streams of sound events, may be viewed as the sonological component of the representation.

A well-formed musical score should contain all relevant information in a concise and comprehensive format. The missing information is completed by the interpreter on the basis of rules deemed 'acceptable' for music performance. Human interpreters follow a large number of explicit (and implicit) rules capitalised in their training. Their musical notation, therefore, is to a large extent prescriptive rather than descriptive. In computer music, where the focus is put on explorative tasks -- in Laske's words (1993:211), possible musics rather than existing musics -- interpretation rules should be restricted to widely accepted conventions and completed with explicit information supplied by musicians (and their environment if the system is interactive).

A descriptive notation, in which all musical events are explicit, is neither convenient for humans nor computationally efficient. Most graphic design programs, for instance, contain tools for drawing straight lines, circles and polygons, which lend themselves to simple geometrical descriptions (vector, instead of pixel, representations). Beyond these conventional shapes, designers may either be offered an extended library (arcs, ellipses, parabolas...) or resort to pixel hand-drawing.

'Pixel' representation is the only solution today for an Indian musician wanting to produce delicate note connections (alankara or gamaka) using a conventional sequencer: every 'PitchBend' message needs to be defined and stored in memory or in a MIDI file. So far, 'shape tables' or predefined formulae do not exist, and may never be defined given the stylistic diversity.

In graphic design, new techniques have been developed, such as polygonal and Bézier curve fitting, to combine flexibility, accuracy and vector storage. This is the approach followed in BP2 for the representation of all dimensions of electronic sound, including time.

The question of well-accepted conventions is culture-sensitive and therefore arguable. Musical scales, tonality and harmony are in no way universal concepts. In order to gain acceptance, conventions must stand at a high abstract level that does not interfere with local musical concepts. For instance, when representing music as text, it is convenient to agree that symbols shall be written in chronological order -- the order of symbolic time. The mapping of symbolic to physical time remains a separate issue (Jaffe 1985, Bel 1992:69-70). Given rules for sequentiality, special operators are required to represent simultaneity (see polymetric structures).

3. The sonological level in BP2

3.1 Time-objects and sound-objects

Basic sequences of messages are called 'time-objects'. These are mapped to musical 'segments', thereby meaning either elementary musical gestures (e.g. strokes on a drum) or the resulting sounds. Time-objects are instances of prototypical sequences defined in sound-object prototypes. Once a time-object has been assigned sonic properties (metrical and topological) it may be termed a 'sound-object'.

A typical sound-object is a pair of 'NoteOn' and 'NoteOff' messages on the same key number and MIDI channel. This is a called a 'simple note' in BP2. Simple notes are labelled in English, French or Indian notation with an octave number, for instance 'A4', 'la3' and 'dha4' respectively for the conventional 440Hz tone.

3.2 More about sound-objects

Many bols like 'dha', 'dhin', etc., represent unique or simultaneous hand strokes. But there are also combined bols like 'tira' or 'kita' (two strokes) and 'tirakita' (four strokes). It would be tempting to segment them as 'ti', 'ra', 'ki', 'ta', but they are conceptualised as elementary segments; besides, their duration is a single time unit. The following vocalised examples will make it clear:

Let us suppose that the tempo is faster than 2 beats per second, and 'dha' has a minimum 0.5 second duration. The next sound-object ('tira' in the first example) will be partly overlapped by the resonance of 'dha'. This might not sound realistic. If so, it is convenient to truncate the end of 'dha'. Two topological properties need to be considered here: (1) how much of the end of 'dha' can be truncated? (2) how much of the beginning of 'tira' can be overlapped? Answers may be absolute time (e.g. don't cover more than 200 ms of 'tira') or percentages of sound-object durations.

A musical structure is often constructed on (possibly irregular) pulses. This is referred to by Boulez (1963:107) as striated time (temps lisse), opposed to smooth time (temps strié) in which no pulse is necessary (e.g. the alap of Indian music). We use the word 'time streaks' to designate pulses. Positioning a simple note on a time streak is straightforward: its 'NoteOn' message coincides with the streak. However, there is no such rule with sound-objects. The specific time point of the sound- object which should be anchored to the time streak is called a 'pivot' (Duthen & Stroppa 1990). A pivot may be placed anywhere irrespective of the time-span interval of the object. This interval is the one containing elementary actions (messages sent to the sound device), but the pivot relates to perceived sound, which may have its own time-span interval.

Some sound-objects do not contain a specific 'climax point' eligible for a pivot. By default, the beginning of their time-span interval is located on the time streak, but if necessary the sound-object may be shifted to the past or the future. Objects with time- pivots may also be shifted within specified limits (absolute or relative). An object that can be shifted unrestrictedly is called a relocatable sound- object.

3.3 Out-time sound-objects

3.4 Input objects

3.5 Smooth time and time-patterns

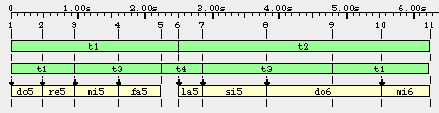
(in which '_' is a silence and '_' is the prolongation of do6) and constrained to a structure of time-patterns (a join-semilattice of time-span intervals). Time streaks are numbered 1 to 11.

==> sound example

(A discussion of this example may be found in Bel 1996:48)

3.6 Time-base

3.7 A sound example

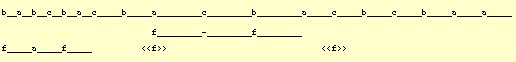
Metrical properties: the definition of sound-object prototype 'a' states a duration of 750 ms against a reference metronome period of 1000 ms. This means that the physical duration of 'a' will be 0.75 times the interval between two time streaks. Similarly, 'f' has a reference duration of 250 ms, but it cannot be contracted.

Topological properties: object 'a' is relocatable, and continuity must be 'forced' on its beginning. This means that relocatable sound-objects should be displaced until there is no silence preceding 'a'.

The resulting location of sound-objects on physical time is shown on the following graphic score:

==> sound example

4. Interpreting symbolic representations

4.1 The "period" notation of sequences

is interpreted as a sequence of nine beats in which each of the first three beats contains a single time-object, the following three beats contain two objects, and the remaining ones three objects. Subdivisions of beats are equal. In western notation with a 4/4 measure, we would say that the piece starts with crotchets and goes on with quavers and triplets. In North Indian music/dance these 'speeds' or 'bol densities' are called hargun (1), dogun (2) and tigun (3).

In previous versions of BP2 the (still valid) equivalent representation was:

Expression "/2" (an explicit tempo marker) indicates the beginning of 'speed 2' (dogun). The initial "/1" is the default speed and may therefore be omitted. This old syntax is less flexible than period notation because it forces 'absolute' tempo assignments. The possibility of 'resizing' symbolic durations is important when sequences are used as building blocks in a grammar, or fields of polymetric structures.

Period notation provides a simple process for BP2 to quantize correct durations in real time when sequences are played on a MIDI keyboard. The basic idea is that the program plays metronome ticks and prints a period after each tick. Notes played on the keyboard between two ticks are inserted between periods (thereby assuming that their durations within a beat are equal).

4.2 Prolongation symbols, non-integer durations

4.3 Curled brackets

Each sequence starts at 'speed 1' (default). The first beat of the first sequence contains one time-object. Beat duration, therefore, is one time unit. The second sequence also starts at speed 1, but its first beat contains two time-objects. Therefore beat duration in that sequence is two time units. This item is interpreted as:

The duration of the leftmost occurrences of 'a' and 'e' is 6/6 = 1 time unit, as expected.

4.4 Silences

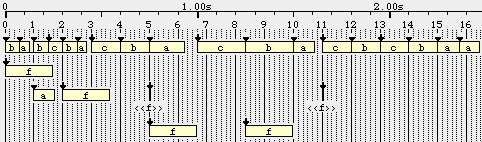
in which a silence lasting 4/3 time units is inserted in the sequence. Interpreting this item yields an expanded expression (an expression that contains no fractional duration),

or, equivalently, in period notation:

The graphic score of this item shows the disrupting of regular beats. After the silence, time streaks (numbered vertical lines) no longer coincide with '.' of the text score.

The internal representation used by BP2 may be called 'compact' in the sense that the interpreter minimises the number of prolongation symbols. This sometimes implies a 'rescaling' of the representation (Bel 1992: 81, dilation ratio). The advantage is that complex expressions require little memory space, thus complying with the 'vector' approach previously advocated.

4.6 Simultaneous events (polymetric structures)

The condition on equal durations is similar to the one in sequence operations. Therefore, the algorithm matching symbolic durations in polymetric expressions (Bel 1992:79) is the same one that operates on sequences. For example, the sequence

is interpreted:

Similarly, the polymetric expression

leads to the phase diagram:

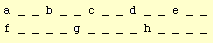
A convention is missing: what should be the symbolic duration of a polymetric expression? Clearly the duration of one of its fields, as suggested by single-field polymetric expressions:

If one of the fields contains an explicit tempo marker, then its duration -- hence the one of the entire structure -- is determined. (Since this may lead to conflicting durations, explicit tempo markers are not a recommendable design technique.) Otherwise, there are several ways of characterising the field used as a reference for duration: the longest or shortest (defined) one, and the leftmost or rightmost (defined) one. (Fields are 'defined' when they are not empty and they contain no undetermined rest.) The first option seems quite arbitrary; it had been proposed in Bel 1990 and was abandoned later. Besides, users often need to specify durations of polymetric expressions. The convention in BP2 is to set duration on the leftmost field. For instance, "{abc,de}" has a duration of three beats, against two beats for "{de,abc}".

Polymetric expressions are also useful to express complicated rhythmic divisions in sequences. This is done by putting a silence of the expected total duration in the first field. Thus, the expression

may be written:

Polymetric expressions accept multiple levels of bracketing. To this effect, the expansion algorithm is recursive (Bel 1990,1992:79).

4.7 Undetermined rests

A polyrhythmic piece "765432" composed by Andréine Bel for her Cronos dance production (1994) illustrates the use of undetermined rests. Six dancers were on stage: Suresh, Smriti, Olivier, etc. The parts they interpreted are indicated with variables bearing their names. The deep structure of the piece is:

This means, Suresh did his own part during the whole piece, whereas other dancers started 'some time later' and finished together. Undetermined rests were calculated on the basis of symbolic durations of each dancer's part, which was based on counting different cycles. For instance, Suresh had to count 14 times 7 beats, then 12 times 7 beats, then 10 x 7, and so on down to 2 x 7. Smriti counted 12 x 6, 10 x 6,..., 2 x 6. Olivier counted 10 x 5,..., 2 x 5. In the end, Andréine counted 4 x 2 and 2 x 2.

It is quite hard to calculate the resulting undetermined rests, leave alone representing them on a conventional score. BP2 takes care of it efficiently. A musician rightly identified this technique as "working on reversed time", a problem that is crucial in Indian rhythm.

5. Controlling performance

• Fixed: channel, transposition, MIDI switches (e.g. the 'hold' pedal);
• Stepwise: articulation, velocity;
• Continuous: pitch, modulation, channel pressure, volume, panoramic;

We introduce a few typical examples of stepwise and continuous controls highlighting the 'vectorisation' of BP2 representation. Although examples are based on simple notes in French notation, all these controls (except transposition) apply to sound-objects as well.

5.1 Stepwise control: example with articulation

The following example illustrates the interpolation of articulation controls throughout a polymetric structure. The piece starts with "_staccato(80)" (only 20% duration left) and ends up with "_legato(100)" (100% dilation, except for the last sound-object 'do4'). The second field of the polymetric structure "re5 mi5 do5 do5 la4 sol4" varies independently from "_legato(60)" down to "_staccato(40)".

The resulting graphic score (on the physical time axis) will be:

Changes are stepwise because parameter values vary only from one sound-object to the next. The handling of velocity is similar.

5.2 Continuous control: examples with microtonal pitch

• By default, 'x' is the numeric position of the current MIDI pitch bender (range 0 to 16383).
• If an instruction _pitchrange(r) has been found, 'x' is the value of the correction in cents, assuming that 'r' is the range of variation of the pitch bender on the current MIDI channel.

Thus, for instance, if the range of the pitch bender is +/- 2 semitones (+/- 200 cents) the second occurrence of 're4' in the following example will be performed 40 cents lower:

Pitch may vary stepwise, for instance in the following movement

which may be compared with a continuous variation:

Continuous pitch control on prolonged sound-object produces a portamento:

MIDI messages controlling continuous parameters are calculated in real time by the interpreter on the basis of specified intermediate values. Consequently, using complicated sound 'shapes' does not result in overloading memory or disk space. BP2 interpolation of sound parameters is similar to polygon line representation in graphic software. The default sampling rate for continuous control is 50 messages per second, but it can be readjusted for each parameter during the performance (instructions '_pitchrate()', etc.).

PitchBend values, and likewise all MIDI parameter values, may be captured from MIDI instruments. First, the editor is set to the "Type from MIDI" mode (which allows entering notes with the keyboard). Then the target "_pitchbend(x)" instruction is selected. Moving the pitch bender, then, automatically changes the value of its argument 'x'. If '_pitchrange()' has been found on the left, the value is displayed in cents.

Microtonal pitch may vary independently in several fields of a polymetric structure. Unfortunately, due to limitations of the MIDI system, these independent movements must be performed on separate MIDI channels. Therefore, channel assignments are required to tell the interpreter on which channels 'PitchBend' messages will be sent. For instance,

All performance parameters may be combined and interpolated independently. This makes it possible to control finely the evolution of sound, including its spatialisation thanks to panoramic controls. Below is an example of simultaneous pitchbend and channel pressure control on a single note 'do4':

These simple examples should not be viewed (and heard) as significant musical fragments. In spite of being vectorised, they remain low-level, rigid representations. The interesting musical part (beyond the scope of this paper) comes when sets of "well- shaped" patterns are produced by BP2's inference engine, using context-sensitive derivations or substitutions.

6. Conclusion

A majority of composers content themselves with predefined patterns or shapes. This is the case when working with 'standard' notation in a (dominant) musical idiom. Adventurous ones do not want to rely on design tools that would make restrictive assumptions on the material they are producing. Their work environment comprises both abstract representations and a proper mapping of these representations to concepts that they can manipulate in an intuitive (and creative) manner. BP2 claims to offer innovative solutions in that sort of environment. Doing so, it helps solving problems that require a great deal of human processing in other systems: accurate and flexible timing, incompletely defined polyrhythms, and vector representations of continuous parameter changes.

BP2 also makes it easy to design patterns in an abstract and systematic way (formal grammars, etc.), a feature that is not demonstrated in this paper (Bel 1992).

However, this may still be considered a preliminary phase... Current development focuses on two issues:

• Cooperation with other music software. This includes the sharing of MIDI ports (e.g. via Opcode Music System) and client-server technology. The latter is already operative thanks to Apple Events, but it will later be extended to other communication protocols like TCP/IP.
• Enhanced learning and pattern recognition techniques. Sequences of notes played on a MIDI keyboard can already be captured with proper note durations, but this recognition should gradually be extended to arbitrary streams of MIDI codes, including polyphonic patterns and the shape recognition of continuous parameter changes.

Although classical techniques (quantization of durations, Bézier curve fitting...) are envisaged to start with, their actual implementation is bound to require a great deal of investigation into what musicians consider significant. Quantization of durations, for instance, depends strongly on assumptions such as, notably, binary subdivisions of beats that western musicians take for granted although they do not hold in other musical contexts. Similarly, North and South Indian musicians are not likely to agree on the representation of a microtonal pitch pattern, which they perceive in different manners.

Even though it limitates itself to representation issues, this paper will hopefully project a clear idea of the approach followed for dealing with such problems.

References

Bel, Bernard

Symbolic and sonological representations of sound-object structures. In Understanding Music with AI, M. Balaban, K. Ebcioglu & O. Laske, Eds., AAAI Press, 1992:64-109.

Bol Processor BP2 reference manual, 1996. Distributed electronically with BP2 software: //ftp.ircam.fr/pub/music/programs/mac/BP2

Bel, Bernard, & Jim Kippen

Boulez, Pierre

Duthen, Jacques, & Marco Stroppa

Jaffe, David

Kippen, Jim, & Bernard Bel

Computers, Composition and the Challenge of "New Music" in Modern India. Leonardo, 4, 1994:79-84.

Laske, Otto