
Jacques DUDON, Atelier Exploration Harmonique, Les Camails, 83340 le Thoronet
Patrick SANCHEZ, LAS-CNRS, BP 8 13376 Marseille, sanchez@astrsp-mrs.fr
Résumé : La synthèse photosonique utilise des disques conçus et réalisés sur ordinateur. Nous présentons ici un nouveau logiciel d'aide à la conception de disques photosoniques : "WaveLoom" ainsi que d'autres outils de recherche et de création. Ce logiciel est basé sur la compilation d'un langage développé par l'Atelier d'Exploration Harmonique.

Figure 1 : Lecteur photosonique et séquenceur
Traits, secteurs et couronnes sont clairement visibles à l'oeil nu. Selon les disques, les traits peuvent varier de un à cinq millimètres de largeur et le nombre de couronnes de quelques unités à plus d'une centaine.
Les formes dessinées sur les disques ne sont pas forcément des couronnes mais peuvent être des déploiements de formes variées. L'instrument se joue à l'aide d'une source de lumière que l'on déplace manuellement. Ce faisceau intercepté par le disque vient se projeter sur une cellule photo-électrique en forme de croissant. Cette forme spécifique ainsi que le filtrage et la non-linéarité de la cellule donnent à cet instrument une couleur particulière.

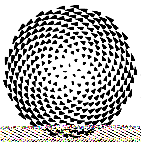

Figure 2 : quelques disques photosoniques
Parmi les degrés de liberté permis par ces disques, il y a l'interception du faisceau par un filtre en peigne. Celui-ci, suivant l'emplacement (manuel et variable) provoque une sélection de fréquences, en analogie avec les filtres en peigne numériques. En fait, la réponse impulsionnelle du filtre est inscrite sur une ligne verticale de cette image. Il est aussi possible d'intercepter la lumière, cette fois ambiante et non ponctuelle, par des disques séquenceurs (voir fig 1) tournant eux-mêmes à vitesse plus lente.

Figure 3 : un peigne d'interception
Néanmoins c'est la forme d'onde originelle inscrite sur le disque qui donne le champ exploratoire des timbres. Deux générations de logiciels ont permis de créer ces disques.
Ce procédé à servi à la création de quatre cent disques qui ont permis l'expérience de multiples paramètres reliant la géométrie des ondes et les sons, ainsi que l'élaboration de lecteurs arrivés aujourd'hui à un stade pleinement opérationnel. Une centaine de concerts ont été donnés sur ces instruments dont l'aboutissement est un premier compact disque (" Lumières audibles ") produit par l'Atelier d'Exploration Harmonique.
Ce logiciel, écrit en TURBO PASCAL 3.0 générait à partir d'un texte ASCII un ensemble d'instructions HPGL destinées au pilotage d'une table traçante. La précision du tracé des disques était entièrement dépendante de l'état de fonctionnement de la machine et des plumes. Un disque d'une complexité moyenne demandait un tracé d'une durée de huit heures environ. D'autre part le procédé ne permettait que le tracé d'à plats dont la largeur minimale était limité à l'épaisseur du trait de la plume (0.5 mm).
Le développement du logiciel à été réalisé à l'aide du langage VISUAL BASIC 4.0 sur un ordinateur compatible PC et s'intègre à WINDOWS 3.x ou WINDOWS 95. La visualisation des disques à l'écran a été rendue possible grâce à l'implémentation du logiciel " freeware " GHOSTVIEW. Cette visualisation permet un contrôle en permanence de l'état d'avancement de la création du disque.
Le langage de description des disques photosoniques est du niveau d'un langage machine : chaque phrase est constituée d'un code opératoire suivi d'un nombre variable de champ. Le code opératoire de base est celui destiné à la fabrication d'un " jour ". Un " jour " est l'espace laissé libre sur une couronne pour le passage de la lumière entre deux arcs opaques. Sur une couronne ces traits sont déterminés par deux angles (départ et arrivée) qui sont exprimés en inverse de tour. Le dernier champ indique la transparence du trait : cette valeur est comprise entre 0 et 1 (0 pour le noir, 1 pour le blanc). Par exemple pour tracer un arc de cercle entre 0 et 180deg. sur une couronne les données à indiquer sont :
J1 1 (0.0 0.5) 0.5
Une autre opération de base concerne le déploiement de l'arc défini en une couronne d' une largeur précisée par ses rayons minimal et maximal : DA 1 20 30
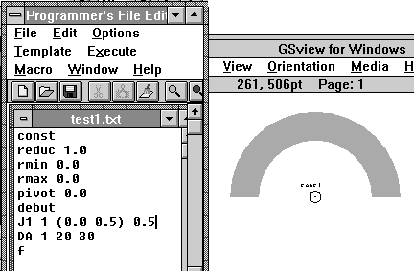
Figure 4 : Un exemple simple de création d'arc
Les codes opératoires représente un alphabet de 22 opérations de base telle que :
* Répétition d'onde
* Symétrie
* Pivotement
* Composition, omission
* Modulation de fréquence
* Effacement, élongation, compression etc..
* Addition, soustraction
Ces opérations permettent une grande richesse de création. De plus, la liste n'est pas exhaustive. Le langage s'est enrichit de fonctions permettant des transformations sur l'ensemble du disque (réduction, ajustement des rayons etc...) .
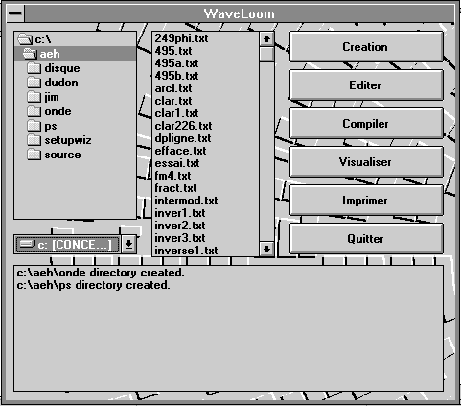
Figure 5 : un exemple de l'interface utilisateur
L'interface utilisateur est conçu pour simplifier les manipulations. Une opération de " glisser-déposer " permet l'édition, la compilation, la visualisation ou l'impression. L'éditeur est également un produit " freeware ", en l'occurrence il s'agit de " Programmer's File Editor" (PFE). Au cours de la compilation les erreurs s'affichent dans une fenêtre de contrôle.
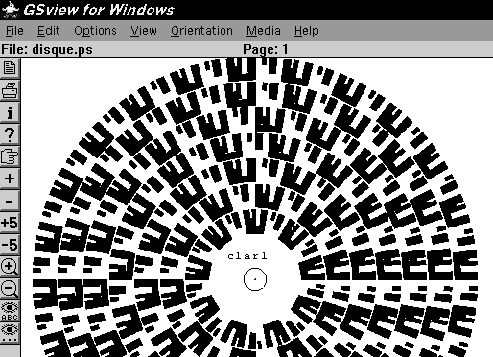
Figure 6 : onde fractale " clar ", échelle pentatonique
Cette nouvelle version comporte de nouvelles fonctions par rapport à la précédente mais est encore en expansion, par exemple une synthèse développée sur plusieurs couronnes à partir de sons réels ainsi que d'autres extractions à partir de sons naturels est prévue. L'intérêt principal de ce logiciel est d'intégrer dans une seule station de travail la conception et la réalisation de disques photosoniques avec une précision et une facilité de mise au point importante, notamment dans l'interactivité (visualisation immédiate des disques).
Il est intéressant de pouvoir connaître la relation entre les formes d'onde dessinées sur les disques et les spectres engendrés. Toutefois L'instrument de synthèse photosonique par lui-même ne fait pas que lire une couronne à la fois, mais il est cependant très utile de connaître à priori le résultat produit par chaque couronne. On trouvera donc dans les figures ci-dessous quelques ondes et leur transformée de Fourier réalisées avec le logiciel Matlab .
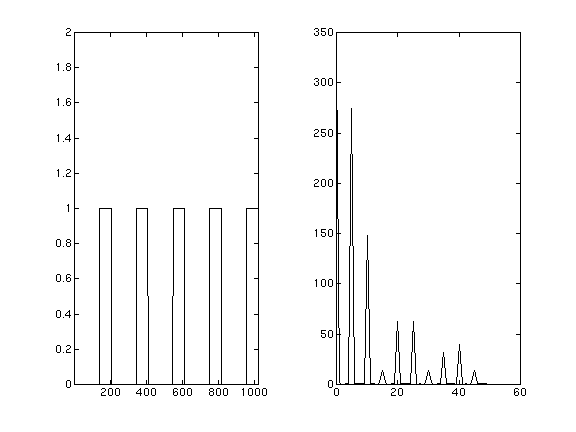
figure 7 : harmoniques réguliers
La première onde (en tout ou rien) est une succession de "trous" réguliers. Dans ce cas les fréquences sont les harmoniques multiples de cette fréquence de répétition. Mais la répartition de ces harmoniques dépend de la largeur du trou. Ainsi un "trou" de rapport cyclique 1/n verra les harmoniques k.n disparaître. dans cet exemple un cycle de répétition de 5, un rapport cyclique est de 0.32 provoquera un creux aux alentours des harmoniques 15,30,...
 o
o
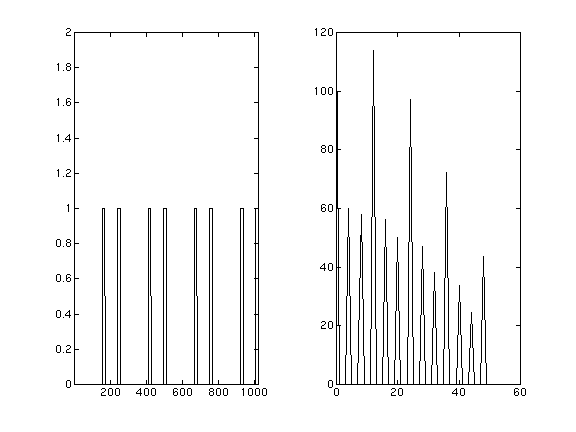
figure 8 : omission régulière
La deuxième onde est une "omission régulière". Cela veut dire qu'il y a deux cycles: celui des impulsions elle-même, qui est de 12 dans l'exemple ci-dessus, et celui de l'omission, qui est d'omettre un trou tous les trois, ce qui donne 4 omissions par tour. Dans ce cas, on constante que la fréquence de base est celle de l'omission, mais que l'harmonique prépondérant est celui des impulsons. L'effet sonore est donc celui d'une double note, l'une plus aigue et l'autre plus grave. La note grave peut en quelque sorte être considérée comme un sous-harmonique du son aigu En règle générale les disques utilisant ce procédé engendrent une gamme ascendante choisie sur des harmoniques élevés pour la fréquence des impulsions et pour l'autre séquence des divisions de ces fréquences qui forment une mélodie indépendante.
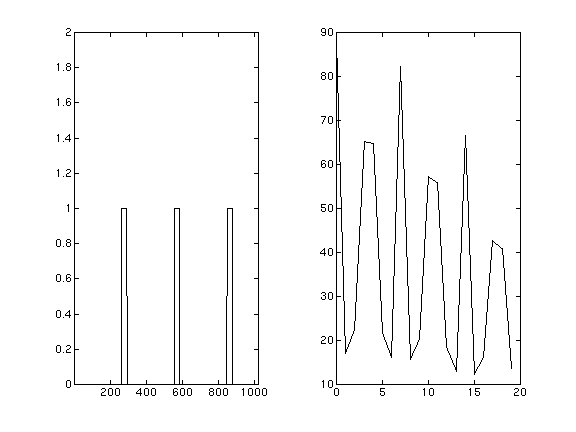
figure 9 : omission irrégulière
Quand l'omission est irrégulière, le phénomène est plus particulier puisque les harmoniques engendrés seraient multiples d'un nombre irrationnel. En fait cela est impossible, et il y accentuation des harmoniques autour de ces multiples, ce qui par exemple donne pour un rapport 3.5 une accentuation des harmoniques 3 et 4, puis 7, puis 10 et 11, etc..., mais l'effet perceptif est très ambigu.
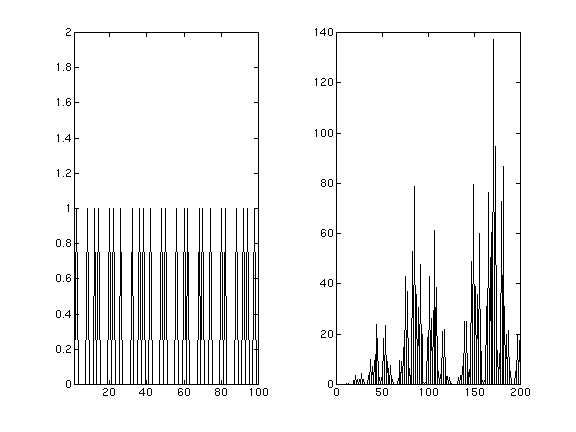
figure 10 : onde fractale
Les ondes peuvent être différentes de répétition classiques. En particulier on peut représenter des ondes fractales. L'exemple ci-dessus est engendré par la loi de récurrence suivante: Vn=(0 1)
Vn+1=(Vn 1-Vn)
autrement dit on concatène au vecteur son inversion, ce qui permet d'obtenir des ondes de longueur 4,8, 16, 32 etc.. Le spectre est très tourmenté mais avec uniquement des harmoniques impairs
[Dudon, 1996] Lumières audibles, CD, Atelier d'Exploration Harmonique,Les Camails 83340 le Thoronet