Patrick Fourcade (fourcade@imag.fr)
Claude Cadoz (Claude.Cadoz@imag.fr)
ACROE[1], 46 Avenue Félix Viallet
38000 Grenoble
Résumé. -- Cet article décrit une
étude et une simulation des processus de percussion à partir d'un
modèle élémentaire élaboré à l'aide
du formalisme CORDIS-ANIMA. Le modèle de percussion minimal est
basé sur une interaction à deux états entre deux masses
ponctuelles. Étudié selon toutes les possibilités de
variations offertes par ses paramètres, le modèle permet de
mettre en évidence des catégories sonores bien distinctes.
L'étude de ces catégories a été effectuée en
mettant en correspondance les trois formes de représentation : - le
modèle physique générateur, - le signal numérique,
- le phénomène sonore résultant et sa perception. Mots
clés : modélisation physique, synthèse sonore,
percussion.
Un des problèmes cruciaux posé par les techniques de
synthèse sonore est celui du contrôle. Si les formes perceptuelles
du timbre sont pour la plupart fidèlement reproduites, la gestion de
leur conduite, la maîtrise de leurs micro variations, en un mot
l'expressivité de la forme restent difficiles à réaliser
en terme de synthèse. Or une grande partie du travail de
l'instrumentiste est consacrée à cette notion : la palette
sonore. Celle-ci est liée lors de l'écoute au processus perceptif
de différenciation ; ce processus s'oppose au processus d'identification
de la source sonore rattaché à la forme du timbre [Castellengo
1987].
Nous faisons l'hypothèse qu'il existe des invariants perceptuels
(esthésiques[2]) basés sur la
relation physique : percuteur / objet sonore percuté. Ces invariants
seraient indépendants dans une certaine mesure du processus
d'identification de l'objet sonore présenté ; nous cherchons
alors un modèle générique de percussion pour les mettre en
évidence.
Nous utilisons le formalisme de modélisation et simulation des objets
physiques CORDIS-ANIMA (développé à l'ACROE, [Cadoz et al.
1990]).
Notre méthode d'investigation s'appuie sur une mise en correspondance
des trois niveaux de représentation en cause : la description physique
du modèle de production, la perception du son, l'analyse du signal.
Le phénomène de percussion résulte du choc physique entre
une structure vibrante et un percuteur ; l'interaction a par essence
un caractère fortement non-linéaire et concerne au moins deux
objets. La loi de Hertz stipule que le contact normal entre deux corps
hookéens est du type F=A.U1,5 ou F est la force
exercée, A une constante et U la compression des deux corps. [Doutaut et
al. 1994] ont modélisé la percussion d'une barre vibrante
avec ce type d'interaction. Par ailleurs, d'après les études
menées sur le piano par [Boutillon 1988], le contrôle par le
pianiste de la percussion d'une note isolée se réduit à la
communication d'une vitesse au marteau. Enfin, souvent la tête du
percuteur est recouverte par un matériau déformable comme le
feutre ou le caoutchouc. Le feutre des marteaux de piano joue un rôle
important lors du contact percuteur / structure vibrante. Il se déforme
élastiquement et absorbe une partie de l'énergie. Un
modèle simple est de considérer une interaction de type
F=AUp ou p est un réel [Ghosh 1932].
Expérimentalement, p est compris entre 2 et 3 d'après [Stulov
1995]. Deux modèles plus raffinés proposés par [Stulov
1995] et par [Boutillon 1988] prennent en compte le comportement
hystérétic du feutre. De ces études sur la percussion
pianistique et sur la percussion de lames vibrantes, nous retiendrons l'aspect
non-linéaire du processus d'excitation mais nous garderons la
linéarité des propriétés viscoélastiques du
corps intermédiaire.
Partant de ces considérations nous avons mis en oeuvre un modèle
de percussion élémentaire. Il nous semble intéressant
d'explorer le potentiel sonore d'une relation linéaire traduisant la
compression d'un élément ad'hoc entre le percuteur et l'objet
percuté. Le percuteur est une masse ponctuelle Mp dotée d'une
vitesse initiale vop. La structure vibrante est une masse ponctuelle Mc
reliée à un point fixe par une liaison visco-élastique
linéaire de raideur Kc et de viscosité Zc. Nous l'appelons
Cellule. Le son obtenu est issu de la variation de la position de la masse Mc
au cours du temps. Le corps intermédiaire est modélisé par
une liaison visco-élastique linéaire de raideur Kl et de
viscosité Zl effective lors du contact percuteur-Cellule. Bien que Tous
les mouvements sont unidimensionnels selon l'axe y. On remarquera que dans ce
modèle volontairement simplifié, la prise en compte du geste
instrumental se réduit à la donnée d'une vitesse
initiale.
L'interaction est telle que lorsque la position
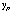 du percuteur est inférieure à la position
du percuteur est inférieure à la position
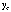 de la masse de la Cellule, la liaison viscoélastique de type
de la masse de la Cellule, la liaison viscoélastique de type
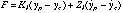 s'installe entre les deux masses. Dès que le percuteur est au-dessus de
la masse de la Cellule, la liaison disparaît. Le percuteur est alors une
masse libre. Nous appelons "butée viscoélastique" ce type de
liaison (cf Figure 1).
s'installe entre les deux masses. Dès que le percuteur est au-dessus de
la masse de la Cellule, la liaison disparaît. Le percuteur est alors une
masse libre. Nous appelons "butée viscoélastique" ce type de
liaison (cf Figure 1).
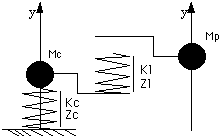
Figure 1. Modèle élémentaire de percussion. Mc, Kc,
Zc : masse, raideur et viscosité de la Cellule. Mp : masse du percuteur.
Kl, Zl : raideur et viscosité de la butée
viscoélastique.
ypo et yco étant les positions initiales respectives du percuteur et de
la masse de la Cellule, le système est décrit suivant l'approche
fonctionnelle ci-dessous :
(état libre) (état lié)
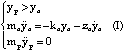
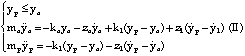
Les conditions initiales s'écrivent :
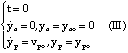
Ce système d'équations bien que trivial n'admet aucune solution
analytique.
La simulation en CORDIS-ANIMA du système (I, II, III) est
discrète. La discrètisation est telle que le pas temporel est de
Te. Les vitesses et les accélérations issues des signaux discrets
des positions respectives du percuteur (indice p) et de la masse de la cellule
(indice c) sont décrites de la façon suivante :
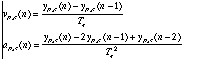
Le signal de force discret
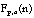 de la butée viscoélastique entre le percuteur et la masse de la
Cellule est tel que :
de la butée viscoélastique entre le percuteur et la masse de la
Cellule est tel que :
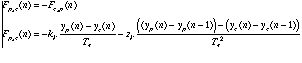
Nous explorons le modèle à partir des paramètres
physiques. L'espace des simulations de percussion est constitué de six
paramètres : la masse de la Cellule Mc, la raideur Kc et la
viscosité Zc de la Cellule, la masse du percuteur Mp, la raideur Kl et
la viscosité Zl de la butée viscoélastique.
Le paramètre Vpo, vitesse initiale du percuteur, n'est pas pris en
compte. Il a été fixé à 1m.s-1. En
effet, ce paramètre contrôle exactement l'amplitude du signal
sonore. Il suffit de remarquer que le système (I, II, III)
est invariant par une transformation de coordonnée
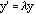 ou
ou
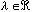 et que la modification de la vitesse initiale du percuteur revient à
faire ce type de transformation. On sait que la sensation d'intensité
sonore est relativement bien corrélée avec l'amplitude du signal
sonore. Elle varie à peu près suivant le logarithme de
l'amplitude. Dans un contexte sonore pauvre comme celui de la percussion simple
(son isolé) la relation se vérifie d'autant mieux.
et que la modification de la vitesse initiale du percuteur revient à
faire ce type de transformation. On sait que la sensation d'intensité
sonore est relativement bien corrélée avec l'amplitude du signal
sonore. Elle varie à peu près suivant le logarithme de
l'amplitude. Dans un contexte sonore pauvre comme celui de la percussion simple
(son isolé) la relation se vérifie d'autant mieux.
Chaque son simulé est l'objet d'une analyse en terme de signal.
En particulier, nous nous sommes intéressés aux grandeurs
suivantes :
- le temps de monté qui caractérise la durée entre
l'instant où la Cellule est au repos et l'instant où la Cellule
atteint une amplitude maximale ;
- le nombre de contacts lors de la percussion, défini par le
nombre d'aller-retour du percuteur vers la masse de la Cellule ;
- l'énergie transmise au système Cellule-butée par
le percuteur, égale à la différence entre l'énergie
cinétique du percuteur à l'instant initial et l'énergie
cinétique du percuteur après la percussion ;
- le rapport d'attaque, défini par le rapport entre l'amplitude
maximale de la Cellule lors de l'attaque et l'amplitude maximale de la Cellule
après le dernier contact.
Nous disposons des trajectoires temporelles du percuteur et de la masse de la
Cellule. L'analyse des sons par spectrogramme est réalisée
à l'aide du logiciel Audiosculpt développé
à l'Ircam[3].
Nous avons procédé à une analyse esthésique
des sons produits. Ils sont échantillonnés à 44,1KHz
et ont été calibrés préalablement. L'écoute
se déroule en deux étapes. Premièrement, les sons, dont
l'identification est masquée, sont groupés suivant leur
similarité perceptive. Deuxièmement, les groupes ainsi construits
sont réécoutés, réarrangés si
nécessaire, et font l'objet d'une description verbale. On
caractérise l'attaque et la résonance des sons de percussion
à l'intérieur de chaque groupe.
Nous avons fixé les paramètres de la Cellule pour une
fréquence de résonance de 503 Hz, un taux d'amortissement
de 2 s et une masse Mc de 10-5 Kg . Nous
appelons taux d'amortissement la grandeur [[tau]] homogène à un
temps telle que l'amortissement de la Cellule soit du type exp(-t/[[tau]]). On
en déduit Kc et Zc ; soit Kc = 100 N.m-1 et Zc =
10-5 Ns.m-1. Une exploration systématique
des trois paramètres restant Mp, Kl, Zl a été
réalisée. Les zones de divergences des simulations
numériques déterminent les frontières de l'espace d'
expérimentation. Le degré de résolution de ces
expérimentations est gouverné par la capacité à
discriminer deux sons voisins à l'écoute.
Ainsi, nous avons mené deux séries d'expérimentations. La
première est constituée de l'ensemble des combinaisons (Mp, Kl,
Zl) des grandeurs suivantes :
Mp = 10-7 , 10-6, 10-5, 10-4,
10-3Kg,
Kl = 1, 10 , 100 , 103, 104 Nm-1,
Zl = 10-5, 10-4, 10-3, 10-2,
10-1 Nsm-1 ;
soit 125 sons de deux secondes.
La deuxième est constituée de l'ensemble des combinaisons (Mp,Kl)
des grandeurs ci-après :
Mp = 10-7, 10-6, 10-5, 10-4,
10-3 , 3.16.10-7, 3.16.10-6,
3.16.10-5,
3.16.10-4, 3.16.10-3, 3.16.10-2,
3.16.10-1 Kg,
Kl = 1, 10, 100 , 103, 104 , 3.16,
3.16.101, 3.16.102, 3.16.103
Nm-1,
pour une valeur de frottement de liaison fixe, Zl = 10-5
Nsm-1 ; soit 90 sons.
L'étude des différentes formes d'attaque des signaux met en
évidence quatre configurations de courbe : d, dp, L et M. La figure 2
illustre les quatre configurations. Les évolutions au cours du temps des
positions du percuteur et de la masse de la Cellule sont
représentées ainsi que la variation de la force d'interaction
entre les deux masses.


Figure 2a Figure 2b


Figure 2c Figure 2d
Figure 2. Quatre configurations de signal : delta (d) : interaction
limitée à la communication d'une force, delta-p (dp) : similaire
avec rapport d'attaque>1, liée (L) : un seul contact, maillage
(M) : contacts multiples.
En analysant les différents timbres produits, nous avons
identifié six catégories sonores et deux qualités. Les
catégories sont désignées par les lettres A, A', B, B', C
et C', les qualités par les mentions attdbl et attsrd. La
qualité attdbl correspond à une sensation d'attaque
percussive double. La qualité attsrd est liée à
l'impression de hauteur subjective grave du transitoire. Il s'agit de
l'attribut de hauteur spectrale correspondant au centre de gravité
spectrale[4] (c.g.s.).
La catégorie A semble être représentée par un seul
candidat, un son de "sinusoïde amortie" sans identité d'attaque
perceptible.
La catégorie A' contient des sons A avec une attaque plus sèche ;
on remarque un léger effet de pincement.
Les attaques de la catégories B évoque un choc "massique" comme
la percussion de deux boules de billard. On a l'impression que les objets
percutés sont lourds.
Les timbres B', prochent de B, se caractérisent par le fait que la
sensation d'attaque double se situe au seuil de l'acuité temporelle. Un
référent posible est le bruit d'un sabot de cheval sur des
pavés.
Les attaques de la catégorie C s'apparentent aux consonnes labiales
comme le "B" ou le "P". Les sons C peuvent évoquer le bruit que fait un
bouchon de liège au sortir d'une bouteille ou encore celui d'un ballon
sous-gonflé percutant un sol en ciment.
La figure 3 montre la répartition des catégories à
l'intérieur de l'espace des paramètres physiques (Mp, Kl).
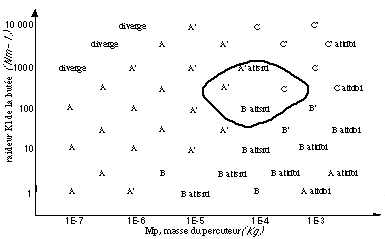
Figure 3. Correspondance poïetique-esthésique du percuteur à
Cellule fixe. A: son de "sinusoïde amortie", percussion neutre,
A': son A très sec, effet de pincement, B : son
"massique", choc de boules de billard, B' : son B au seuil de fusion de la
qualité attdbl, C : labiale, évoque la consonne "P", C' :
labiale, évoque la consonne "B", att dbl : qualité, sensation
d'une attaque double, attsrd : qualité, sensation de hauteur
spectrale grave
En mettant en correspondance ces deux analyses (figure 4) nous remarquons une
forte corrélation entre ces deux espaces de représentation. Il
est clair que l'attaque du signal contient potentiellement toute l'information
esthésique mais la sensibilité et la complexité
esthésique sont en général différentes de la
sensibilité et de la complexité dans l'espace du signal. Ici
elles sont comparables. Trois zones principales se dégagent avec un axe
tangible à masse du percuteur importante. Les paramètres de
production (paramètres poïétiques[5] ) varient beaucoup puisque l'échelle
est logarithmique. Le maillage réalisé décrit à peu
près la sensibilité auditive des opérateurs. En effet, des
explorations plus fines des paramètres Mp et Kl rendent difficile la
caractérisation esthésique. On remarquera un zone
particulière (encerclée dans la figure 3) qui contient les
catégories A, B et C.
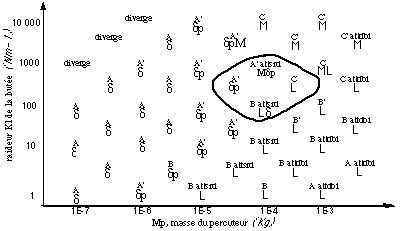
Figure 4. Correspondance poïetique-neutre-esthésique du
percuteur à Cellule fixe.
Les quatre configurations de signal combinées aux catégories
sonores nous ont conduit à parler de forme percussive.
forme d :
Elle est la plus représentée. Identifiable facilement, elle ne
comporte aucune nuance. Bien que l'espace des paramètres poïetiques
soit vaste, deux sons d ne pourront être
différentiés. Ceci se conçoit bien puisque l'interaction
percuteur-percuté se réduit à une force communiquée
durant environ 1/3 de la période de la Cellule. De plus, la Cellule se
comporte vis à vis du percuteur comme un un point fixe (masse
importante). Il y a identité entre l'information esthésique A et
l'information sur le signal, la forme d.
La forme dp :
Elle est très similaire à la
précédente. Deux contacts la caractérisent. La
différence au niveau du signal est dans le rapport d'attaque. Le
percuteur est renvoyé par la cellule qui perd alors une grande partie de
son énergie lors du deuxième contact. Ce phénomène
est analogue au renvoi du marteau par le front d'onde de la corde du piano.
L'amplitude de l'attaque est donc grande vis à vis de celle de la
résonance.
forme L :
Elle est caractérisée par une phase de contact relativement
longue. Elle illustre le comportement du système lié (II). La
masse du percuteur est grande. Les catégories B, B' et A sont
présentes. À masse du percuteur importante, quel que soit la
raideur de liaison, la perception d'une attaque double intervient. Il s'agit
nullement d'un rebond réel du percuteur sur la structure. L'effet
diminue lorsque Zc diminue. Durant la phase de contact, la Cellule qui oscille
a le temps de dissiper de l'énergie. Lorsque le percuteur refait
surface, il se comporte comme un générateur de force. La Cellule
est de nouveau excitée et s'amortit de nouveau. Un effet similaire est
obtenu lorsque Zl augmente (cf. 4.1.2 et figure 10 en annexe). Cette
qualité influence l'identification uniquement lorsqu'il y a
ambiguïté entre la perception d'une attaque simple ou double ;
c'est la catégorie B'. Les sons A observés à faible
raideur Kl et masse Mp importante traduisent le fait que les attaques de forme
L ne constituent plus une unité perceptive. L'excitation revient
à appliquer deux forces ponctuelles, l'une en début de contact,
l'autre en fin, entre deux instants grands par rapport à la
période de la structure vibrante.
Tab 1. Caractéristiques des formes percussives
génératives, les
grandeurs en italiques sont moyennées sur l'ensemble des sons.
forme d forme dp forme L forme M
masses Mp~ Mp~ Mc Mp~ Mp~
Mc/10 100.Mc 100.Mc
raideurs Kl~ Kl~ Kl~ Kc Kl~
4.Kc 16.Kc / 2 40.Kc
catégor- A A' B et C et C'
ies neutre pincemen B' "B" et
sonores t choc "P"
massiqu
e
Temps 0.7ms 1ms 15ms 5ms
de
montée
nombre 1 1.8 1 9
de
contacts
énergie 50% 8% 0.2% 1%
transmis
e
rapport 1 12 60 10
d'attaqu
e
forme
M :
Ici, la non-linéarité du processus intervient de façon
prépondérante. La raideur de liaison et la masse du percuteur
sont importantes. Les contacts sont multiples. Deux catégories sonores
correspondent à ce mode d'interaction. Les sons C' sont provoqués
par un nombre de contacts importants. Les sons C ont une
propriété remarquable : ils sont le siège d'une modulation
de fréquence durant l'attaque. Le sonagramme d'un son C avec une
fenêtre d'analyse très courte exprime clairement cet effet (cf.
annexe Figure 9.). Par filtrage, nous pouvons montrer que les hautes
fréquences sont responsables de cette identité.
Les formes génératives d, dp, L, M sont bien décrites par
la connaissance du temps de monté et du nombre de
contacts. Les combinaisons des critères nombre de contacts
et temps de montée permettent de regrouper les formes (cf figure
5)
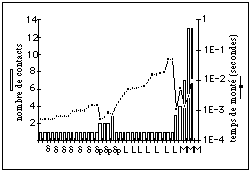
Figure 5. Variation du temps de monté et du nombre de contacts
par rapport aux formes percussives. Ces deux critères permettent de
grouper les formes percussives.
D'une manière générale, ce paramètre modifie
très peu la percussion tant sur le plan physique que sur le plan
esthésique. Lorsque Zl < 10-2 N.s.m-1, aucune
observation supplémentaire par rapport à la viscosité
nulle apparaît. Lorsque Zl > 10-2 N.s.m-1, pour
les percussions dont l'attaque est courte (<1ms) aucune observation
supplémentaire apparaît. En revanche, pour les percussions dont
l'attaque est longue (>10ms), typiquement la forme L et la forme M, la
sensation de l'attaque devient double sans altérer les
caractéristiques du timbre ; la figure 9 en annexe illustre cet effet
sur la forme L. Lorsque l'on filtre les énergies à basse
fréquence de ce son, on obtient deux sinusoïdes amorties
successives et la perception des deux attaques reste identique. Certes la
sensation de hauteur pour la première n'existe pas mais son
énergie, qui s'atténue au cours du temps, provoque la sensation
d'une attaque. Les oscillations à basses fréquences sont donc
responsables de ce phénomène. Dans le cas de percussion à
un contact, ce dédoublement correspond au choc et à l'anti-choc
du percuteur sur la Cellule. Il est une illustration de la symétrie
approchante du signal de force (cf figure 2b).
Au delà, pour un Zl plus important on observe que sur les trois formes
L, M, d, l'augmentation de ce paramètre provoque : - la diminution puis
la suppression des oscillations durant l'attaque, - la diminution du nombre
de contacts, - l'augmentation de l'énergie transmise, - la
diminution légère du Temps de monté.
Enfin, un phénomène très original apparaît à
percuteur léger (Mc/10) et à raideur de liaison très
faible (Kc/100). Il s'agit d'un changement de fréquence à
l'attaque. Le percuteur reste très longtemps au dessous de la masse de
la Cellule et vibre de concert avec elle (pendant 50 millisecondes). Cette
faible masse attachée à la Cellule diminue la fréquence de
résonance de l'oscillateur. Bien que faible physiquement, la masse
additionnelle représente 1/10 de la masse de la Cellule. Cela correspond
à un intervalle de hauteur de 70 cents ; cet intervalle se
perçoit tout de suite. Le timbre évoque une goutte d'eau (cf
figure 6).

Figure 6. forte viscosité ,faible raideur de la Butée
viscoélastique et percuteur léger : le percuteur vibre de concert
avec la Cellule durant 50 ms
Lorsque Zl est de l'ordre de 0.1 N.s.m-1, on atteint
rapidement une zone de divergence numérique.
Afin d'évaluer globalement l'effet de la structure sonore sur
notre analyse, nous avons été conduits à
expérimenter les variations des paramètres de la Cellule pour un
percuteur donné. Soit Mp = 10-5 Kg, Kl = 100
Nm-1, Zl = 10-5 Nsm-1 et Vop = -1
ms-1.
Nous avons expérimenté l'ensemble des combinaisons (Mc, Kc, Zc)
des grandeurs suivantes :
Mc = 10-7, 10-6, 10-5, 10-4,
10-3 Kg,
Kc = 1, 10, 100 , 103, 104 Nm-1,
Zc = 10-5, 10-4, 10-3, 10-2,
10-1 Nsm-1 ;
soit 125 sons de deux secondes.
La caractérisation esthésique est assez difficile. L'objectif
initial était de montrer la faiblesse de la méthode
d'expérimentation basée sur une Cellule vibrant à 503Hz.
Cette expérience n'a pas permis de dégager des relations
intéressantes.
Cependant, la variation de l'amortissement de la Cellule Zc provoque du point
de vue perceptif trois phénomènes très connus que nous
rappelons. À amortissement moyen, la modification du paramètre
est liée exactement à la perception de la durée de la
résonance du son. Elle ne modifie aucunement la perception de l'attaque.
À fort amortissement, la résonance disparaît. La perception
de l'attaque devient très différente. Il est possible que notre
système auditif se focalise alors sur la hauteur spectrale[6] de l'impact. À faible amortissement,
nous avons remarqué que l'identité de l'attaque se perdait au
profit de la résonance. Les détails qui peuvent nous guider dans
la ségrégation des attaques se noient si l'amortissement de la
Cellule diminue. Ceci est une évidence pour un analyseur
temps-fréquence. Plus le signal de percussion présente un faible
amortissement, plus sa réponse en fréquence est étroite ;
donc l'aspect temporel de ce signal est occulté par la dualité
temps-fréquence.
De plus, il est apparu, à l'issue du balayage en fréquence de la
Cellule percutée, des identités sonores ponctuelles et
très remarquables. Une forme d évoque fortement la percussion
d'un Djembé. Des percussions d'objets en verre sont apparues
également.
Si l'on décide de maintenir la Cellule à une fréquence et
à un taux d'amortissement constants, d'après les équations
I, II, III , un seul des trois paramètres Mc, Kc, Zc est libre. Nous
choisissons de faire varier Mc. En négligeant l'influence de Zl, le
système est constitué ainsi de trois variables
indépendantes : Mp, Kl, Mc (la vitesse initiale du percuteur ne jouant
aucun rôle).
Nous avons étudié l'ensemble des combinaisons (Mp,Mc,Kl) des
valeurs suivantes :
Mp = 10-7 ; 10-6 ; 10-5 ;10-4 ;
10-3 Kg,
Mp/Mc = 0,01 ; 0,1 ; 1 ; 10 ; 100,
Kl = 1 ; 10 ; 100 ; 1000 ; 10000 Nm-1,
Zl = 10-5 Nsm-1 ;
soit 125 sons pour fc=503Hz et [[Tau]] = 2 secondes.
L'analyse de ces sons donnent les mêmes catégories
esthésiques et les même configurations de signal que l'analyse
à percuteur variable. On retrouve les formes M et L pour un rapport
Mp/Mc grand, et la forme d pour un rapport faible. La différence est que
le lien entre les formes percussives et l'espace poïetique est
réalisé plus facilement. En effet, si on se place à
rapport Mp/Mc constant et Kl fixe, la variation simultanée des masses Mp
et Mc génère l'ensemble des configurations de signal. Plus
précisément, l'augmentation des deux masses, à fc,
[[tau]], Mp/Mc et Kl fixent, permet de passer de M à d, de d à
dp, de dp à L et cela suivant un ordre toujours respecté.
Lorsque le rapport Mp/Mc devient grand (de l'ordre de 100), les formes
percussives d, dp ne figurent plus ; le système passe continûment
de M à L (cf figure 7 et 8). Ce passage est important : d'une part car
la plus grande variété des identités sonores est
située dans cette zone (percuteur lourd ) ; d'autre part car la
variation des masses contrôle finement le nombre de contacts
réalisés. Ceci constitue le résultat essentiel de notre
étude.


Figure 7. Continuité poïetique d'une forme
liée Figure 8. forme LM , Kl = 100 N.m-1,
vers une forme maillage Mp = 10-3 Kg, Mc =
10-5 Kg.
Proposant un modèle de percussion élémentaire pour la
synthèse, nous avons exploré les potentiels sonores de ce dernier
en essayant de comprendre les trois niveaux de connaissances en cause. Nous
avons mis en évidence quatre formes percussives (d, dp, L, M) qui sont
liées pertinemment à la perception des sons simulés. La
première décrit une situation physique dans laquelle on peut
négliger le caractère non-orienté de l'interaction
percussive. La deuxième proche de l'excitation ponctuelle traduit le
phénomène du renvoi du percuteur par la Cellule. La
troisième est une percussion à un contact où les
propriétés du système lié interviennent de
façon prépondérante. La quatrième
génère des contacts multiples et fait intervenir le
caractère non-linéaire de la liaison. Les différents
paramètres du modèle pour générer des variations de
timbre audibles doivent varier suivant une échelle exponentielle. Nous
remarquons que plus la durée de l'interaction est longue entre le
percuteur et la Cellule, plus grande est la variété des timbres
obtenus. Nous avons vu que :
- la vitesse initiale du percuteur contrôle explicitement
l'intensité sonore ;
- la viscosité de liaison agit peu sur le timbre ;
- les masses et la raideur de la liaison contrôlent le timbre ;
- le temps de montée et le nombre de contacts sont
pertinents pour l'analyse esthésique.
Enfin la variation conjuguée des masses Mp et Mc, à rapport Mp/Mc
constant, pour une Cellule de résonance 503Hz et d'amortissement 2 sec.,
permet de passer d'une forme à une autre de manière continue et
d'ajuster finement le nombre de contacts.
Cette étude préliminaire sur la percussion permet de mieux
comprendre la non-linéarité de l'interaction
percuteur-percuté qui est commune à tous les
phénomènes de percussion. Un prolongement de ce travail consiste
à enrichir la structure vibrante et à faire le lien avec la
connaissance du modèle de percussion présenté. La
connaissance approfondie de la relation percussive permettra d'entrevoir les
palettes sonores des instruments de percussion. L'identité et
l'expressivité des formes de percussion seront ainsi accessibles. Des
structures virtuelles pourront être alors percutées avec toute la
richesse expressive d'une vraie relation musicale instrumentiste / corps
sonore.
[Boutillon 1988] Boutillon X., "Model for piano hammers: Experimental
determination and digital simulation",Journal of the Acoustical Society of
America, 83, 746-754.
[Cadoz et al. 1990] Cadoz C., Luciani A. et Florens JL. , CORDIS-ANIMA :
Système de modélisation et de simulation d'instruments et
d'objets physiques pour la création musicale et l'image animée,
Collection "Recherche Musique et Danse", Actes du colloque "Modèle
physique, création musicale et ordinateur" organisé par l'ACROE
Grenoble 90, Ed. Maison des Sciences de l'Homme, Paris 94.
[Castellengo 1987] Castellengo M., Les sources acoustiques, in D. Mercier (Ed.)
Le livre des techniques du son, tome 1, Paris, Editions
Fréquences, pp.45-70.
[Doutaut et al. 1994] Doutaut V. and Chaigne A., "Numerical simulations
of bar percussion instruments", Journal de physique IV, Colloque C5,
Suppl. JP III, Vol 4.
[Fourcade et al. 1996] Fourcade P. et Cadoz C., "Sound synthesis by physical
modelling: an elementary striker.", actes du colloque Forum Acusticum,
Antwerpen, Avril 96, suppl. 1.
[Ghosh 1932] Ghosh M. , India J. Phys. 7, pp. 365-382.
[Stulov 1995] Stulov A., "Hysteretic model of the grand piano hammer felt",
Journal of the Acoustical Society of America, 97, pp. 2577-2585.

Figure 9 percussion de forme L, sensation d'une attaque double.
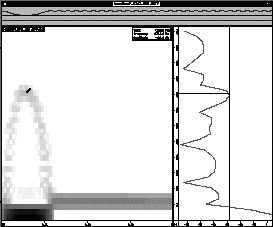
Figure 10 abscisse : échelle des temps en secondes,
ordonnée : échelle des fréquences en Hz, Les sons M sont
le siège d'une modulation de fréquence durant l'attaque.
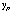 du percuteur est inférieure à la position
du percuteur est inférieure à la position
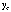 de la masse de la Cellule, la liaison viscoélastique de type
de la masse de la Cellule, la liaison viscoélastique de type
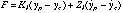 s'installe entre les deux masses. Dès que le percuteur est au-dessus de
la masse de la Cellule, la liaison disparaît. Le percuteur est alors une
masse libre. Nous appelons "butée viscoélastique" ce type de
liaison (cf Figure 1).
s'installe entre les deux masses. Dès que le percuteur est au-dessus de
la masse de la Cellule, la liaison disparaît. Le percuteur est alors une
masse libre. Nous appelons "butée viscoélastique" ce type de
liaison (cf Figure 1).
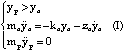
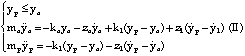
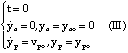
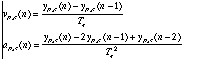
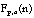 de la butée viscoélastique entre le percuteur et la masse de la
Cellule est tel que :
de la butée viscoélastique entre le percuteur et la masse de la
Cellule est tel que :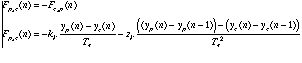
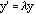 ou
ou
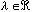 et que la modification de la vitesse initiale du percuteur revient à
faire ce type de transformation. On sait que la sensation d'intensité
sonore est relativement bien corrélée avec l'amplitude du signal
sonore. Elle varie à peu près suivant le logarithme de
l'amplitude. Dans un contexte sonore pauvre comme celui de la percussion simple
(son isolé) la relation se vérifie d'autant mieux.
et que la modification de la vitesse initiale du percuteur revient à
faire ce type de transformation. On sait que la sensation d'intensité
sonore est relativement bien corrélée avec l'amplitude du signal
sonore. Elle varie à peu près suivant le logarithme de
l'amplitude. Dans un contexte sonore pauvre comme celui de la percussion simple
(son isolé) la relation se vérifie d'autant mieux. 










