Todor Todoroff, FPMs, 9 rue de Houdain 7000 Mons, todor@musique.fpms.ac.be

Résumé: nous proposons un instrument de transformation par analyse-synthèse fonctionnant en temps réel dans l'environnement MAX-FTS. Composé d'un ensemble de nouveaux modules MAX externes, il autorise le contrôle de la plupart des paramètres à l'aide d'interfaces gestuelles MIDI (Clavier, boîtier de potentiomètres et de boutons, data glove, senseurs, ...) et permet donc la création de morphologies sonores ainsi que la transformation de sons instrumentaux en concert.

1. Introduction

Nous pensions qu'il était intéressant d'offrir les outils puissants de transformation par analyse-synthèse dans un environnement temps réel de manière à permettre une exploration plus rapide de l'espace des possibilités sonores, mais aussi pour permettre un contrôle gestuel précis des évolutions morphologiques. Plutôt que d'utiliser des modules MAX standard [Settel & Lippe, 1994], nous avons préféré écrire des modules externes optimisés afin de réduire le temps de réaction (transfert instantané des signaux par buffers mémoire et non par envoi de vecteurs de 64 échantillons par cycle) et d'offrir un contrôle plus étendu à l'utilisateur sans sacrifier la nécessaire modularité.

Parallèlement aux instruments de traitement de signal, nous développons de nouveaux modules graphiques de commande qui, programmés dans NeXTStep, permettent de communiquer avec FTS dans une architecture Client/Serveur. Ces outils nécessitent la nouvelle version de Max/FTS, actuellement encore au stade Bêta. Ils offrent des fenêtres de visualisation 2-D et 3-D ainsi que des moyens faciles pour assigner les données en provenance des interfaces gestuelles aux paramètres des traitements tournant sur FTS. Un compositeur pourra ainsi réassigner ses contrôles dans une interface visuelle simplifiée (ni modules, ni connections sans intérêt pour l'utilisateur qui encombrent les fenêtres MAX-FTS) sans devoir créer des modules, établir ou interrompre des connections. La philosophie générale de développement de ces interfaces graphiques et leur influence sur la création de morphologies sonores cohérentes est exposée dans [Todoroff, 1995].

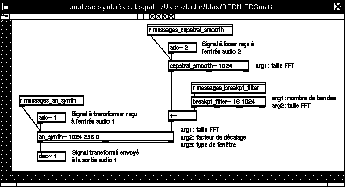
La chaîne de transformation est décomposée, pour plus de flexibilité, en plusieurs modules. On voit à la figure 1 le module de base an_synth~ qui reçoit le son à transformer et fournit à sa sortie le résultat de la transformation. Une fonction de transfert peut être générée par une combinaison d'autres modules: elle est obtenue ici en superposant un gabarit de filtrage fourni par le module breakpt_filter~ et le spectre lissé d'un signal auxiliaire en provenance de cepstral_smooth~. Toute les combinaisons de plusieurs modules fournissant des fonctions de transfert sont ainsi faciles à expérimenter. Nous décrirons en détail les différents modules actuellement disponibles en mentionnant les développements planifiés.

2. Module de base: an_synth~

Maillon principal de la chaîne de transformation, il analyse et transforme le son dans le domaine fréquentiel avant de le synthétiser. La transformation de signaux stéréophoniques nécessite l'utilisation de deux modules semblables en parallèle. Selon les paramètres d'analyse (taille de la fenêtre d'analyse et taux de recouvrement entre fenêtres adjacentes) il faudra alors utiliser un ou deux processeurs. Toutes les étapes de calcul, notamment la gestion des buffers et l'utilisation des fonctions de calcul de la FFT ont été optimisées afin d'autoriser sur un seul processeur l'analyse et la resynthèse par FFT à 1024 points avec un taux de recouvrement de 75%, ce qui équivaut au calcul simultané de 4 FFT directes et de 4 FFT inverses.

La séquence des opérations réalisées par an_synth~ est décrite schématiquement à la figure 2. On y a représenté le spectre d'amplitude pour plus de clarté, mais toutes les transformations se font simultanément sur les parties réelle et imaginaire.

Figure 1 : La chaîne de transformation.

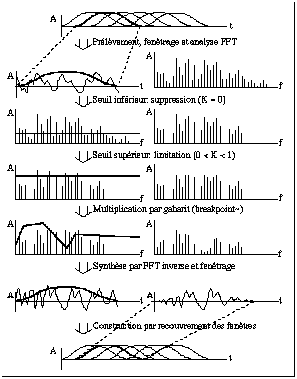
Figure 2 : Exemple de transformation effectuée par an_synth~.

2.1. Fenêtrage avec facteur de recouvrement de 50% ou 75%

Prélèvement d'une portion de 256, 512 ou 1024 échantillons du signal sonore d'entrée et multiplication par une fenêtre. La longueur de la fenêtre d'analyse ainsi que le facteur de recouvrement sont déterminés lors de la création du module. Le type de fenêtre utilisé (Hamming, Hanning, triangulaire, rectangulaire, cosinusoïdale) peut être modifié en temps réel par envoi du message adéquat à l'entrée du module.

2.2. Analyse par FFT à 256, 512 ou 1024 points

Nous tenons compte du fait que les signaux sonores sont réels pour optimiser le temps de calcul (relations de Bayard-Bode). Nous calculons les FFT de deux signaux réels en une seule opération de FFT complexe et nous récupérons ensuite, par addition et soustraction des parties paires et impaires, les parties réelles et imaginaires des transformées respectives de ces deux signaux. Cette méthode introduit un retard supplémentaire (il faut attendre d'avoir reçu les données de la seconde FFT avant de pouvoir calculer l'ensemble), mais elle permet par contre d'augmenter considérablement la qualité sonore en autorisant des facteurs de recouvrement supérieurs entre fenêtres d'analyse successives. Sans cette astuce, le taux de recouvrement maximal pour des analyses par FFT à 1024 points serait limité à 50%. Or, à 50%, on entend un effet de modulation induit par l'utilisation des fenêtres. Avec un recouvrement de 75%, c'est à dire avec un décalage de 25% entre fenêtres successives, cet effet secondaire indésirable disparaît complètement.

2.3. Traitement des données fréquentielles

2.3.1. Seuil inférieur

On teste dans chaque bande d'analyse si le carré de l'amplitude (on évite ainsi le calcul de la racine carrée pour des raisons d'optimisation) est inférieur au seuil. Si le test est positif, on multiplie les parties réelles et imaginaires par un facteur K. On peut donc supprimer la composante tombant sous le seuil (en la multipliant par zéro), l'atténuer ou encore l'amplifier.

On obtient ainsi soit un débruitage du signal, soit un effet qui pourrait être décrit en termes perceptif comme une espèce de "liquéfaction du son", soit encore une amplification des composantes de faible amplitude.

Les valeurs du seuil inférieur et du facteur K peuvent être modifiées en temps réel par l'utilisateur. Un seuil dépendant de la fréquence peut également être introduit graphiquement à l'aide de tables. Ceci permet, par exemple, de tenir compte des paramètres psychoacoustiques tels que seuil d'audition et sensibilité auditive afin de réaliser un débruitage à la fois plus efficace et plus discret.

2.3.2. Seuil supérieur

De façon similaire à l'application du seuil inférieur, le seuil supérieur permet de supprimer, d'atténuer ou d'accentuer les composantes fréquentielles dépassant le seuil. Ceci permet de modifier sélectivement de composantes sonores particulières, par exemple, d'atténuer des sons percussifs sans modifier les autres sons présents.

Remarquons que ces fonctions de seuil réalisent un filtrage adaptatif dans chaque bande de fréquence et permettent donc de réaliser des transformations sonores impossibles à obtenir dans le domaine temporel.

2.3.3. Multiplication par une fonction de transfert externe

Ceci revient à réaliser un filtre, une synthèse croisée ou les deux simultanément selon que le signal reçu soit un gabarit de filtrage (généré par exemple par le module breakpt_filter~ ), un spectre lissé provenant de l'analyse d'un autre signal (en provenance du module cepstral_smooth~) ou encore le produit ou la somme de plusieurs signaux. Les caractéristiques de filtrage sont bien sûr dépendantes du type de fenêtre utilisé.

2.3.4. Transpositions et décalages fréquentiels

Étant donné les limites de puissance de la carte, il n'est pas possible de faire le calcul de l'arctangente et de la racine carrée indispensable à l'extraction de la fréquence, de l'amplitude et de la phase avant transposition. Une optimisation plus poussée des différentes étapes du calcul et l'utilisation de tables permettra peut-être de résoudre ce problème. Nous proposons actuellement un zoom ou un décalage des parties imaginaires et réelles du spectre. Et, bien que le son obtenu ne soit pas très naturel, il y a là un certain nombre de transformations sonores qui, utilisées à bon escient, ont un intérêt musical. Les facteurs de transposition et de décalage fréquentiel peuvent être modifiées en temps réel par l'utilisateur.

2.4. Synthèse d'une portion de signal transformé

Nous veillons à ce que la représentation fréquentielle des signaux transformés ait une partie réelle paire et une partie imaginaire impaire. Nous pouvons alors calculer deux FFT inverses en une seule opération en utilisant les relations de Bayard-Bode. Il nous suffit pour cela de préparer les données fréquentielles de ces deux signaux de manière à ce que l'on retrouve, après calcul de la FFT inverse, le résultat de la synthèse du premier dans la partie réelle et le résultat de la synthèse du second dans la partie imaginaire.

2.5. Multiplication par une fenêtre

Les signaux audio synthétisés dans l'étape précédente doivent de nouveau être multipliés par une fenêtre car une modification du contenu spectral, notamment aux basses fréquences, détruit l'enveloppe du signal. Sans cette opération on introduirait des discontinuités dans le signal lors de l'étape suivante et celles-ci génèrent des "clicks" audibles.

2.6. Recomposition d'un signal audio continu

Ceci se fait par simple addition avec recouvrement des fenêtres de synthèse successives, en conservant le facteur de décalage adopté pour l'analyse.

2.7. Développements futurs

Les différentes expériences que nous avons menées lors du développement de ce module ont fait naître une série d'idées inédites que nous sommes en train de mettre en oeuvre. Certaines d'entre elles ne laissent planer aucun doute sur leur utilité. D'autres restent encore relativement abstraites et nécessitent des essais approfondis afin de les valider ou de les infirmer. Nous devons également vérifier s'il est possible de les réaliser dans les limites de la puissance de calcul disponible.

2.7.1. Prise en compte de l'évolution temporelle dans l'application des seuils: introduction d'une hystérèse et de filtres

Actuellement, les décisions sont prises indépendamment pour chaque fenêtre d'analyse. Nous étendrons les transformations fréquentielles en tenant compte de l'évolution temporelle (entre fenêtres d'analyse consécutives) de chacune des composantes fréquentielles.

L'introduction d'une hystérèse, en spécifiant un seuil de transition différent selon que la composante avait une valeur inférieure ou supérieure au seuil dans la fenêtre précédente, permettra d'éviter les fluctuations (apparition/ disparition erratique de composantes) qui surviennent lorsqu'une composante a une amplitude proche de la valeur du seuil.

Nous appliquerons un filtre récursif du second ordre pour limiter l'évolution temporelle dans chaque bande de fréquence analysée. Ceci permettra de limiter la rapidité d'apparition et de disparition de composantes spectrales (filtre passe-bas), de ne laisser passer que les sons qui répondent à certains critères d'évolution (filtre passe-bande), d'accentuer les sons transitoires (filtre passe-haut) et d'introduire des résonances qui se traduiront par des oscillations de l'intensité de chacune des composantes spectrales. Remarquons qu'il s'agit là d'un type de transformation très différente de l'application d'un filtre résonant dans le domaine temporel. Nous n'avons à ce jour trouvé aucun article mentionnant une telle technique et nous en ferons écouter des exemples sonores.

2.7.2. Prise en compte des bandes fréquentielles adjacentes

Les fonctions de seuils pourraient également être appliquées tant à la bande fréquentielle qui remplit la condition, qu'aux bandes fréquentielles adjacentes.

Et le critère de décision lui-même pourrait dépendre des bandes adjacentes. Il s'agirait en quelque sorte d'une opération de détection de pics. On pourrait ainsi accentuer ou réduire les résonances des signaux, à la fois en amplitude et en largeur de bande, voire les déplacer.

Une autre voie de recherche consiste à utiliser un filtre sur le spectre comme s'il s'agissait d'un signal temporel. De cette manière, on créerait une sorte de "flou" fréquentiel qui produirait probablement un effet de choeur. Il est difficile d'imaginer le résultat sonore, surtout si l'on introduit un facteur de résonance, mais l'effet sera à coup sûr totalement nouveau.

2.7.3. Extension des modifications de l'axe des fréquences

Amélioration des fonctions de transposition et de décalage fréquentiel à l'aide de tables d'arctangentes et introduction de modifications non linéaires de l'axe fréquentiel afin de créer des inharmonicités locales dans le son.

3. Modules de filtrage: breakpt_filter~ et band_filter~

Le module breakpt_filter~ génère un gabarit de filtrage formé de segments de droites (breakpoint) reliant un nombre variable de points (fréquence, amplitude) ainsi que l'on le découvre à la figure 3.

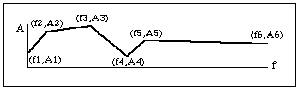
Figure 3 : Gabarit de filtrage généré par breakpt_filter~.

Le module band_filter~ génère un gabarit de filtrage formé de segments de droites horizontales en fonction d'un nombre variable de points (fréquence, amplitude) ainsi que l'on le découvre à la figure 4.

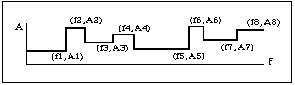
Figure 4 : Gabarit de filtrage généré par band_filter~ .

Ils permettent notamment de réaliser toutes les fonctionnalités d'un égaliseur graphique dont les fréquences centrales et les amplitudes sont modifiables en temps réel à l'aide d'un boîtier de potentiomètres MIDI (voir figure 5).

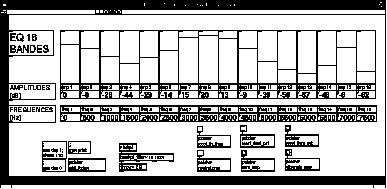
Figure 5 : Exemple de patch MAX réalisant un égaliseur graphique.

Une autre application consiste à interpoler entre plusieurs fonctions de transfert, à l'aide de l'application Circ.app développée par Gerhard Eckel à l'IRCAM. Nous avons utilisé les objets "table" standards de Max afin de dessiner quatre gabarits de filtre. Le gabarit résultant est interprété par breakpt_filter~ avant d'être envoyé au module d'analyse-synthèse (voir figure 6). Cette expérience a permis de valider l'intérêt de la méthode et nous écrirons des modules externes afin d'autoriser des variations plus rapides. Des procédures de variation dynamiques, éventuellement liées à des modifications des caractéristiques du signal d'entrée, permettront de créer un vie interne intéressante dans les sons.

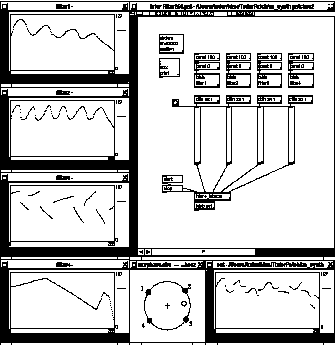
Figure 6 : Exemple d'interpolation entre plusieurs gabarits.

4. Module de filtrage: peak_filter~

Ce module génère un gabarit de filtrage formé d'un nombre variable de pics définis chacun par sa fréquence, son amplitude et sa largeur de bande, ainsi que l'on le découvre à la figure 7. Il permet de localiser un certain nombre de résonances dans le spectre.

Tous les paramètres sont bien sûr modifiables en temps réel, que ce soit à l'aide d'un patch MAX ou à l'aide de tout système de commande MIDI.

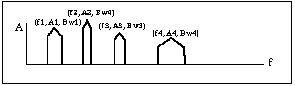
Figure 7: Gabarit de filtrage généré par peak_filter~ .

5. Module de lissage: cepstral_smooth~

Le calcul du cepstre consiste à effectuer une transformée de Fourrier du spectre d'amplitude logarithmique obtenu par analyse FFT du signal sonore. On obtient ainsi une nouvelle représentation du signal dans le domaine des "quéfrences". Les premiers coefficients décrivent grosso modo l'enveloppe du spectre d'amplitude logarithmique du signal de départ, tandis que les derniers coefficients décrivent sa structure harmonique. On peut modifier ces coefficients (généralement, en supprimer une partie), puis faire une FFT inverse afin d'obtenir un spectre d'amplitude logarithmique modifié. Il suffit alors de faire le calcul de l'exponentielle pour trouver un spectre d'amplitude linéaire. Ce signal, qui suit fidèlement le spectre d'un signal sonore de départ, sera envoyé à l'entrée gabarit du module d'analyse/synthèse principal.

La méthode du cepstre permet donc de lisser le spectre en fonction du nombre de paramètres conservés dans le domaine des "quéfrences" (voir figure 8).

Le nombre de points conservés peut être modifié en temps réel à l'aide de tout contrôleur MIDI. Il s'agit à notre connaissance du premier programme qui permette la variation de ce facteur de lissage en temps réel. Un certain nombre de transitions intéressantes sont ainsi rendues possibles, allant d'un spectre contenant la trace des harmoniques à une enveloppe plus ou moins lisse. Dans le cas de la synthèse croisée avec un son de voix (effet vocodeur analogique, mais avec une précision de loin supérieure: on passe d'une douzaine de filtres analogiques habituellement à 512 bandes de filtrage!), on peut moduler l'intelligibilité de la voix en direct et faire apparaître ou non les harmoniques du signal vocal.

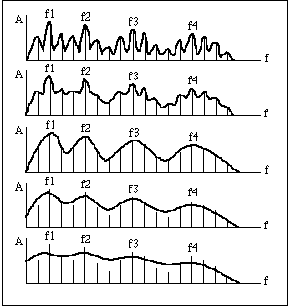
Figure 8 : De haut en bas, lissage progressif d'un signal de parole.

D'autre formes de transformations spectrales seront programmées prochainement. Il serait par exemple intéressant d'expérimenter divers algorithmes de modification des courbes d'enveloppes spectrales qui permettent par exemple d'accentuer ou d'atténuer les pics formantiques, mais aussi des transformations fréquentielles: transposition, décalage fréquentiel et modifications non linéaires de l'axe des fréquences (voir figure 9). Et des modifications dynamiques de ces facteurs de forme induiraient sans aucun doute des textures sonores mobiles nouvelles et intéressantes.

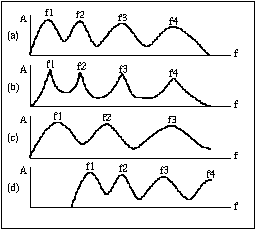
Figure 9 : Modification du spectre lissé: (a) original, (b) accentuation des résonances,

(c) transposition et (d) décalage fréquentiel.

6. Conclusions

Les résultats obtenus jusqu'ici sont concluants tant au niveau de la qualité sonore qu'au point de vue de l'étendue des possibilités de transformation rendues possibles par les nombreuses combinaisons de modules. Il est par exemple possible de réaliser, sur une seul carte ISPW-16, une analyse-synthèse à 1024 points avec un taux de recouvrement de 75%, en réalisant dans le domaine fréquentiel des opérations sur les seuils, tout en modifiant l'axe des fréquences et en combinant un égaliseur graphique avec une synthèse croisée à partir d'une enveloppe spectrale obtenue par lissage cepstral d'un signal auxiliaire.

Nous travaillons en ce moment sur les pistes que nous avons ébauchées et nous pensons être en mesure de proposer prochainement des traitements sonores nouveaux. Signalons également que des sons très intéressants peuvent être obtenus lorsque l'on travaille sur des signaux stéréo, mais deux cartes ISPW-16 sont alors nécessaires si l'on désire obtenir une qualité de traitement optimale.

Références

[Allen &Rabiner, 1977] J. B. Allen & Lawrence R. Rabiner, A Unified Approach to Short-Time Fourier Analysis and Synthesis, Proceedings of the IEEE, Vol. 65, No. 11, Novembre 1977, pp. 1558-1564.

[Depalle & poirot] Philippe Depalle & G. poirot, Super Vocodeur de Phase: A Modular System for Analysis, Processing and Synthesis of Sound Signals, Proc. ICMC 1991, pp. 161-164.

[Griffin & Lim, 1984] W. Daniel & Jae S. Lim, Signal Estimation from Modified Short-Time Fourier Transform, IEEE Trans. ASSP, Vol. 32, No. 2, Avril 1984, pp. 236-243.

[Portnoff, 1976] Michael R. Portnoff, Implementation of the Digital Phase Vocoder Using the Fast Fourier Transform, IEEE Trans. ASSP, Vol. 24, No. 3, Juin 1976, pp. 243-248.

[Portnoff, 1980] Michael R. Portnoff, Time-Frequency Representation of Digital Signals and Systems Based on Short-Time Fourier Analysis, IEEE Trans. ASSP, Vol. 28, No. 1, Février 1980, pp. 55-69.

[Serra, 1993] Marie-Helene Serra, Super Vocodeur de Phase: Introduction + SUper Vocodeur de Phase: Référence, Documentation IRCAM, Octobre 1993, 62 + 50 pages.

[Settel & Lippe, 1994] Zack Settel & Cort Lippe, Realtime Musical Applications using FFT based Resynthesis, Proceedings ICMC, Aarhus, 1994.

[Todoroff, 1995] Todor Todoroff, Instrument de synthèse granulaire dans Max/FTS, Proceedings ISEA, Montreal, 1995.

Recherche subventionnée en Belgique par la Région Wallonne.