Simulation of an analog audio circuit of a wah pedal:
a port-Hamiltonian approach

This page concerns the Port-Hamiltonian simulation of an analog audio circuit: the Dunlop Cry-Baby wah pedal.

Procedure and results will be presented at the 135th convention of the Audio Engineering Society

AES

AbstractAbstract

Several methods are available to simulate electronic circuits. However, for nonlinear circuits, the stability guarantee is not straightforward. In this paper, the approach of the so-called "Port-Hamiltonian Systems" (PHS) is considered. This framework naturally preserves the energetic behavior of elementary components and the power exchanges between them. This guarantees the passivity of the (source-free part of the) circuit.

After a short introduction of this tool, a PHS formulation of a Cry-Baby pedal circuit is derived in the continuous time domain. Second, a numerical scheme is specially designed so that a discrete-time version of the original power balance is satisfied. Then, a simulation is built. Results prove stable and in good accordance with LTSpice simulations.

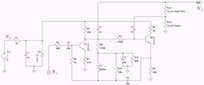
Schematic Schematic

Cry-Baby wah pedal Schematic

Results Results

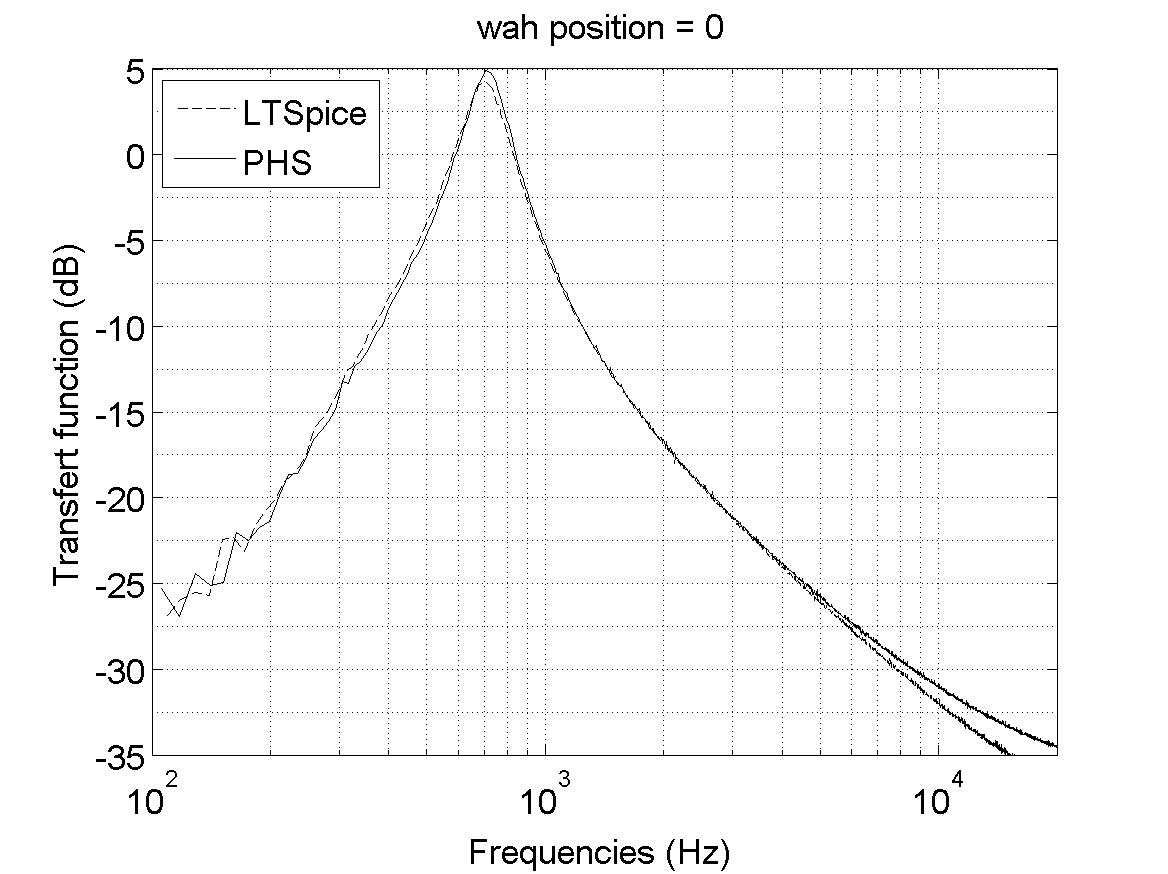
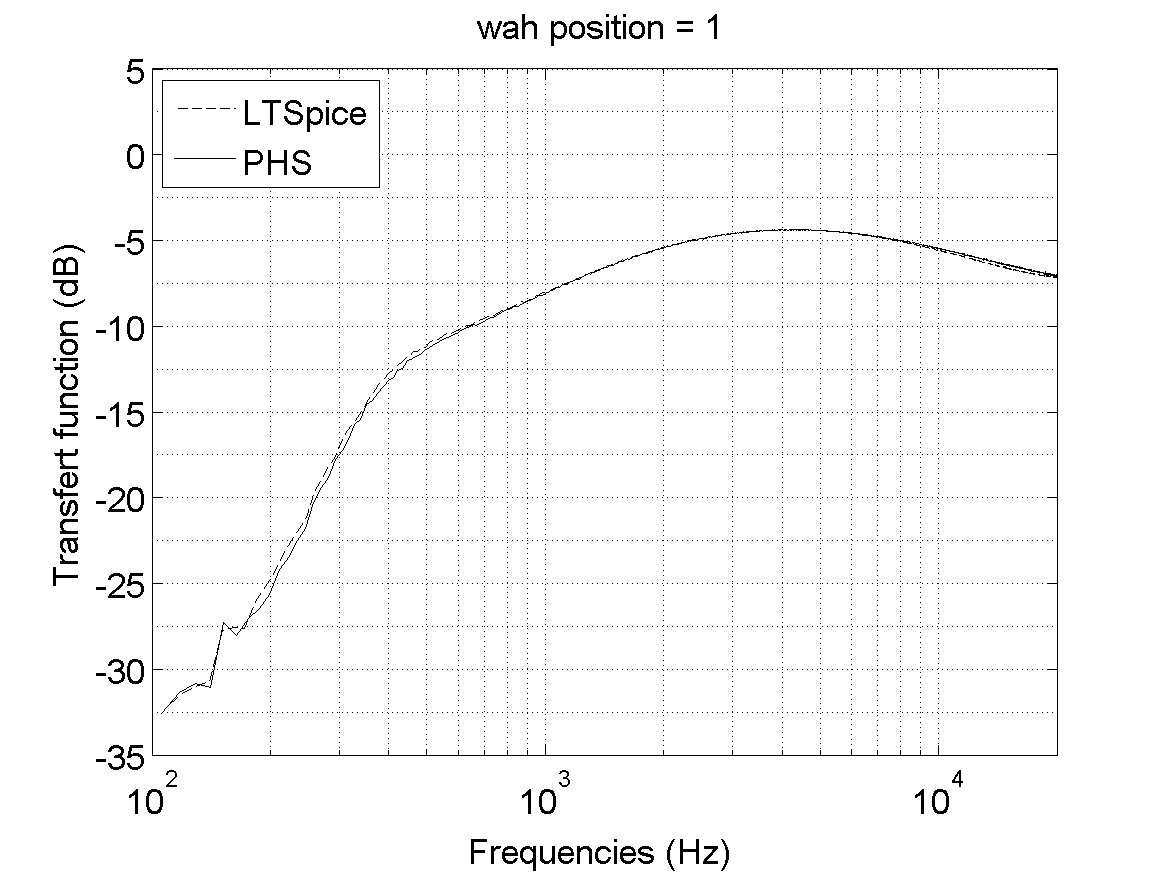
Wah position is 0 Wah position is 1

Comparison between the transfert functions of our PHS simulation
and LT-Spice simulation of the Cry-Baby.