We have presented two new closed forms for LIF and allpass delay filters applied to fractional delay filtering.
For LIFs, the Horner scheme leads to an efficient time varying
modular implementation which may decrease significantly the computing
cost relatively to the Farrow structure. Figures 2 and
3 show the modular implementation of 
.
Figure 2: Modular implementation of the fractional delay filter (see
figures 3 and 4 for details of modules
).
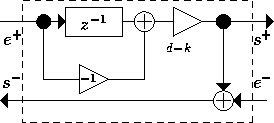
Figure 3: Module structure for the Lagrange Interpolation implementation.
Figure 4: Module structure for the continued fraction implementation.
It is also possible to deduce a modular implemention of a filter,
the transfer function of which is given as a continued fraction
expansion in 
. On figures 2 and
4, we show a way of implementing a filter which transfer
function is given by the following continued fraction:
The fractional part, 
(eq. 8), is obtained after
performing the following substitutions:
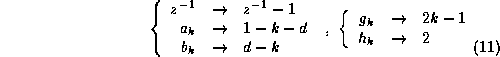
In our case, unfortunately this modular implementation
involves loops which include 
instead of
. From a computational point of view, these loops can not be
samulated since the output and the input of are to be
inextricably linked together. Thus this modular approach seems to be
usable only from a theoretical point of view.
