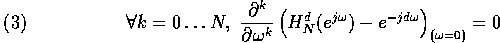Next: Recursive Expression for
Up: LAGRANGE INTERPOLATOR FILTER
Previous: LAGRANGE INTERPOLATOR FILTER
The LIF of order N consists in a FIR filter, 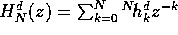 , where
, where 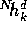 are parametrised by a
polynomial in d. The LIF has to correspond to an exact delay filter
when d is integer, which means that
are parametrised by a
polynomial in d. The LIF has to correspond to an exact delay filter
when d is integer, which means that 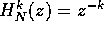 for k
between 0 and N. This leads to a system of linear equations whose
solution gives the impulse response (see [2]):
for k
between 0 and N. This leads to a system of linear equations whose
solution gives the impulse response (see [2]):

As pointed out in [4], it appears that any filter which
verifies the so called maximally flat condition (eq. 3)
is a LIF. Said differently it means that the LIF corresponds to the FIR
filter whose Fourier transform best fits the ideal Fourier transform
at the zero frequency.
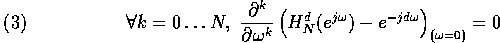
TASSART Stephan
Sat Apr 6 13:58:45 EET DST 1996
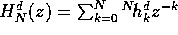 , where
, where 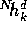 are parametrised by a
polynomial in d. The LIF has to correspond to an exact delay filter
when d is integer, which means that
are parametrised by a
polynomial in d. The LIF has to correspond to an exact delay filter
when d is integer, which means that 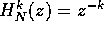 for k
between 0 and N. This leads to a system of linear equations whose
solution gives the impulse response (see [2]):
for k
between 0 and N. This leads to a system of linear equations whose
solution gives the impulse response (see [2]):