

Next: RBF neural networks
Up:
Neural networks for
Previous: Introduction
Assume an n-dimensional dynamical system 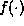 evolving on an
attractor A. A has fractal dimension d, which often is
considerably smaller then n. The system state
evolving on an
attractor A. A has fractal dimension d, which often is
considerably smaller then n. The system state 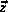 is observed
through a sequence of measurements
is observed
through a sequence of measurements 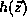 , resulting in a time
series of measurements
, resulting in a time
series of measurements 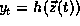 . Under weak
assumptions concerning
. Under weak
assumptions concerning 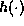 and
and 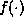 the fractal embedding
theorem[Sauer et al. ,
1991] ensures that, for
the fractal embedding
theorem[Sauer et al. ,
1991] ensures that, for 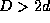 , the
set of all delayed coordinate vectors
, the
set of all delayed coordinate vectors
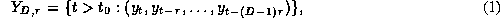
with an arbitrary delay time  and arbitrary
and arbitrary 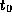 , forms an
embedding of A in the
, forms an
embedding of A in the 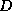 -dimensional reconstruction space.
We call the minimal
-dimensional reconstruction space.
We call the minimal 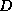 , which yields an embedding of A, the
embedding dimension
, which yields an embedding of A, the
embedding dimension 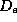 . Because the embedding preserves
characteristic features of A, it may be employed for building a
system model.
. Because the embedding preserves
characteristic features of A, it may be employed for building a
system model.
In the case of instationary systems the concept of attractors,
which does rely on the behavior of the system for 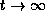 , does
not take over immediately. If, however, the instationarity is due to
slowly varying system parameters, it is possible to model the system
dynamics using a sequence of attractors. As it turns out this
approach leads to reasonable results in the case of musical instruments.
, does
not take over immediately. If, however, the instationarity is due to
slowly varying system parameters, it is possible to model the system
dynamics using a sequence of attractors. As it turns out this
approach leads to reasonable results in the case of musical instruments.
Axel Roebel
Mon Jul 31 15:37:17 MET DST 1995
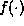 evolving on an
attractor A. A has fractal dimension d, which often is
considerably smaller then n. The system state
evolving on an
attractor A. A has fractal dimension d, which often is
considerably smaller then n. The system state 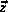 is observed
through a sequence of measurements
is observed
through a sequence of measurements 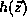 , resulting in a time
series of measurements
, resulting in a time
series of measurements 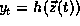 . Under weak
assumptions concerning
. Under weak
assumptions concerning 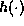 and
and 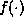 the fractal embedding
theorem[Sauer et al. ,
1991] ensures that, for
the fractal embedding
theorem[Sauer et al. ,
1991] ensures that, for 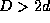 , the
set of all delayed coordinate vectors
, the
set of all delayed coordinate vectors
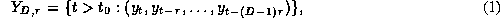
 and arbitrary
and arbitrary 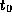 , forms an
embedding of A in the
, forms an
embedding of A in the 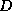 -dimensional reconstruction space.
We call the minimal
-dimensional reconstruction space.
We call the minimal 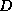 , which yields an embedding of A, the
embedding dimension
, which yields an embedding of A, the
embedding dimension 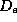 . Because the embedding preserves
characteristic features of A, it may be employed for building a
system model.
. Because the embedding preserves
characteristic features of A, it may be employed for building a
system model.
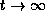 , does
not take over immediately. If, however, the instationarity is due to
slowly varying system parameters, it is possible to model the system
dynamics using a sequence of attractors. As it turns out this
approach leads to reasonable results in the case of musical instruments.
, does
not take over immediately. If, however, the instationarity is due to
slowly varying system parameters, it is possible to model the system
dynamics using a sequence of attractors. As it turns out this
approach leads to reasonable results in the case of musical instruments.