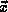There are different topologies of neural networks that may be used
for time series modeling. In our investigation we used radial basis
function networks. As proposed by Verleysen et. al
Verleysen/Hlavackova:94 we initialize the network using a
vector quantization procedure and then apply backpropagation training
to finally tune the network parameters. The tuning of the parameters
yields an improvement of factor ten in prediction error compared to
the standard RBF networks approach [Moody and Darken, 1989].
The resulting network function for m-dimensional vector valued output
and n-dimensional input vector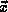 
is of the form
where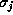 
stands for the standard deviation of the Gaussian,
the centers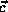 
are n-dimensional 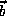and 
and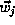 
are m-dimensional parameters of the network. Networks of the form
eq. (2) with a finite number of hidden units are able to
approximate arbitrary closely all continuous mappings 
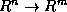[Park and Sandberg, 1991]. This universal approximation property is the
foundation of using neural networks for time series modeling, where
they are referred to as neural models.
To be able to represent instationary dynamics, we extend the network function to have an additional input t, that enables us the control of the actual mapping
From the universal approximation properties of the RBF-networks stated above it follows that eq. (3), with appropriate control sequence t, is able to approximate any sequence of functions. The control input sequence is used to discriminate between the different system attractors that generate the overall instationary dynamics. The control sequence may be optimized during training [Levin, 1993], or may be chosen a-priori fixed, in which case we have to ensure the discriminating behavior. For training the network it is necessary to supply enough training data for each of the generating attractors.
