

Next: Practical results
Up:
RBF Networks for
Previous: RBF neural networks
As is shown in figure 1 we use the delayed coordinate
vectors and a selected control sequence to train the network to
predict the sequence of the following TT time samples. The vector
valued prediction avoids the need for a further interpolation of the
predicted samples. The interpolation would be necessary to obtain the
original sample frequency, but, because the Nyquist frequency is not
regarded in choosing TT , is not straightforward to achieve.
After training we initialize the network input with the first input
vector 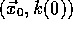 of the time series and iterate the network
function shifting the network input and using the latest output unit
to complete the new input. The control input may be copied from the
training phase to resynthesize the training signal or may be varied to
get emulate another sequence of system dynamics.
of the time series and iterate the network
function shifting the network input and using the latest output unit
to complete the new input. The control input may be copied from the
training phase to resynthesize the training signal or may be varied to
get emulate another sequence of system dynamics.
The question that arises in this context is the question of stability.
Due to the networks approximation errors the iterated model will soon
leave the attractor embedding. It is not guaranteed to stay close to
it because there is no training data in the neighborhood of the
attractor. Nevertheless, as we will see in the examples, the neural
models are stable for at least some parameters DD and TT . It may
be the case for other time series, however, that there exist no
parameters for stable models.
One method to increase the model stability is to use noisy input data,
thereby smoothing the prediction function in the surrounding of the
attractor. Due to the additional effect of higher prediction errors,
the overall effect is not always positive. Recurrent backpropagation
has been tried to learn some iterated prediction steps, but this did
not improve the results. The stability of the models is subject of
further research.


Next: Practical results
Up:
RBF Networks for
Previous: RBF neural networks
Axel Roebel
Thu Nov 9 12:55:11 MET 1995
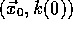 of the time series and iterate the network
function shifting the network input and using the latest output unit
to complete the new input. The control input may be copied from the
training phase to resynthesize the training signal or may be varied to
get emulate another sequence of system dynamics.
of the time series and iterate the network
function shifting the network input and using the latest output unit
to complete the new input. The control input may be copied from the
training phase to resynthesize the training signal or may be varied to
get emulate another sequence of system dynamics.