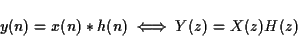3.1 Digital Signal Processing

This section will give a brief introduction to, and a formal definition of, the basic concepts and methods of the theory of digital signal processing used in this project. They form the basis for the methods presented in the subsequent chapters. Necessarily, this introduction will be very brief and restricted. In particular, I will consider the theory of digital signal processing apart from the more general theory of analog signal processing, and will pass over the various problems and mathematical prerequisites one has to take care of (stability, convergence). See [RH91] for a broad introduction, [Rob98] for an online tutorial, and [OS75] for a more profound presentation.

   
3.1.1 Sampling

The audio data we wish to treat will generally be present in the form of electric oscillations. These can either come from a microphone recording acoustic sound waves, from a tape, or an electronic instrument or device. To convert these oscillations to a form that can be treated by a computer they have to be digitised, i.e. reduced from an analog form (time- and value-continuous) to digital (time- and value-discrete). This process is called A/D conversion  or sampling . It consists of two steps:

1.

First, the analog signal s(t) is converted to a time-discrete form x(n) by sampling its value (in the more specific sense of the word) in periodical intervals of duration t_s, the sampling period , (see figure 2.1). The sampling rate  is then defined as:

The index n of the sampled signal x(n) is related to time by t = nt_s such that

x(n) = s(nt_s)

2.

Then, the value-continuous samples are rounded to yield a value-discrete binary number, commonly called a sample . For most commercial audio applications, a 16 bit integer format is used, for research, however, a normalized 32 bit floating point format with values ranging from -1.0 to 1.0 is preferred. This step 2 is called quantization  (see figure 2.2).

  

Figure 2.1: Conversion of an analog to a time-discrete signal ( sampling)

  

Figure 2.2: Conversion of a time-discrete to a digital signal ( quantization)

The result of A/D conversion is shown in figure 2.3. It is a curve with discrete steps at every sample. Note, however, that for most of the theory of digital signal processing, as for the rest of this chapter, the samples are generally considered to be value-continuous.

  

Figure 2.3: Result of A/D conversion

There are various sources of errors in the process of A/D conversion, including jitter, quantization noise, and aliasing:

Jitter

Deviations of the periodicity of the sampling of the analog signal (step 1 above) are called jitter . Jitter is a technical problem that is solved with current technology.

Quantization noise

Because of the rounding errors in the process of quantization (step 2 above), quantization noise  is introduced into the sampled signal. The rounding errors are dependent of the number of quantization intervals, i.e. the number of values D one sample can express. Because a sample is stored as a binary number, D has the form 2ⁿ, with n being the number of bits (the word length ) of the binary number. As a rough estimate, the ratio between the signal and the quantization noise increases by 6 dB per bit added (see section 2.1.2 for a definition of the unit dB).

Aliasing

According to the sampling theorem  of Nyquist , the sampling frequency f_s must be at least twice the highest frequency occurring in the signal. ^3.1 If not, the parts of the signal above f_s / 2 are introduced as low frequency aliasing noise  in the sampled signal. To avoid this, an anti-aliasing filter  is inserted before the A/D converter to suppress frequencies above half of the sampling frequency.

Converting a digital signal back to an analog signal is called D/A conversion . Roughly, it consists of reading the samples and generating an electric oscillation accordingly. As this will look like the step-curve in figure 2.3, it has to be smoothed by a low-pass filter (a filter that lets only the frequencies below his cutoff-frequency pass) to yield a signal suitable to being amplified and played via loudspeakers, or recorded on analog tape.

   
3.1.2 Power and Energy

The notion of energy and power for digital signals is only slightly related to the physical units pertaining to analog electrical signals. They are, nevertheless, related to the perceived loudness, albeit in a non-trivial way.^3.2

The power  of a signal x(n) is defined by

Then its energy  is

Taken as such, this value doesn't tell us much. It is useful, however, to compare two signals. For this end, the unit decibel  (dB) is introduced: The ratio R in dB of two signals with energies E₁and E₂ is

$$R = 10 \* \log_{10} \frac{E_1}{E_2}$$

Often, however, an implicit reference energy of E₂ = 1 is used. A ratio of 10 dB corresponds roughly to doubling the loudness. The unit decibel is well suited to practical use, since the dynamic range of the human ear is quite large, still, the values in decibel stay in a manageable range. For example, if the threshold of hearing is defined as a reference point of 0 dB, the dynamic range reaches up to 120 dB, the pain threshold. This corresponds to doubling the loudness 12 times.

3.1.3 Fourier Transform

After A/D conversion, the signal x(n) is represented in the time domain as a sequence of numbers. According to Fourier's ingenious idea , any function, even nonperiodic ones, can be expressed as a sum of (periodic) sinusoids (which can not be further decomposed, i.e. they are ``pure'' ^3.3 ). In the complex domain, a sinusoid can be expressed by

$$e^{j\omega n} = \cos \omega n + j \sin \omega n$$

with the angular frequency  $\omega$ given by

$$\omega = \frac{2\pi}{N} k$$

for some discrete frequency k and N frequency bands, or, related to frequencies in Hertz  (Hz), as

$$\omega = \frac{2\pi}{f_s} f$$

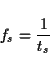
So, to reveal the frequency structure of x, it can be converted to a frequency domain representation X by the discrete Fourier transform  (DFT):

   $$X(k) = \sum_{n=0}^{N-1}{e^{j\frac{2\pi}{N}nk}x(n)}$$

X is called the frequency spectrum  of the digital signal xof length N. To go the other way, we use the inverse discrete Fourier transform :

   $$x(n) = \frac{1}{N} \sum_{k=0}^{N-1}{e^{-j\frac{2\pi}{N}nk}X(k)}$$

The result of the Fourier transform in (2.9) is N complex numbers X(k) which define the magnitude spectrum  M(k) and phase spectrum  $\phi(k)$ for a discrete frequency k:

  

$$\left\vert X(k) \right\vert$$ M(k) = (3.1)

$$\phi(k) \angle X(k) = \arctan \left\vert \frac{\makebox[3.5ex]{\textbf{re\hfill}} X(k)}{\makebox[3.5ex]{\textbf{im\hfill}} X(k)} \right\vert$$ = (3.2)

The magnitude spectrum gives the intensity of a sinusoid at frequency k, while the phase spectrum gives its shift in time. Often, the phase spectrum is ignored (it is not important for speech recognition), and the term Fourier spectrum or spectrum is used for the magnitude spectrum.

There exists a generalization of the discrete Fourier transform ^3.4, called the Z-transform , which often simplifies the representations in the frequency domain. The Z-transform X(z) of a discrete sequence x(n), where z is a complex variable, is defined as:

$$X(z) = \sum_{n=-\infty}^{\infty}{x(n)z^{-n}}$$

If z is substituted by 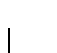$e^{j\omega k}$, the relationship to the Fourier transform is obvious. See [OS75] for a rigorous presentation of the Z-transform, or [Mel97] for an on-line tutorial.

The computational complexity of the DFT, when computed directly, is O(N²). By taking advantage of the periodicity of the analysing sinusoid $e^{-j\frac{2\pi n}{N} k}$ and applying the divide and conquer  principle of splitting the problem into successively smaller subproblems, a variety of more efficient algorithms of complexity $O(N \log N)$ have been developed which came to be known collectively as the fast Fourier transform  (FFT). They generally require that Nbe a power of two. As the discrete Fourier transform and its inverse differ only in the sign of the exponent and a scaling factor, the same principles lead to the inverse fast Fourier transform  (IFFT).

3.1.4 Convolution, Filtering and Linear Systems

The fundamental operation of digital signal processing is the convolution  of two signals x(n) and h(n) to yield y(n), defined by

$$y(n) = x(n) * h(n) := \sum_{k=-\infty}^\infty {x(k) h(n-k)}$$

  

Figure 2.4: Convolution of a discrete signal x(n) with a signal h(n).

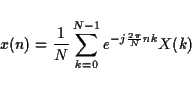
This is what is behind the notion of filtering : The output signal y is x filtered by h. It is usually expressed graphically as shown in figure 2.4. This operation is commutative and associative:

  

x(n) * h(n) = h(n) * x(n) (3.3)

h₁(n) * (h₂(n) * x(n)) = h₂(n) * (h₁(n) * x(n)) = (h₁(n) * h₂(n)) * x(n) (3.4)

Systems which perform linear operations such as convolution, addition, and multiplication by a constant are part of the class of linear time-invariant systems   (LTI systems ). ^3.5 They are notated as in figure 2.5.

  

Figure 2.5: A linear time-invariant system performing operation T.

The properties of linearity  and time-invariance  are defined as:

T [ a x₁(n) + b x₂(n) ] = a T [x₁(n)] + b T [x₂(n)] (3.5)

$$\iff y(n-k) = T [x(n-k)] \qquad \textrm{for all\ } k \in {\bf Z}$$ y(n) = T [x(n)] (3.6)

As a consequence, an LTI system is completely defined by its impulse response  h(n), which is the output of the system to a single unit impulse  $\delta(n)$ with

   $$\delta(n) = \left\{ \begin{array}{ll} 1 & \qquad \textrm{... ... 0 \\ 0 & \qquad \textrm{for\ } n \ne 0 \end{array} \right.$$

An important property is that a convolution of two signals in the time-domain can be expressed by a multiplication of their spectra in the frequency-domain. If X, Y and H are the Z-transforms of x, y and h, then

$$y(n) = x(n) * h(n) \iff Y(z) = X(z) \* H(z)$$

This is expressed in figure 2.6. The Fourier transform H(z) of the impulse response h(n) of a filter is called the transfer function  of the filter.

The above provides the link between the intuitive notion of filtering as a selective attenuation or amplification of certain frequencies in a signal to the mathematical operations of convolution and Fourier transformation.

  

Figure 2.6: Filtering in the frequency-domain.

   
3.1.5 Windowing

So far, we have considered the signal as a whole, even if it was of infinite length. For practical applications, and in order not to lose all time information in the transition to frequency domain, small sections of the signal of about 10-40 ms are treated one at a time. These small sections are called windows  or frames  . To avoid introducing artefacts into the frequency-domain, caused by discontinuities at the borders of the window, the signal is first multiplied by a window function  w(n), which provides for a smooth fade-in and fade-out of the window.

x_w(n) = x(n) w(n)

The windowed signal x_w(n) is then converted by the Fourier transformation. The windows are usually placed so that they overlap (see figure 2.7).

  

Figure 2.7: Overlapping Hamming windows

In the following, the formulas and graphs of some of the most widely used window functions are shown, together with the magnitude spectra of a signal consisting of two sinusoids at different frequencies and amplitudes, multiplied by the corresponding window function. These spectra show the distortion or smear that is introduced by the window function. Ideally, there would be only two sharp peaks.

Rectangle

  (figure 2.8)

$$w(n) = \left\{ \begin{array}{ll} 1 & \qquad \textrm{for} \qu... ... n < N \\ 0 & \qquad \textrm{otherwise} \end{array} \right.$$

 

Bartlett

  or triangular window (figure 2.9)

$$w(n) = \left\{ \begin{array}{ll} n \frac{2}{N-1} & \qquad \... ...\textrm{for} \quad \frac{N-1}{2} < n < N \end{array} \right.$$

 

Hamming

  (figure 2.10)

$$w(n) = 0.54 - 0.46 \cos \frac{2 \pi n}{N-1}$$

 

Hanning

  (figure 2.11)

$$w(n) = 0.5 - 0.5 \cos \frac{2 \pi n}{N-1}$$

 

Blackman

  (figure 2.12)

 

Gauss

  (figure 2.13)