4.2 LPC Spectral Envelope

LPC (linear predictive coding , see [MG80,Opp78,Rob98]) is an early method of digital signal processing, developed originally for speech transmission and compression. By the special properties of the method, it can also be used for spectral envelope estimation.

The idea behind LPC analysis  is to represent each sample of a signal s(n) in the time-domain by a linear combination of the ppreceding values s(n - p - 1) through s(n - 1). p is called the order  of the LPC. The approximated value $\hat{s}(n)$ is computed from the preceding values and ppredictor-coefficients  (also called LPC-coefficients ) a_i as follows:

$$\hat{s}(n) = \sum_{i=1}^{p} {a_i \: s(n-i)}$$

Now, for each time-frame, the coefficients a_i will be computed such that the prediction error $e(n) = \hat{s}(n) - s(n)$ for this window is minimal. For transmission, it is sufficent to send the p coefficients and the residual signal e(n), which uses a smaller range of values and can thus be coded with fewer bits. The receiver can easily recover the original signal from e(n)and the a_i.

  

Figure 3.1: LPC-analysis and synthesis for transmission

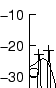
Transmitter and receiver can also be regarded as a linear system with an adaptive filter, as shown in figure 3.1. What happens when the residual signal e(n) is minimized, is that the analysis filter  with a transfer function given by

$$A(z) = 1 - \sum^p_{i=1} {a_i z^{-1}}$$

tries to suppress the frequencies in the input signal s(n) that have a high magnitude, in order to achieve a maximally flat spectrum (this is sometimes call whitening  of a spectrum). The synthesis filter  on the receiving side is the inverse of the analysis filter: It amplifies the frequencies that have been attenuated by the transfer function of the analysis filter

   $$\frac{1}{A(z)} = \frac{1}{1 - \sum^p_{i=1} {a_i z^{-1}}}$$

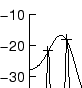
As can be seen, the synthesis filter 1/A(z) is an all-pole filter , since its transfer function is defined by a rational function with no zero points in the numerator, but with p zero points in the denominator A(z). Because these zero points come in compex-conjugate pairs, the absolute value (the magnitude) of the transfer function of the resulting filter shows p/2 poles , or peaks.

As the analysis filter tries to flatten the spectrum, it will adapt to it in a way that its inverse filter will describe the spectral envelope of the signal. As the order decreases (i.e. fewer poles are available), the approximation of the spectral envelope will become coarser, but the envelope will nevertheless reflect the rough distribution of energy in the spectrum. This can be seen in figure 3.2.

 

tex2html_comment_mark>

For the actual evaluation of the predictor-coefficients to minimize the prediction error, two classes of methods exist: the autocovariance method  and the autocorrelation method . Both have their advantages and disadvantages [Opp78], however, the autocorrelation method is more widely used, since it can be efficiently implemented using the Durbin-Levinson recursion . I won't elaborate on the methods here, since they are amply described in the literature.

In the course of evaluation of the predictor-coefficients, an intermediate set of parameters, the reflection coefficients  k_i are obtained, which, in fact, correspond to the reflection of acoustic waves at the boundaries between successive sections of an acoustic tube, as presented in section 2.4. These coefficients have advantages for synthesis, and can be interpolated without problems for the validity (stability) of the resulting synthesis filter.

Various other parameter sets exist [MG80,Rob98]: the roots of the analysis filter  A(z), log area ratios  (LAR ), the logarithm of the ratios of the areas of the sections of the acoustic tube model given by $\frac{A_{i+1}}{A_i} = \frac{1 - k_i}{1 + k_i}$, the line spectral pairs , and others. Since it is possible to convert between them, they don't need to be considered separately for representation.

 

tex2html_comment_mark>

Disadvantages of the LPC method

A disadvantage of the LPC spectral envelope in analysing harmonic sounds (sounds with a prevalent partial structure) is that it will tend to envelope the spectrum as tightly as possible, and will under certain conditions descend down to the level of residual noise in the gap between two harmonic partials. This will happen whenever the space between partials is large, as in high pitched sounds, and when the order is high enough, i.e. there are enough poles to come to lay on every partial peak. See figure 3.3 for an example of this effect.