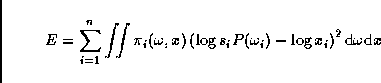5.4 Geometric Representation

Starting from a spectral representation, a geometrical representation can be derived, which tries to describe the amplitude curve of the spectral envelope in the frequency-domain with fewer points not spaced at equidistant frequencies. The geometrical representation can be of the form of a break-point function or splines, as described in the following.

  

Figure 4.1: Geometric representations of spectral envelopes: as a break point function (left); as splines with dashed continuous slope (right)

Break point functions

 A break point function  (BPF) is a general method of representing a function, be it in time- or frequency-domain. It consists of n break points  P_i at (x_i, y_i). In our case, x_i is the frequency and y_i the amplitude. The n-1 segments between the break points are interpolated linearly, as in figure 4.1, left.

Splines

 Splines  [UAE93] are similar to break point functions, but they provide for quadratic or cubic interpolation of each section between the points P_i given, using a polynomial of degree 2 or 3. Additionally, continuity constraints at the given points stipulate that the slope be identical. This slope (the dashed line in figure 4.1, right) can also be accessible as a parameter for manipulation.

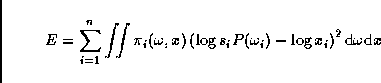Splines would be applied to spectral envelope representation in a way that the points P_i would be placed on the maxima and minima of the spectral representation, where the slope is zero, and on the turning points, where the curvature changes direction.

A weak general point of geometric representations is that they don't model the spectral envelope in a way relevant to its properties as a signal, but simply as a curve in euclidian space. Especially interdependencies between the given points, that arise from the signal character of the spectral envelope are not taken into account automatically. ^5.2

The stability of geometric representations is seriously disturbed by the fact that small changes can cause a sudden change of the maxima found. They are quite local, and can be made more so by adding points manually. They are flexible and easy to manipulate and will always give nice smooth curves. However, there is a tradeoff between ease of manipulation and preciseness: If there is a point that governs a large area that can thus be manipulated easily, the preciseness can suffer because a large stretch of the curve will be interpolated.

Regarding speed, the geometric representations are slightly more costly in synthesis than spectral representation. For splines, the evaluation of the interpolating polynomials have to be taken into account. The space needed is less than for spectral representation, even more so if pruning of redundant points can be applied (again at the cost of preciseness).

For specifying spectral envelopes manually by drawing, geometric representations are very well suited.