L'utilisation d'une non-linéarité est une autre
méthode pour générer des partiels à partir d'une sinusoïde. Il est
naturel de tenter de contrôler les partiels générés en utilisant les
relations de transformations trigonométriques. Les polynômes de
Chebyshev 
permettent en l'occurence de
transformer les expressions trigonométriques. Ils sont définis par la
relation de récurence suivante:
La propriété qui permet de transformer les expressions trigonométrique est la suivante:
Maintenant considérons le filtre non-linéaire qui associe à
l'entrée e la sortie s par la relation 
. D'après la
relation précédante, il apparaît qu'excité par une sinusoïde
d'amplitude unitaire, le filtre génère une autre sinusoïde de
fréquence k fois plus élevée.
Par contre évidemment la relation précédante n'est pas linéaire, et on ne peut pas la généraliser pour des sinusoïdes non unitaires. Par exemple pour le cinquième ordre, on a:
Cette relation montre que la répartition d'énergie entre les partiels dépend essentiellement de l'amplitude du signal en entrée. Pour des faibles amplitudes, le filtre se comportement linéairement et ne génère pas de partiels. Pour des valeurs d'amplitude supérieures, les harmoniques 3 et 5 apparaissent progressivement. En conséquence cette technique apporte un contrôle relativement simple du timbre directement par l'intermédiaire du niveau d'entrée du filtre.
Il est également possible d'intermoduler deux sinusoïdes. Similairement au cas de la synthèse par modulation de fréquence, cette opération génère des partiels aux fréquences multiples entières de celles présentes dans le signal original:
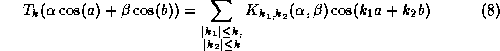
Toutefois, dans le cas général, il est compliqué d'exprimer
explicitement. Le contrôle reste
complexe. De plus, il n'existe pas de méthodes convaincantes d'analyse
de signaux pour ce modèle.