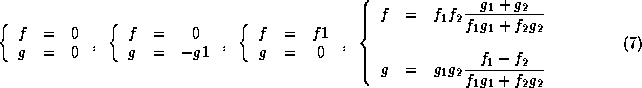
Le nouveau système d´equation est couplé, mais cela ne pose pas de problèmes particuliers. On définit chacun des systèmes par:
> lapin := {diff(f(t),t) = r*f(t)*(1-f(t)/f1-g(t)/g2),f(0)=f0};
> lynx := {diff(g(t),t) = g(t)*(-1-g(t)/g1+f(t)/f2),g(0)=g0};
> sys := lapin union lynx;
> F:=dsolve(subs(r=1.6,g2=5000,g1=25000,f2=1000,f1=100000,f0=38195,g0=200,sys),
{f(t),g(t)},numeric);
> plot({'subs(F(x),f(t))','subs(F(x),g(t))'},x=0..20);
L'équilibre est caractérisé par l'anullation des quantités f'(t) et g'(t), ce qui nous donne:
> solve(eval(subs(diff=0,g(t)=g,f(t)=f,f(0)=f0,g(0)=g0,sys)),{f,g,f0,g0});
Ce qui donne:
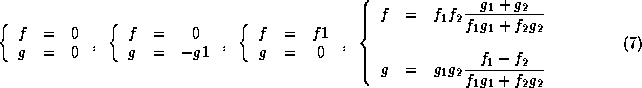
En l'occurence, une application numérique donne:
> op(evalf(subs(g2=5000,g1=25000,f2=1000,f1=100000,{"})));
![]()
On remarque toutefois que le système est pseudo-oscillant, de période à peu près 6 ans.