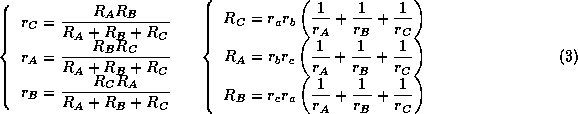La résistance équivalente du second schéma est 
alors que
la résistance équivalente du premier schéma est 
. Ce qui implique la relation suivante:
> eq1 := 1/(rA + rB) = 1/RC + 1/(RB+RA);Par permutation circulaire, on obtient les deux relations suivantes:
> eq2 := 1/(rB + rC) = 1/RA + 1/(RC+RB); > eq3 := 1/(rC + rA) = 1/RB + 1/(RA+RC);
Pour obtenir 
, 
, 
en fonction de 
, 
, 
,
il suffit de faire:
> solve({eq1,eq2,eq3},{rA,rB,rC});
Réciproquement, pour obtenir , , en fonction de ,
, , il suffit de faire:
> solve({eq1,eq2,eq3},{RA,RB,RC});
