Fonction carrée

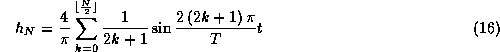
La même procédure permet d'obtenir les résultats suivants:

> a := (int (-1*cosphi, t=-T/2..0) + int (1*cosphi, t=0..T/2))*2/T;
> b := (int (-1*sinphi, t=-T/2..0) + int (1*sinphi, t=0..T/2))*2/T;
> simplify(subs(sin=0,cos(k*Pi)=(-1)^k,b));

On constate donc que les coefficients sont tous nuls, et que les coefficients valent . Si k est pair, alors vaut 1 et b est nul. Si k est impair, alors vaut -1 et b vaut . Donc la fonction carrée se décompose en série de Fourier celon:

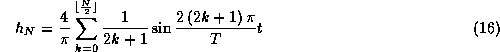
Pour obtenir le tracé des sommes partielles successives superposées à la fonction carrée:

> hh:=4/Pi*Sum( 1/(2*k+1)*sin(2*Pi*(2*k+1)/T*t),k=0..N);
> plot({'x->if x>0 then 1 else -1 fi'(t), 
        subs(T=1,N=10,hh)},t=-1/2..1/2);