Le tracé de la fonction triangle s'obtient en utilisant la fonction
[plot]:
> plot(t,t=-1/2..1/2);
Pour obtenir les coefficients de Fourier de la fonction triangle, il suffit d'expliciter les intégrales suivantes:
> a:=int( t * cosphi, t=-T/2..T/2) *2/T; > b:=int( t * sinphi, t=-T/2..T/2) *2/T;
La première intégrale est nulle, donc les coefficients 
sont bien
tous nuls. La seconde donne:
.
Comme k est entier, 
et
.
> simplify(subs(sin=0,cos(k*Pi)=(-1)^k,b));
Ce qui nous permet d'écrire la décomposition suivante:
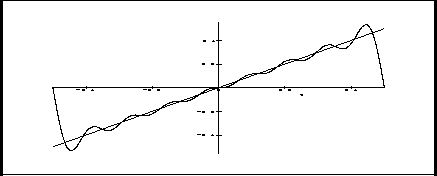
Figure 2: Décomposition en série de Fourier d'une fonction triangle
La superposition des deux courbes s'obtient alors de la façon suivante:
> gg:=-T/Pi*Sum( (-1)^k/k*sin(2*Pi*k/T*t),k=1..N);
> plot({t,subs(T=1,N=8,gg)},t=-1/2..1/2);