La décomposition en série de Fourier correspond mathématiquement à la
projection orthogonale d'une fonction complexe périodique de période
T sur le sous-espace vectoriel généré par la famille des fonctions
périodiques 
. La définition du produit
scalaire est la suivante:
La famille des est définie par:
alors
[int].
[int].
Les relations précédantes montrent que la famille est une famille de orthogonale, et par conséquent forme
une base orthogonale du sous-espace vectoriel engendré par
. Donc la décomposition en série de
Fourier de toute fonction périodique de période T, est décrite
par l'ensemble des relations suivantes:
sous forme d'une intégrale.
L'utilisation courante des décompositions en série de Fourier concerne les fonctions à valeurs réelles. On obtient la version réelle des décompositions en série de Fourier en prenant la partie réelle de la version complexe, ce qui donne:
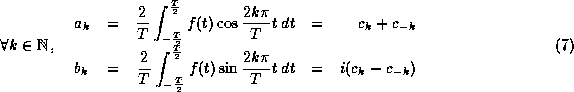
