On définit dans un premier temps l'expression proposée:
> hh:=4/Pi*Sum( 1/(2*k+1)*sin(2*Pi*(2*k+1)/T*t),k=0..N);Pour dessiner cette expression, par exemple, à l'ordre 6, il suffit de substituer N à 6 et T à 1:
> plot(subs(T=1,N=6,hh)},t=-1/2..1/2);
On a l'impression qu'en augmentant l'ordre du développement, les
fonctions tendent vers la fonction carrée qui correspond à la
périodisation de la fonction qui vaut -1 pour 
et 1 pour 
. On superpose la courbe limite avec la
somme partielle de la façon suivante:
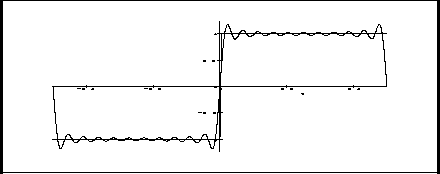
Figure 1: Décomposition en série de Fourier d'une fonction carrée
> plot({'x->if x>0 then 1 else -1 fi'(t),
subs(T=1,N=10,hh)},t=-1/2..1/2);